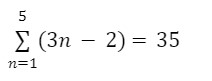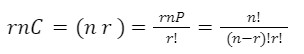Sequences and Series Notes
By the end of this chapter, you should be familiar with:
- Arithmetic sequence and series
- Sum of finite arithmetic sequences
- Geometric sequences and series
- Sum of finite and infinite geometric series
- Sigma notation
- The binomial theorem and the expansion of , ℕ
INTRODUCTION
Sequence- A sequence is a list of numbers that is written in a defined order, ascending or descending, following a specific rule. It can also be defined as a function whose domain is the set of positive integers. Ex. (1,2,6,8…), (1,4,9,16)
Series- A series is the the sum of all the terms in a sequence. However, there has to be a definite relationship between all the terms of the sequence. Ex. (1+2+6+8….), (1+4+9+16…)
A finite sequence has a fixed number of terms.
Ex. (6,12,18,24,30)
An infinite sequence has an infinite number of terms.
Ex. (3,9,27….3k,….)
The heights of consecutive bounces of a ball, compound interest, population growth and Fibonacci numbers are a few examples of sequences and series.
SEQUENCE
A term in a sequence is named using the notation a_n, where n is the position of the term in the sequence.
Ex. 1,2,4,6,8….
Then, a_1=1, a_2=2, a_3=4 and so on.
This sequence can also be described in function notation:
f(1)=1, f(2)=2, f(3)=4 and so on. (The domain as mentioned in previous section is Z+)
A formula or expression that mathematically describes the pattern of the sequence can be found for the general term, an.
Ex. Find the first 5 terms and the 50th term of the sequence – an = 2 – (1/n2)
We will simply put the values for n and find the required terms: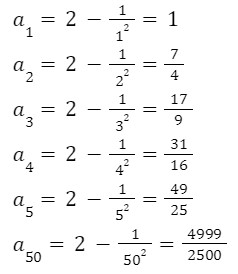
Ex. Find the first five terms for the following recursive sequences: an = 2an-1 -3 and a_1=1, n>1
First, put n=2 and replace the value of a1:
a2=2a1-3=2(1)-3=-1
Similarly, put n=3 and replace the value of a2:
a3=2a2-3=2(-1)-3=-5
Calculate a4 and a5 in the same fashion:
a4=2a3-3=2(-5)-3=-13
a5=2a4-3=2(-13)-3=-29
ARITHMETIC AND GEOMETRIC SEQUENCE
ARITHMETIC SEQUENCE
A sequence formed when each term after the first is found by adding a fixed non-zero number is called a arithmetic sequence.
The number which we add is called the common difference, denoted by d.
When d>0 the sequence is increasing
And when d<0 the sequence is decreasing.
Ex. 7,14,21,28,35,42…..
The terms in the sequence is 7 more than the preceding, in which case we can write:
an=a(n-1)+7, n>1
Here, 7 is the common difference (d).
Ex. 32,24,16,8,0,-8…..
The terms in the sequence is 9 less than the preceding, or we can say we add -9 to each term to get the next, we can write:
an=a(n-1)-9, n>1
Here, -9 is the common difference (d).
In general, we can write:
If a1,a2,a3,a4,…ak is a arithmetic sequence with d as the common difference, then:
a2=a1+d
a3=a1 + d + d =an1 + 2d
a4=a1+ 2d + d = a1+3d
and so on.
Looking at the pattern, we can write:
an=a1+(n-1)d
This formula is very useful in finding the terms of a sequence.
Ex. Find the 50th term of the sequence- 4,10,16,22…
It is clearly seen that the terms of the sequence are obtained by adding 6 to the preceding term. Therefore d=6, and we also have a1=4
Using the formula for nth term of an arithmetic sequence:
an=a1+(n-1)d
Putting n=50:
a50=4+(50-1)×6
a50=4+294
a50=298
Ex. Find an arithmetic sequence whose first term is 5 and fifth term is 11.
Using formula for nth term of an arithmetic sequence:
an=a1+(n-1)d
Putting n=5
a5=a1+4d
Given that a5=11 and a1=5:
11=5+4d
4d=6
d = 3/2
Putting the value of a_1 and d in the formula, we will get a general formula for the sequence: an = 5 + (3/2)(n-1)
GEOMETRIC SEQUENCE
A sequence in which every term is obtained by multiplying or dividing a non-zero number with the preceding number is known as a geometric sequence.
This non-zero number is called the common ratio (denoted by r).
When r>1, the sequence is diverging.
And when r<1, the sequence is converging.
Ex. 3,9,27,81…
The terms of the sequence are a product of 3 and the preceding term, so we say that 3 is the common ratio (r). We can also write: an=3a(n-1)
Ex. 64,32,16,8,4,2,1,1/2….
The terms in the sequence are obtained by dividing the preceding term by 2, so we say that 2 is the common ratio (r). We can also write: an = (1/2)an-1
In general, we can write:
If a1,a2,a3,…ak is a geometric sequence with common ratio r, then:
a2=ra1
a3=r(ra1 )=r2 a1
a4=r(r2 a1 )=r3 a1
and so on.
Looking at the pattern, we can write:
an=r(n-1) a1
This formula is very useful in finding terms of a geometric sequence.
Ex. Find the 6th term of the geometric sequence- 2,10,50,250…
It can be clearly seen that each term in the sequence is obtained by multiplying 5 to the preceding term. Therefore common ratio r=5 and we also have a1=2
Using the formula for finding terms in geometric sequence- an=r(n-1) a1
Putting n=6:
a6 = (5)5 x 2
a6=6250
Ex. In a geometric sequence a1=5 and a5=1280 and the last term of the sequence is 20480. Find the number of terms in the sequence. (r>0)
Using the formula for finding terms in geometric sequence- an=r(n-1) a1
Putting n=5, a1=5 and a5=1280:
a5 = r4a1
1280=r4×5
r4=256
r=4
Given that the last term is 20480, assuming n is the last term, then putting the values in the formula:
an=r(n-1) a1
20480=4(n-1) (5)
4(n-1)=4096
4(n-1)=46
n-1=6
n=7
There are seven terms in the geometric sequence.
SERIES
A series is the sum of terms in a sequence.
If a1,a2,a3,a4…an is a sequence, then Sn=a1+a2+a3…+an is a series.
A series can be written in a form called sigma notation.
Sn=a1+a2+a3…+an, can be written in sigma notation as:
Ex.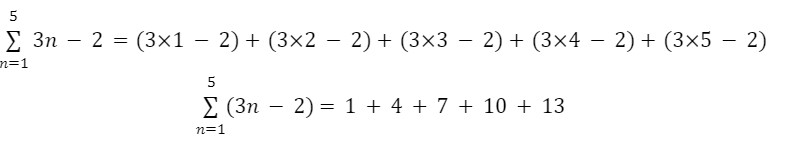
ARITHMETIC SERIES
Adding up the terms of an arithmetic sequence gives us arithmetic series.
Let’s see how we can calculate the sum of an arithmetic sequence:
Let a1,a2,a3,a4…an be an arithmetic sequence.
Then Sn=a1+a2+a3…+an is an arithmetic series. Now:
Let’s pair the terms in the summation in such a way, that the 1st term is paired with the last term, the 2nd term is paired with the second last term and so on:
Sn=(a1+an )+(a2+a(n-1) )+(a3+a(n-2) )+(a4+a(n-3) )+⋯
Now evaluating each pair:
(a1+an )=(a1 + an )
(a2+an-1 )= (a1 + d ) +(an – d ) = (a1 + an)
(a3+an-2 )= (a1 + 2d ) +(an – 2d ) = (a1 + an)
(a4+an-3 )= (a1 + 3d ) +(an – 3d ) = (a1 + an)
Looking at the pattern, we can say that all pairs are equal to (a1 + an)
There are n elements, therefore there will be n/2 such pairs, which makes the sum:
Sn=n/2(a1 + an)
Now, we know that an=a1+(n-1)d
Replacing the value of an: Sn = (n/2)(a1 + a2 + (n-1)d)
Sn = (n/2) (2a1 + (n-1)d)
Ex. Find the sum of first 30 terms of the series 9+13+17+21+…
Using the second formula –
Sn = (n/2)(a1 + + (n-1)d)
We have a1=9 and d=4
S30 = (30/2)(2(9) + (29)(4))
S30=15(18+116)
S30=2010
GEOMETRIC SERIES
Adding up the terms of an geometric sequence gives us arithmetic series.
Let’s see how we can calculate the sum of an geometric sequence:
Let a1,a2,a3,a4…an be an geometric sequence.
Then Sn=a1+a2+a3…+an is an geometric series. Now:
Let Sn=a1+a2+a3…+an ①
Multiply r in the equation ①
rSn = ra1 + ra2 + ra3….+ran We know that when r is multiplied to any term, we get the succeeding term, therefore:
rSn = a2 + a3 + a4….+ran ②
Now subtract ② from ①:
Sn-rSn= a1 -ran
Sn(1-r) =a1 – ran
Sn= (a1-ran)/(1-r)
Sn = (a1-ran)/(1-r) 𝒓 ≠ 1
We know that an=r(n-1) a1, putting the value of an: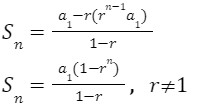
Using the formula for sum of geometric sequence- 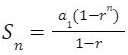
s20 = 5(1-220)/(1-2)
S20 = 5242875
Infinite Geometric series:
A geometric series with r<1 and with infinite number of terms is called an infinite geometric series.
Ex. 1/2 , 1/4 , 1/8 , …..
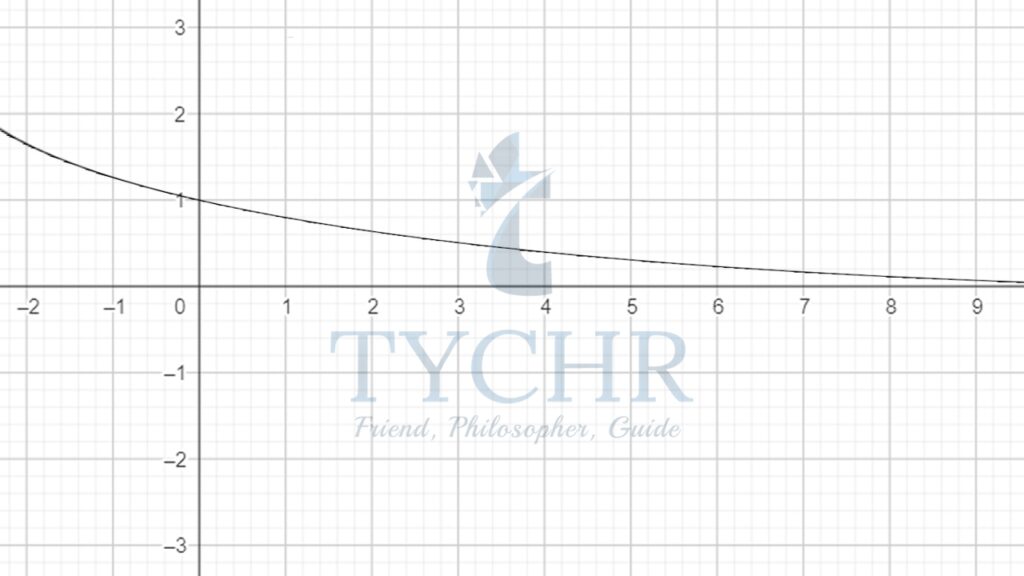
Consider the graph of y=rn when r<1 and n>0:
Observe the graph carefully, as n tends to infinity, rn tends to zero!
Keeping this in mind, let’s calculate the sum of infinite geometric sequence:
We know that the sum of geometric sequence is 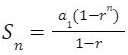
Ex. Find the sum:
20+10+5+….
The given series is an infinite geometric series, so we will use the formula- S = a1/(1-r)
a1=20 , r = 1/2
S = 20 / (1-(1/2))
S=40
APPLICATIONS OF ARITHMETIC AND GEOMETRIC PATTERNS
COMPOUND INTEREST
Assume, amount P is invested that yields an annual interest rate r. The interest is added to the amount at the end of the year. We can calculate the amount A at the end of t years by the use of geometric sequence formula. Consider the following table:
Time in years | Amount in the account |
| 0 | A0 = P |
| 1 | A1 = P + Pr = P(1 + r) |
| 2 | A2 = A1 + A1r = A1 (1+r) = P(1+r)2 |
| ⋮ | ⋮ |
| t | At = P(1+r)t |
So, we get the formula for amount after t years of compond interest at rate r as- At = P(1+r)t
Similarly, if the interest is compounded n times per year then r/n is the interest rate. And since every year we’ll have n periods, then for t years we have nt periods, which makes the formula- A = P(1+(r/n))nt
Ex. Oliver’s savings account now has a balance of $900. If the interest rate was 1.5% per annum compounded quarterly, how much did Oliver originally deposit six years ago if he has not withdrawn or deposited any money since?
Using the second formula:
A = P(1+(r/n))nt
We are given A=$900, r=1.5%, n=4(quarterly), t=6:
POPULATION GROWTH
The same formulae (the ones we deduced for compound interest) can be applied when dealing with population growth.
Ex. The population of Baden in Austria grows at an annual rate of 0.35%. The population of Baden in 1981 was 23140. What is the estimate of the population of Baden for 2025?
Now, we can consider a geometric sequence for this situation.
Let the first term be the population in 1981 i.e. a1=23140 and let the common ratio with the multiplying factor for each year i.e. r = (1 + (0.35/100)) = 1.0035
Now, in 2025, it will be 45 years since 1981, so we take number of terms to be 45.
Now we apply the formula of n^(th )term of geometric sequence:
an = a1(r)n-1
a45 = 23140(1.0035)44
a45 = 26985
Therefore, the population in 2025 will be 26,985.
THE BINOMIAL THEOREM
PERMUTATION
Permutation relates to the act of arranging all the members of a set into some sequence or order, or if the set is already ordered, rearranging its elements, a process called permuting. They often arise when different orderings on certain finite sets are considered.
A permutation is the choice of r things from a set of n things without replacement and where the order matters.
rn𝑷 = 𝒏!/(𝒏−𝒓)!, n>r
Ex. 15 students take part in a race. In how many ways can the top 3 positions be filled?
Since the students are all different, this is a permutation of 15 objects taken 3 at a time.
315𝑃 = 15!/(15−3)! = 2730
COMBINATION
The combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter. In smaller cases, it is possible to count the number of combinations. Combination refers to the combination of n things taken r at a time without repetition.
Ex. In how many ways a committee consisting of 5 men and 3 women, can be chosen from 9 men and 12 women.
Choose 5 men out of 9 men = 59C ways = 9!/4!5! = 126 ways
Choose 3 women out of 12 women = 312C ways = 12!/3!9! =220 ways
The committee can be chosen in 59C×312C=126×220=27720
Note: Pascal’s Rule:
- rnC=n+rnC
- r-1 n C+ rnC=rn + 1C
BINOMIAL THEOREM
A binomial is a polynomial with two terms. For example, x+y is a binomial.
The binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial.
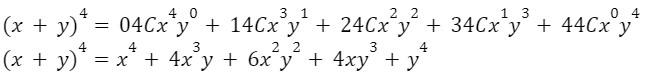
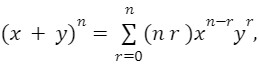
We have n=9
which makes r=6
So the required term is 69C(2a)3(-3b)6 = 489888a3b6
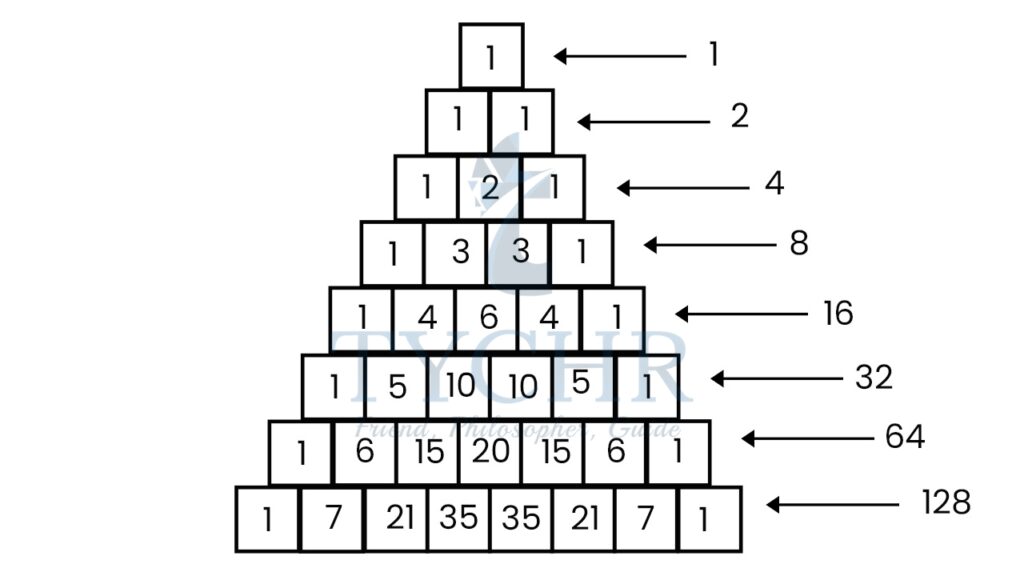
PASCAL’S TRIAN GLE
Pascal’s triangle is a triangular array constructed by summing adjacent elements in preceding rows. Pascal’s triangle contains the values of the binomial coefficient.
The first row gives the coefficients of terms of (x+y)1
The second row gives the coefficients of terms of (x+y)2
The third row gives the coefficients of terms of (x+y)3
And so on.