sequences and series Notes
SEQUENCES AND SERIES
By the end of this chapter you should be familiar with:
- nth term for Arithmetic and Geometric sequences
- Sum of n terms for Arithmetic and Geometric series
- Using Sigma Notation
- Applications
- Annuities and Amortization
A sequence is an arrangement of any objects or a set of numbers in a particular order followed by some rule. If a1, a2, a3, a4,……… etc., denote the terms of a sequence, then 1,2,3,4,…..denotes the position of the term.
A sequence can be defined based upon the number of terms i.e. either finite sequence or infinite sequence.
If a1, a2, a3, a4, ……. is a sequence, then the corresponding series is given by
SN = a1+a2+a3 + .. + an
Series a number of events, objects, or people of a similar or related kind coming one after another.
Note: The series is finite or infinite depending if the sequence is finite or infinite.
SEQUENCE | SERIES |
Set of elements that follow a pattern | Sum of elements of the sequence |
Order of elements is important | Order of elements is not so important |
Finite sequence: 1,2,3,4,5 | Finite series: 1+2+3+4+5 |
Infinite sequence: 1,2,3,4,…… | Infinite Series: 1+2+3+4+…… |
TYPES OF SEQUENCE AND SERIES
- Arithmetic
- Geometric
- Harmonic
- Fibonacci Numbers
Where we’ll be studying arithmetic and geometric in detail.
Harmonic Sequences
A series of numbers is said to be in harmonic sequence if the reciprocals of all the elements of the sequence form an arithmetic sequence.
Fibonacci Numbers
Fibonacci numbers form an interesting sequence of numbers in which each element is obtained by adding two preceding elements and the sequence starts with 0 and 1. Sequence is defined as, F0 = 0 and F1 = 1 and Fn = Fn-1 + Fn-2
ARITHMETIC SEQUENCES
A sequence a1, a2, a3, …., an is an arithmetic sequence if there is a constant d for which
an = an-1 + d
for all integers n > 1, d is called the common difference of the sequence, and d = an – an-1 for all integers n > 1.
The general (nth) term of an arithmetic sequence, an, with first term a1 and common difference d, may be expressed explicitly as:
an = a1 + (n – 1)d
Example 1: f a sequence has a first term of a1 = 12 and a common difference d = −7. Write the formula that describes this sequence. Use the formula of the arithmetic sequence.
Solution: As we know, an = a1 + (n-1)d
an = 12 + (n-1)(-7) = 12 – 7n + 7
an = -7n+19
Example 2: Write down the first five terms of the arithmetic progression with first term 8 and common difference 7.
Solution: We have a=8 and d=7.
The form of an arithmetic progression is a, a+d, a+2d, a+3d, a+4d so using these values of a and d the first five terms are:
= 8, 8+7, 8+(2×7), 8+(3×7), 8+(4×7)
= 8, 15, 22, 29, 36
Simple Interest
Suppose you deposit an amount of a into a bank. We refer to a as the principal balance. You are paid 15% interest on your deposit at the end of each year (per annum). At the end of the first year you will have a total of:
(a + 0.15×a) = a(1+0.15) = 1.15a
With simple interest, the key assumption is that you withdraw the interest from the bank as soon as it is paid and deposit it into a separate bank account. This means that the interest paid each year is only ever paid on the principal balance. At the end of the second year you will therefore have a total of:
(a+0.15a+0.15a) = (a(1+2×0.15))
At the end of the third year you will have:
(a+ 0.15a +0.15a+ 0.15a) = (a(1+3×0.15))
and so on till n years i.e., (a(1+n×0.15))
We can see that the total balance-the principal balance and the interest earned each year up to the present year-forms an arithmetic progression with first term a and common difference 0.15a.
In general, for an interest rate of r per annum and principal balance of A, the total balance will form an arithmetic progression with first term A and common difference d=r × a. Using the above formula for the nth term of an arithmetic progression, the total balance at the end of n years is a + nd.
Example: James deposits £2,000 into a bank which pays an annual interest rate of 4%. He withdraws and spends the interest earned every time it is paid. Calculate:
- James’ total balance after 55 years
- The interest that he receives after 55 years
Solution: a) As James withdraws the interest earned each year, his total balance forms an arithmetic sequence with first term a=2,000 and common difference d = 0.04×2000 = 80. We want to calculate his total balance after 5 years. Using the formula with n=5 we have:
Total balance = £ (2,000 + (5×80)) = £ 2,400
b) The interest that James receives over 5years is equal to the difference between his total balance after 5years and his principal sum. We know that James’ principal sum is £2,000 and we found in part a) that his total balance after 5 years is £2,400. The interest received over 5 years is thus:
£ 2,400 − £ 2,000 = £ 400
GEOMETRIC SEQUENCES
A sequence a1, a2, a3, …, an is a geometric sequence if there is a constant r for which
an = an-1 x r for all integers n > 1
r is called the common ratio of the sequence, and r = an ÷ an-1 for all integers n > 1. The general (nth) term of a geometric sequence, an, with common ratio r and first term a1, may be expressed explicitly as
an = a1 x rn-1
Example 1: Write down the first five terms of the geometric progression which has first term 1 and common ratio 12.
Solution: We have a = 1 and r = 1/2. The general form of a geometric progression is a, ar, ar2, ar3, ar4,… so using these values of a and r the first five terms are:
1, 1×(1/2), 1×(1/2)2, 1×(1/2)3, 1×(1/2)4
1, 1/2 , 1/4, 1/8, 1/16
As we can see, the terms are getting smaller and smaller.
Example 2: Find the 10th term of the geometric progression with first term 3 and common ratio 2.
Solution: We have a=3, r=2 and n=10. Using the formula for the nth term, the 10th term is
3 × 210-1 = 3 × 29 = 1536
Compound Interest
The difference between simple interest and compound interest is that with compound interest it is assumed that you do not withdraw the interest earned from the bank each time it is paid. At the end of each year, the interest will therefore be paid on the total balance earned so far (the principal sum and interest earned each year up to the present year).
If the principal sum is a and the interest rate is r per annum the total balance at the end of the first year will be: a(1+r)
At the end of the second year it will be: a(1+r)2
At the end of the third year it will be: a(1+r)3
and so on.
We can see that the total balance forms a geometric progression with first term a and common ratio (1+r). Using the above formula for the nth term of a geometric progression with n−1 replaced by n, the total balance at the end of n years is: a(1+r)n
Note: The total balance at the beginning of the nth year is given by: a(1+r)n-1
Now suppose that the bank pays you interest on your deposit t times per year. For example, interest might be paid monthly, in which case we would have t=12. Assuming that the interest earned is not withdrawn after each payment, the total balance after n years is given by: a(1 +(r/t) ) tn
where, as before, r is the interest rate and A is the principal sum.
Example: After discovering that his wife is in fact having triplets, James takes up a part time job to pay for their combined clothing costs and decides that he will enough money into a bank account to pay for a car worth 3,000 for each of them on their 18th birthday. Assuming that the interest rate is 25% and that James does not withdraw the interest payment each year, how much does James now need to deposit into the bank account?
Solution: As James leaves the interested earned each year in the account, his total balance forms a geometric sequence with first term a and common ratio 1+0.25 = 1.04. Since each car costs £3,000, the combined cost is 3×3000=9000. This is the total balance that James must have after 18 years. Using the formula with n=18, we have:
9,000 = a(1.2518) = 55.511a
Rearranging and solving this equation for a gives:
a = 162.129
So, James needs to deposit £162.129 in order to have a total balance of at least £9,000 by his children’s 18th birthday.
SIGMA NOTATION
The Summation Operator ∑ is used to denote the sum of a sequence. We call the sum of the terms in a sequence a series. The starting index is written underneath and the final index above, and the sequence to be summed is written on the right. A series does not have to be the sum of all the terms in a sequence.
Rules:
Constant Rule 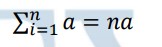
Constant Multiple Rule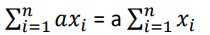
The Sum of Sequences Rule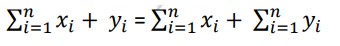
ARITHMETIC SERIES
Arithmetic series is the sum of the terms of an Arithmetic sequence a1, a2, a3, …, an. The sum, Sn, of n terms of an arithmetic series with common difference d, first term a1, and nth term an is
Sn = (n( a1 + an)) / 2 or Sn = (n(2a1 + (n – 1)d) / 2
Arithmetic mean is given by: an-1 = (an + an-2)/2
This means in the sequence above a2, a3, a4, …., an-1 are arithmetic mean between a1 and an
Example: Find the sum of the first 40 terms of the arithmetic series 2+5+8+11+…
Solution: First find the 40th term:
a40 = a1 + (n−1)d = 2 + 39(3) =119
Then find the sum: Sn = n (a1 + an)/2 S10 = 40(2 + 119)/2 = 2420
GEOMETRIC SERIES
Geometric series is the sum of the terms of a geometric sequence a1, a2, a3, …, an
The sum, Sn, of a finite geometric series with first term a, and common ratio r is given by:
Sn = a((1-rn)/(1-r))
The sum, S, of an infinite geometric series with first term a, such that the common ratio r satisfies the condition |r| < 1 is given by:
S =a/(1-r)
Geometric mean is the central number in a geometric progression given by:
a2 = √(𝒂𝟏 × 𝒂𝟑)
Example 1: Find the sum of the series S7 = 1−1/√2 + 1/2 – 1/2√2 + 1/4 – 1/4√2+ 1/8
Solution: This is a geometric progression with r =−1/√2. Since the sum of a geometric progression is given by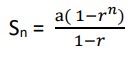
we have,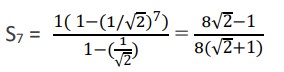
Example 2: Solve the equation x2 − 2x3 + 4x4 − 8x5 +… = 2x+1, |x|<1
Solution: We know that, S =a/(a-r)
x2 − 2x3 + 4x4 − 8x5 +… = x2(1 − 2x + 4x2 − 8x3 +…) =x2/(1-(-2x))= x2/(1+2x)
Then, x2/(1+2x)= 2x + 1
3x2 + 4x + 1 = 0 = -1 or -1/3 As |x|<1, x = -1/3

ANNUITIES AND AMORTIZATION
Annuities are a sequence of equal payments made at regular time intervals and amortization determines sequence of payments.
Present Value of Annuity:
Amortization: 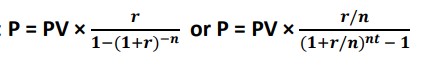
Example 1: Jolene deposits $100 every month into an annuity at 5% compounded monthly, for 9 years. Find the future value and the interest her account earned.
Solution: By using the formula 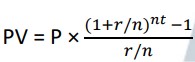
Jolene’s future value will be 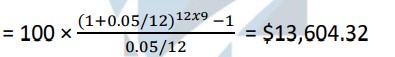
Example 2: Dave wants to save $20,000 for a down payment on a really cool speedboat. He opens an annuity at 4.25% compounded quarterly for 3 years. What is his quarterly payment?
Solution: By using the formula 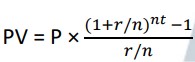
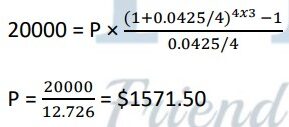
$1571.50 is the quarterly deposit.

