energetics and thermochemistry Notes
Measuring energy changes
Energy and heat transfer energy
- Thermodynamics is the study of energy and how it is interconverted.
- The first law of thermodynamics states that energy can be converted from one form to another and that the total amount of energy for a given system will remain constant.
- This law is often called the law of conservation of energy and states that energy can be neither created nor destroyed; it can only be converted between different forms.
System and surroundings
- Most chemical reactions take place in an open system which can exchange energy and matter with the surroundings.
A closed system can exchange energy but not matter with the surroundings. - Although energy can be exchanged between a system and the surroundings, the total energy cannot change during the process; any energy lost by the system is gained by the surroundings and vice versa.
The heat content of a system is its enthalpy
- Enthalpy (H) is a measure of the amount of heat energy contained in a substance. It is stored in the chemical bonds and intermolecular forces as potential energy.
- When substances react, the difference in the enthalpy between the reactants and products (at constant pressure) results in a heat change which can be observed.
- The term “enthalpy,” derived from the Greek word for “heat inside,” refers to the system’s heat content. A system functions like a heat reservoir.
- When heat is added to a system from the surroundings its enthalpy increases.
- Changes in enthalpy are denoted by ∆H. ∆H is positive when heat is added to the system.
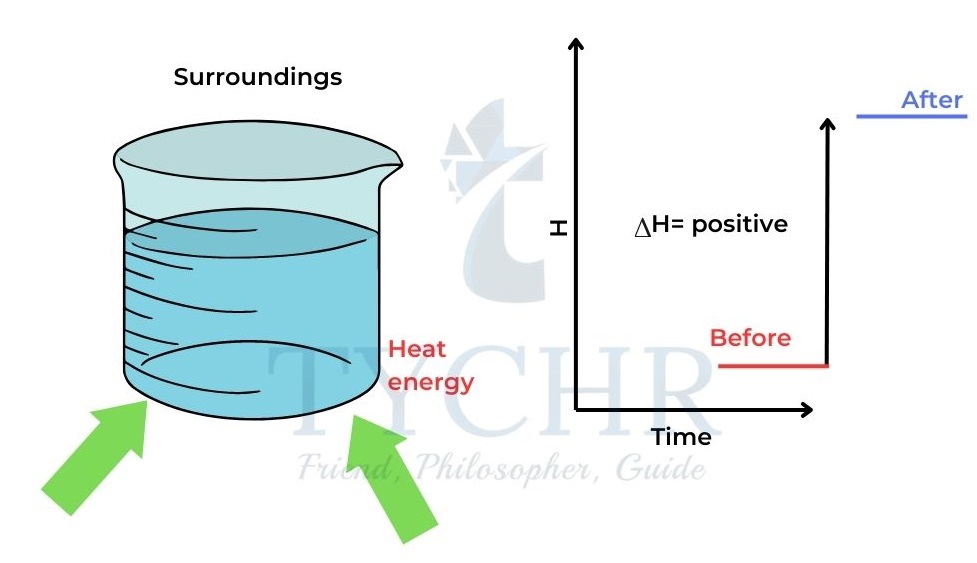
Figure 1: When heat is gained by the system from the surroundings, the enthalpy of the system increases and
∆H is positive. - When heat is released from the system to the surroundings the enthalpy of the system
decreases and ∆H is negative.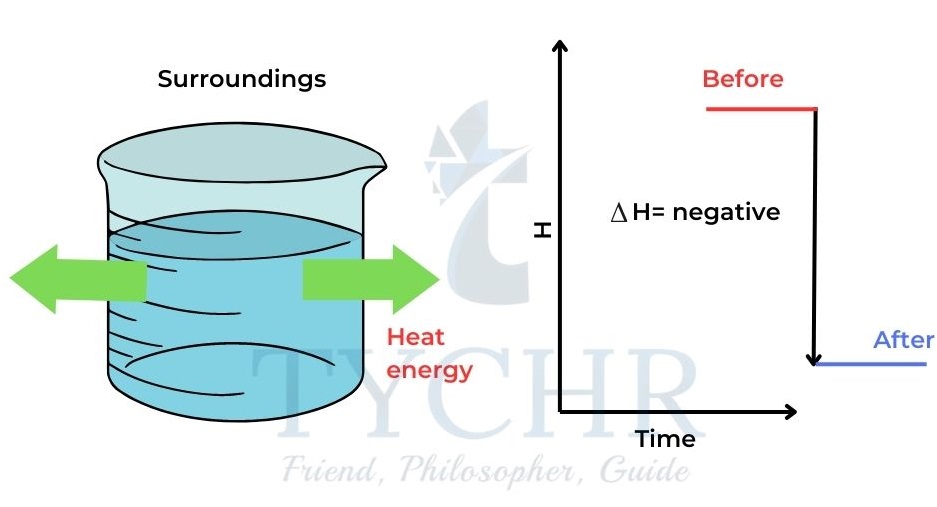
Figure 2: When heat is lost from the system to the surroundings the enthalpy of the system decreases and ∆H is negative.
Exothermic and endothermic reactions
- When substances react, the difference in the enthalpy between the reactants and products produces an enthalpy change which can be observed.
- Most chemical reactions, including most combustion and all neutralization reactions, are exothermic.
- They give out heat and result in a transfer of enthalpy from the chemicals to the surroundings and ∆Hreaction is negative.
- A few reactions are endothermic as they result in an energy transfer from the surroundings to the system.
In this case the products have more enthalpy than the reactants and ∆H is positive. - For exothermic reactions heat is given out by the system and ∆H is negative.
- For endothermic reactions heat is absorbed by the system and ∆H is positive.
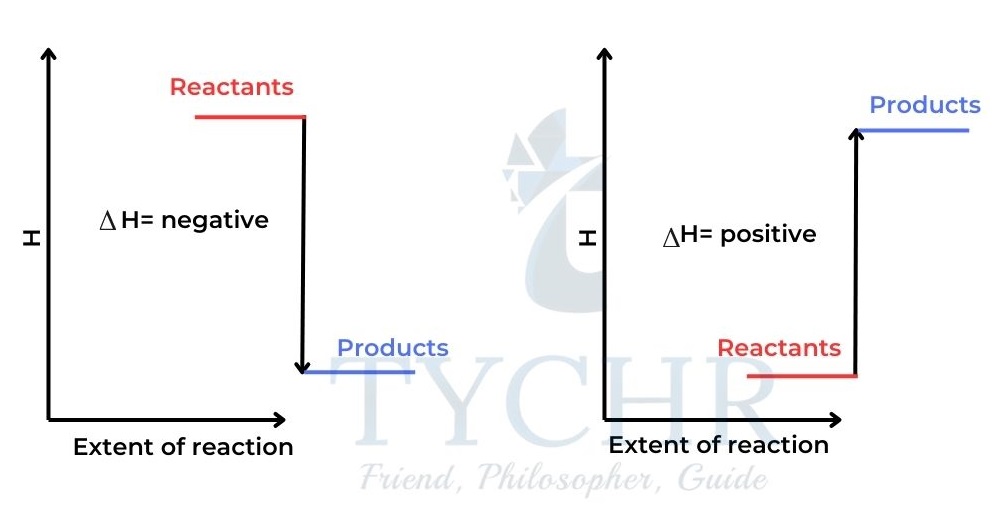
Figure 3: (a) An exothermic reaction. The products’ enthalpy is lower than that of the reactants.
(b) An endothermic reaction. The enthalpy of the products is greater than the enthalpy of the reactants.
Standard enthalpy changes
- As the enthalpy of a system also depends on the intermolecular forces of the reactants and products, the enthalpy change for a reaction depends on the conditions under which the reaction occurs.
- The standard enthalpy changes, ∆H⊖, given in the literature are measured under the following conditions:
- a pressure of 100 kPa
- concentration of 1 mol dm–3 for all solutions
- all substances in their standard states.
Heat changes can be calculated from temperature changes
- If the same amount of heat is added to two different objects, the temperature change will not be the same, as the average kinetic energy of the particles will not increase by the same amount.
- The object with the smaller number of particles will experience the larger temperature increase, as the same energy is shared amongst a smaller collection of particles.
- In general, the increase in temperature when an object is heated depends on:
- The mass of the object
- The heat added
- The nature of the substance.
- The number of particles in a unit mass sample, which in turn will depend on the mass of the individual particles, determines the specific heat capacity.
heat change (q) = mass (m) × specific heat capacity (c) × temperature change (∆T)
- When considering the relationship between different objects the heat capacity is often a more convenient property. The heat capacity (C) is defined as the heat needed to increase the temperature of an object by 1 K.
Heat capacity (C) =𝐡𝐞𝐚𝐭 𝐜𝐡𝐚𝐧𝐠𝐞(𝐪)/ 𝐭𝐞𝐦𝐩𝐞𝐫𝐚𝐭𝐮𝐫𝐞 𝐜𝐡𝐚𝐧𝐠𝐞(∆𝐓 )
Enthalpy changes and the direction of change
- There is a natural direction for change.
- Methane burns when we strike a match and form carbon dioxide and water. The chemicals are changing in a way which reduces their enthalpy.
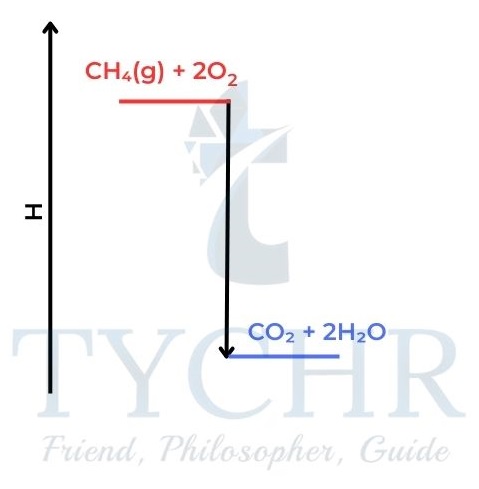
Figure 4: An exothermic reaction can be compared to a person falling off a ladder. Both changes lead to a decrease in stored energy. The state of lower energy is more stable. The mixture of carbon dioxide and water is more stable than a mixture of methane and oxygen. - Measuring enthalpy changes of combustion:
The standard enthalpy change of combustion (∆H⊖c) is the enthalpy change for the complete combustion of one mole of a substance in its standard state in excess oxygen under standard conditions.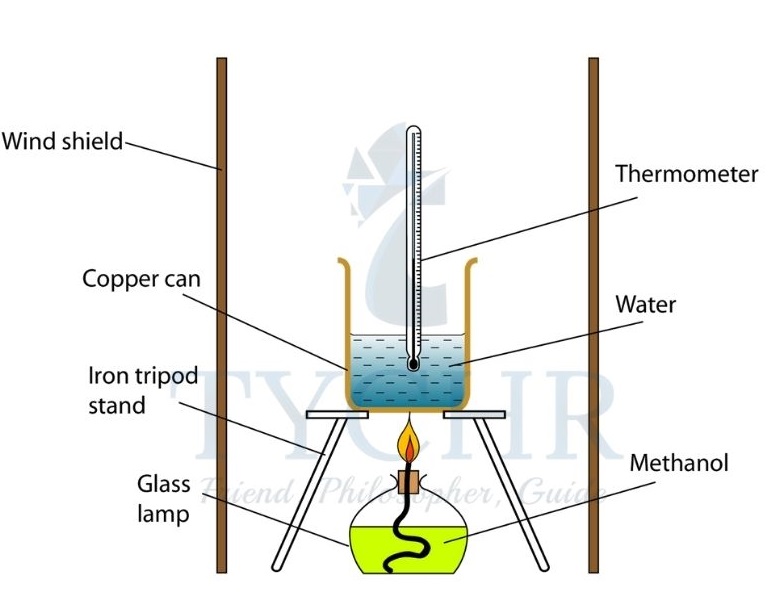
Figure 5 The temperature change of the water in the metal calorimeter is used to calculate the heat produced by fuel combustion. Copper is a good heat conductor, so the water can absorb heat from the flame.: - The temperature of the water increases as it has increased its heat content, owing to the heat released by the combustion reaction.
- There is a decrease of enthalpy during the reaction.
Calculating enthalpies of reaction from temperature changes
- When the heat released by an exothermic reaction is absorbed by water, the temperature of the water increases. The heat produced by the reaction can be calculated if it is assumed that all the heat is absorbed by the water.
∆Hreaction = –∆H(water) = –m(H2O) × c(H2O) × ∆T(H2O) - As the water has gained the heat produced by the reaction, the enthalpy change of reaction is negative when the temperature of the water increases.
Enthalpy changes of reaction in solution
- The enthalpy changes of reaction in solution can be calculated by carrying out the reaction in an insulated system, for example, a polystyrene cup (Figure 6).
- The heat released or absorbed by the reaction can be measured from the temperature change of the water.
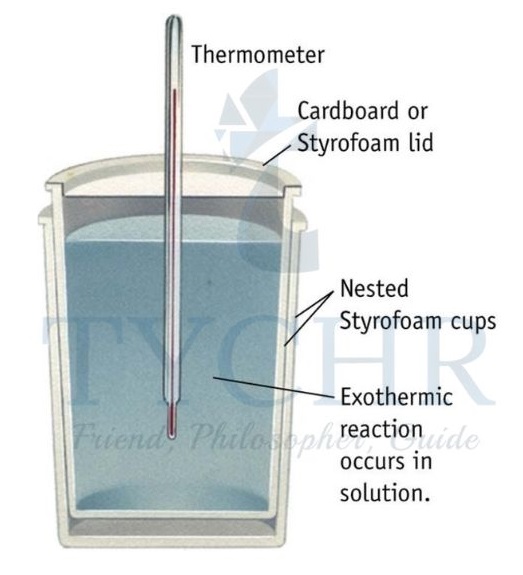
Figure 6: A simple calorimeter. The polystyrene is a very good thermal insulator with a low heat capacity.
Enthalpy cycles
- The enthalpy change for a particular reaction is calculated from the known enthalpy change of other reactions. Consider the energy cycle in Figure 7.
- Carbon and hydrogen are first combined to make ethanol in the clockwise direction, and then ethanol is burned. The elements are burned one at a time in the anticlockwise direction.
- The experimentally determined enthalpy changes are included in the figure.
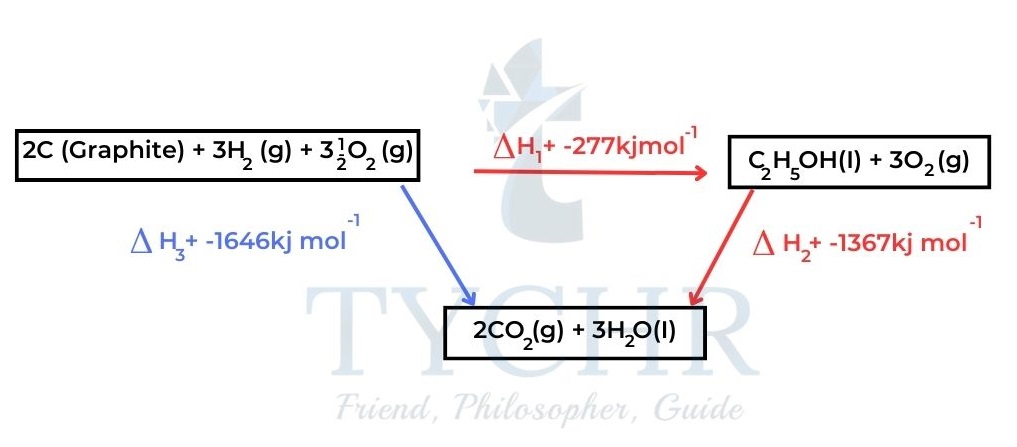
Figure 7: In the clockwise route, the elements are first combined to form ethanol and then ethanol is burned.
In the anticlockwise route, the elements are burned separately. - Consider the clockwise route: ∆H1 + ∆H2 = –277 + –1367 = –1644 kJ mol–1
- Consider the anticlockwise route: ∆H3 = –1646 kJ mol–1
- Given the uncertainty of the experimental values, we can conclude that: ∆H3 = ∆H1 + ∆H2
- Consider a clockwise cycle in which carbon and hydrogen and oxygen are converted to ethanol and then carbon dioxide and water, which are then converted to the original elements.
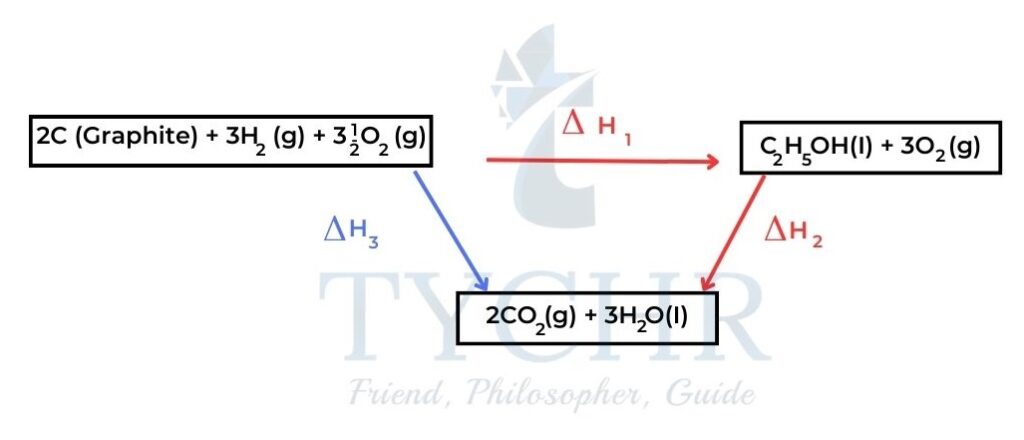
Figure 8: There is no net chemical change in a complete cycle as the starting reactants and final products are the same. - Hess’s law states that the enthalpy change for any chemical reaction is independent of the route, provided the starting conditions and final conditions, and reactants and products, are the same.
Standard enthalpy changes of reaction
- The enthalpy change of a reaction depends on the physical state of the reactants and the products and the conditions under which the reaction occurs.
- For this reason, standard enthalpy changes, ∆H⊖, which are measured under standard conditions of 298 K (25 °C) and 1.00 × 105 Pa, are generally tabulated.
- The standard enthalpy change of formation, ∆H⊖f, of a substance is the enthalpy change that occurs when one mole of the substance is formed from its elements in their standard states.
- These standard measurements are taken at a temperature of 298 K (25 °C) and a pressure of
1.00 × 105 Pa. They are important as they: - give a measure of the stability of a substance relative to its elements
- It can be used to calculate the enthalpy changes of all reactions, either hypothetical or real.
Using standard enthalpy changes of formation
- Standard enthalpy changes of formation can be used to calculate the standard enthalpy change of any reaction. Consider the general energy cycle in Figure 9.
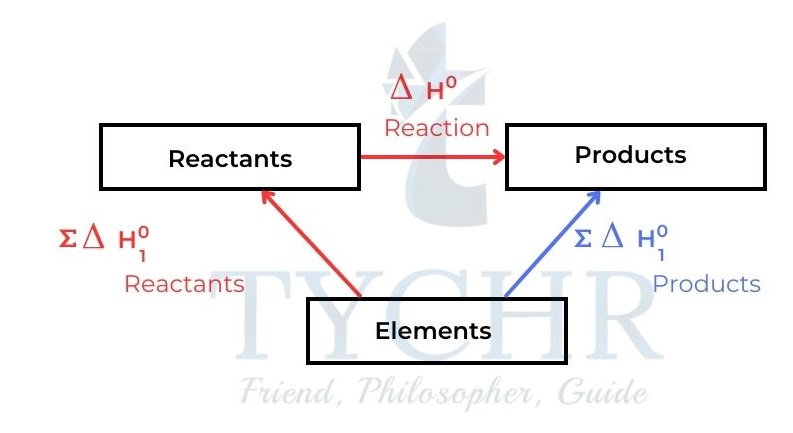
Figure 9: The chemical change elements → products can either occur directly or indirectly. The total enthalpy change must be the same for both routes. ∑ means ‘the sum of - We have from the diagram:
∑∆H⊖f (reactants) + ∆Hreaction = ∑∆H⊖f (products) - This gives the general expression for ∆Hreaction of any reaction
∆Hreaction= ∑∆H⊖f (products) – ∑∆H⊖f (reactants)
Bond enthalpies
Breaking bonds is an endothermic process
- A covalent bond is due to the electrostatic attraction between the shared pair of electrons and the positive nuclei of the bonded atoms.
- Energy is needed to separate the atoms in a bond. The bond enthalpy is the energy needed to break one mole of bonds in gaseous molecules under standard conditions.
- Using Hess’s law:
H2O(g) → H(g) + OH(g) ∆H = +502 kJ mol–1
OH(g) → H(g) + O(g) ∆H = +427 kJ mol–1 - Average bond enthalpy over numbers on right
H2O(g) → H(g) + H(g) + OH(g) ∆H = +502 + 427 kJ mol–1
Average bond enthalpy E(O–H) = (+502+ 427)/ 2 kJ mol–1 = 929/ 2 = 464.5 kJ mol–1
Making bonds is an exothermic process
- The same amount of energy is absorbed when a bond is broken as is given out when a bond is made (Figure 10). For example:
H(g) + H(g) → H2(g) ∆H⊖ = –436 kJ mol–1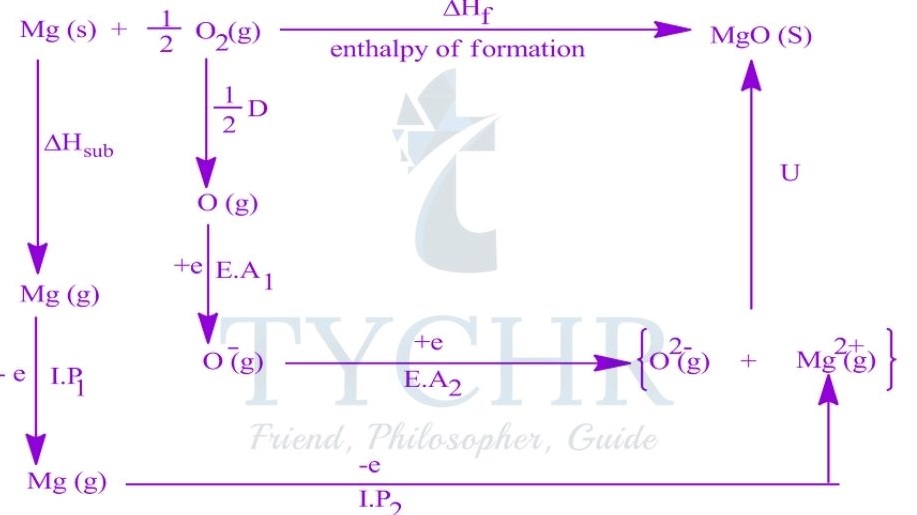
Figure 10: The energy changes that occur when bonds are broken and bonds are formed.
Ozone depletion
- The Earth is unique among the planets in having an atmosphere that is chemically active and rich in oxygen.
- Oxygen is present in two forms, normal oxygen (O2) and ozone (O3), and both forms play a key role in protecting life on the Earth’s surface from harmful ultraviolet (UV) radiation.
The natural formation and depletion of ozone
- In the stratosphere, the strong covalent double bond in normal oxygen O2 is broken by high- energy UV radiation with a wavelength shorter than 242 nm to form two oxygen atoms:
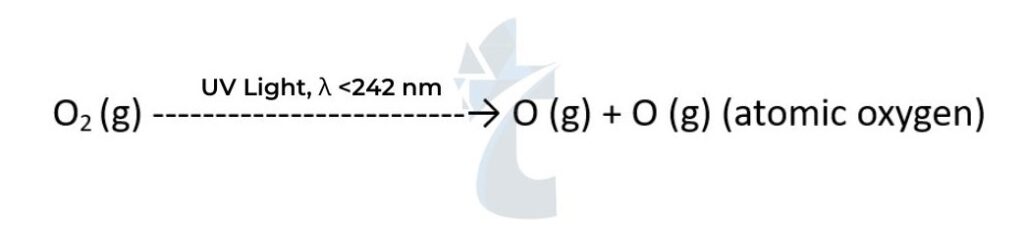
- The oxygen atoms have unpaired electrons. They are reactive free radicals and so react with another oxygen molecule to form ozone. O•(g) + O2(g) → O3(g) As the bonds in ozone are weaker than the double bond in oxygen, ultraviolet light of lower energy is needed to break them:

- The oxygen atoms then react with another ozone molecule to form two oxygen molecules.
O3(g) + O•(g) → 2O2(g) - As bonds are formed this is another exothermic reaction which produces heat that maintains the relatively high temperature of the stratosphere.
- The level of ozone in the stratosphere – less than 10 ppm – stays at a constant level if the rate of formation of ozone is balanced by its rate of removal. This is known as a steady state. The whole process is described by the Chapman Cycle.

- Because harmful ultraviolet light has been absorbed and the stratosphere has become warmer, this cycle of reactions is significant. Both of these processes are necessary for life on Earth to exist.
Energy cycles
First ionization energies and electron affinities
- The first ionization energy is the minimum energy required to remove one mole of electrons from one mole of gaseous atoms.
- The first electron affinity is the enthalpy change when one mole of gaseous electrons is added to one mole of gaseous atoms.
The Born–Haber cycle and enthalpy of formation
- The standard enthalpy of formation of an ionic compound can be represented by a single equation:
Na(s) + 1/ 2 Cl2(g) → NaCl(s) ΔHf = -411 kJ mol-1 - An application of Hess’s law. The Born–Haber cycle, is a series of reactions that can be combined to determine the enthalpy of formation of an ionic compound.
Constructing a Born–Haber cycle
- The Born–Haber cycle combines the enthalpy changes associated with several steps in the formation of an ionic compound, defined below.
Lattice enthalpy
- The lattice enthalpy is the enthalpy change that occurs when one mole of a solid ionic compound is separated into gaseous ions under standard conditions.
- The lattice enthalpy is defined as the standard enthalpy change that occurs on the formation of 1 mol of gaseous ions from the solid lattice:
MX(s) → M+(g) + X– (g) ∆Hlat> 0
Enthalpy of atomization
- The enthalpy of atomization ΔHat is the standard enthalpy change that occurs on the formation of 1 mol of separate gaseous atoms of an element in its standard state:
M(s) → M(g) ΔHat> 0
1/2 X2(g) → X(g) ΔHat> 0
Ionization energy
- The ionization energy, ΔHIE, is the standard enthalpy change that occurs on the removal of 1 mol of electrons from 1 mol of atoms or positively charged ions in the gaseous phase.
- For metal ions with multiple valence electrons the first, second, and sometimes third ionization energies are defined.
IE1: M(g) → M+(g) + e– ∆HIE1 > 0
IE2: M+(g) → M2+(g) + e– ∆HIE2 > 0
Electron affinity
- The electron affinity, ∆HEA, is the standard enthalpy change on the addition of 1 mol of
electrons to 1 mol of atoms in the gaseous phase:
X(g) + e– → X– (g) ∆HEA < 0
Constructing the Born–Haber cycle
- The lattice enthalpy, the enthalpy of atomization, the ionization energy, and the electron affinity are combined to construct the Born–Haber cycle and find the enthalpy of formation of an ionic compound.
- The standard Born–Haber cycle focuses on the processes involved and the relationships between the individual steps rather than the magnitude of each energy change.
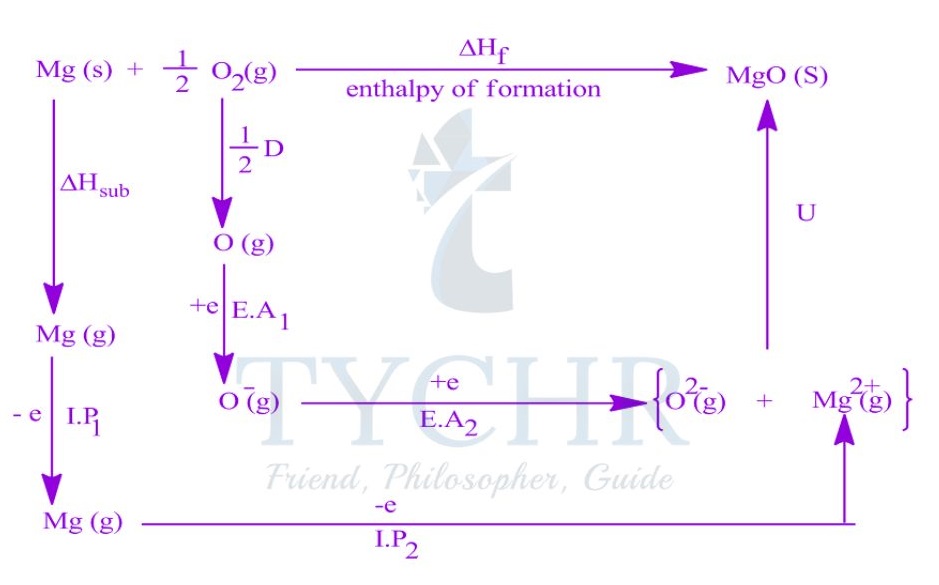
Variations in lattice enthalpy values
- The ionic radii and charge on the ions have a direct impact on the magnitude of the lattice enthalpy for a compound.
- An increase in the ionic charge will result in a greater attraction between oppositely charged ions, increasing the energy required to break apart the ionic lattice, that is, the lattice enthalpy.
- For metal halides, the radius of the anion increases as you move down group 17 from fluorine to iodine. As the distance between the bonded ions increases, the strength of the electrostatic attraction decreases and this is reflected by a decrease in the lattice enthalpy.
Enthalpy changes in solution
- Many reactions studied in chemistry take place in solution. It is useful therefore to consider the enthalpy of solution and the relationship between the enthalpy change of solution, the hydration enthalpy, and the lattice enthalpy.
- The standard enthalpy change of solution, ∆Hsol, is the change in enthalpy when 1 mol of a substance is dissolved in a large excess of a pure solvent:
NH4Cl(s) → NH4+(aq) + Cl (aq) ∆Hsol = +14.78 kJ mol-1
LiBr(s) → Li+(aq) + Br (aq) ∆Hsol = -48.83 kJ mol-1
The enthalpy change of hydration, ∆Hhyd, for an ion is - the enthalpy change when 1 mol of the gaseous ion is added to water to form a dilute solution. The term solvation is used in place of hydration for solvents other than water.
M+(g) → M+(aq) ∆Hhyd= – kJ mol-1
X (g) → X (aq) ∆Hhyd= – kJ mol-1
Solvation, dissolution, and hydration
- Solvation is described as any stabilizing interaction of a solute and the solvent or a similar interaction of solvent with groups of an insoluble material.
- Electrostatic forces and van der Waals forces are common in these interactions, as well as chemically specific effects like the formation of hydrogen bonds.
- Water is a polar solvent. The difference in electronegativity between oxygen and hydrogen, combined with the geometry of the water molecule (bent) due to the repulsive forces between the lone pairs of electrons on the oxygen atom, result in this polar molecule having partial negative charges on the oxygen atom and partial positive charges on the hydrogen atoms.
- Water molecules orientate themselves so that their partial charges surround cations and anions, forming a solvation shell, also known as a hydration shell when the solvent is water.
- When solid sodium hydroxide is mixed with liquid water, a new homogeneous phase is formed known as the solution. This is the process of dissolution.
- The enthalpy of hydration is a way of quantifying the amount of energy released during the process of solvation. The magnitude of the enthalpy of hydration is influenced by the charge and size of the ion.
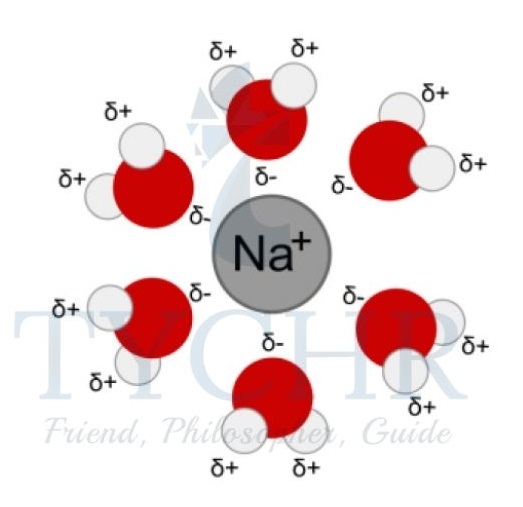
Figure 12: Solvation shell: the water (solvent) molecules surround a positively charged sodium ion.
Entropy and spontaneity
Spontaneous changes
- A reaction is said to be spontaneous when it moves towards either completion or equilibrium under a given set of conditions without external intervention.
- Reactions that are spontaneous can occur at different rates and may be either endothermic or exothermic.
- Non-spontaneous reactions are those that do not occur under a given set of circumstances.
Calculating entropy changes
- To calculate the standard entropy change associated with a reaction we find the difference between the total entropy of the products and the total entropy of the reactants:
∆S298(reaction) = ∑∆S298(products) – ∑∆S298(reactants) - When performing entropy change calculations the following points need to be considered:
- Remember that values for entropy are specific for different states of matter, for example, S (H2O(g)) = 188.8 J K-1mol-1 while S (H2O(l)) = 70.0 J K-1 mol-1
- When determining the overall entropy change, the equation’s coefficients must be applied to molar entropy values..
Gibbs free energy
- Along with entropy S, absolute temperature T, and enthalpy H, the Gibbs free energy G is a state function.
- The combination of enthalpy, entropy, and temperature of system can be used to define a new state function called Gibbs free energy, G:
G = H – TS
∆G = ∆H – T∆S - Focusing on a reaction system at constant temperature and pressure to determine its spontaneity can be done effectively using the Gibbs free energy.
- For a reaction to be spontaneous the Gibbs free energy must have a negative value (∆G < 0).
- Exothermic reactions that involve increasing disorder will always be spontaneous, with ∆G < 0.
- Similarly, endothermic reactions of increasing order will always be nonspontaneous, with ∆G
> 0. The spontaneity of other reactions depends on the temperature of the system.
Gibbs free energy change of formation
- When 1 mol of a compound is formed from its elements under standard conditions of 298 K and 100 kPa pressure, the Gibbs free energy change of formation, Gf, is represented.:
ΔGr = ΣΔGf (products) – ΣΔGf (reactants)
Calculation the gibbs free energy change of a reaction from enthalpy and entropy data
- To determine the spontaneity of a reaction from ∆G = ∆H – T∆S, we need to calculate the Gibbs free energy change for the reaction under standard conditions (298 K and 100 kPa).
- We must first calculate the changes in the reaction’s enthalpy and entropy if the Gibbs free energies of formation of the reactants and/or products are unknown. the

