Oscillations And Waves Theory Notes
Oscillations
Periodic motion:
A motion which repeats itself after equal intervals of time.
Examples are motion of a loaded spring, an object moving in a circle, a simple pendulum.
Terms related to periodic motion:
- Amplitude(A): maximum displacement from equilibrium position.
- Time period(T): the time taken for a complete oscillation.
- Frequency(f): the number of oscillations per unit time.
𝑓 =1/𝑇 - Angular frequency(ω): It is the equivalent of frequency.
𝜔 = 2𝜋𝑓 - Phase(φ): If the motion does not start from equilibrium position, then the motion leads or lags with respect to the motion starting from equilibrium position by φ.
- Generally, the amplitude of a natural oscillation decreases with time due to dissipative forces. Oscillations which maintain constant time period no matter the change in amplitude are called isochronous oscillations.
Simple harmonic motion:
It is a type of periodic motion in which the restoring force is proportional to negative of displacement from equilibrium position.
𝑎 𝛼 − 𝑥
- A spring loaded with a mass exhibits this motion.
𝐹 = −𝑘𝑥
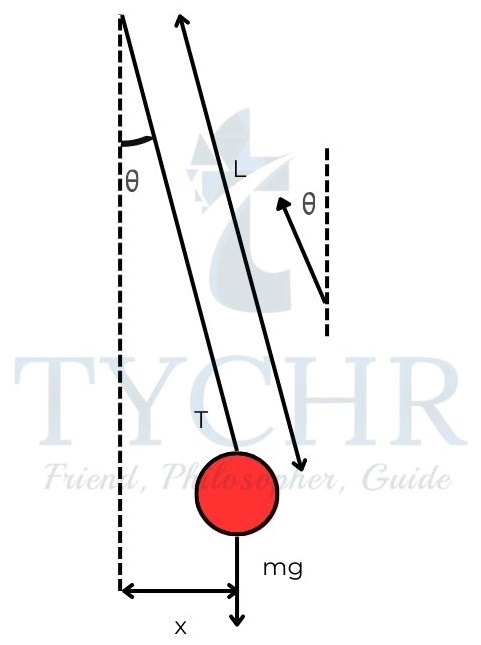
𝑎 = −(𝑘/𝑚)x - A simple pendulum with a small amplitude exhibits this behaviour.
The restoring force can be calculated to be −𝑚𝑔𝑠𝑖𝑛𝜃
For small amplitudes this can be approximated to (𝑚𝑔/𝐿)𝑥
𝑎 = −(𝑔/𝐿)𝑥
E.g.: The equation defining a simple harmonic motion is given by a = -kx.
a) What are the units of constant k?
b) Two systems S1 and S2 oscillate with constants k and 4k respectively. What is the difference in oscillations of two systems?
Answer.
a) 𝑘 = − 𝑎/x
So, the unit of k is 𝑚𝑠−2/𝑚 = 𝑠−2.
b) If the frequency of S1 is f, then S2 will have a frequency of √4f = 2f.
Describing simple harmonic motion:
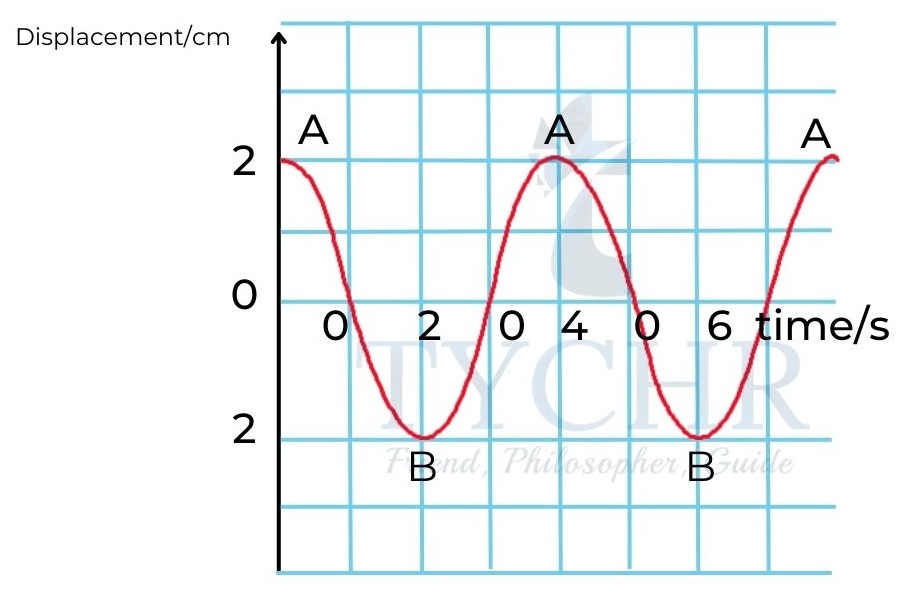
The motion of an object in simple harmonic motion can be described by the equation
𝑥 = 𝐴 sin(2𝜋𝑓𝑡 + 𝜑) = 𝐴𝑠𝑖𝑛(𝜔𝑡 + φ)
Here the phase φ is 𝜋/2. The oscillation starts at one of the extreme positions.
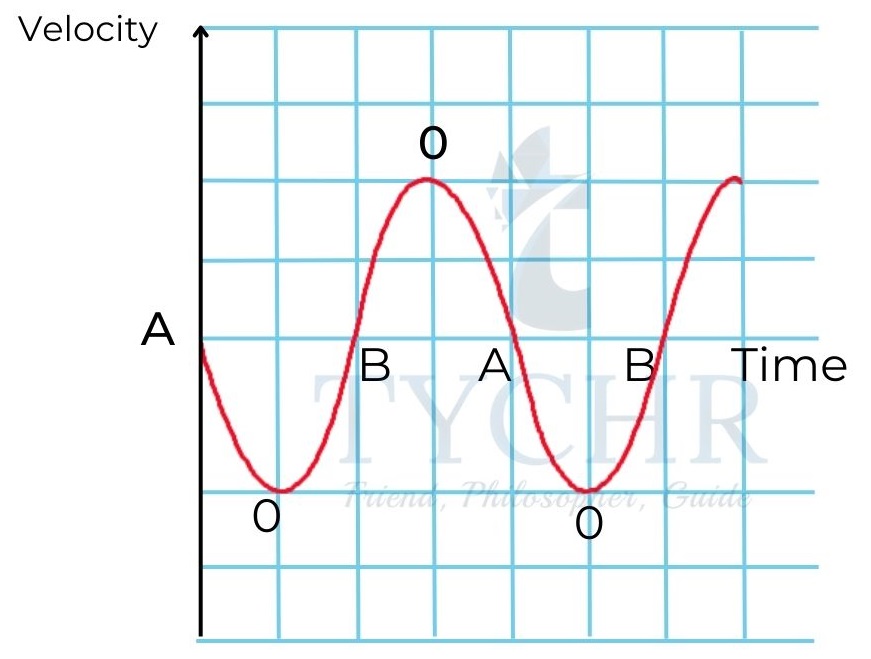
𝑣 =𝑑𝑥/𝑑𝑡 = 𝜔𝐴𝑐𝑜𝑠(𝜔𝑡 + φ) = 𝜔√𝐴2 − 𝑥2
The magnitude of velocity reaches maximum at equilibrium position and becomes zero at extreme positions.
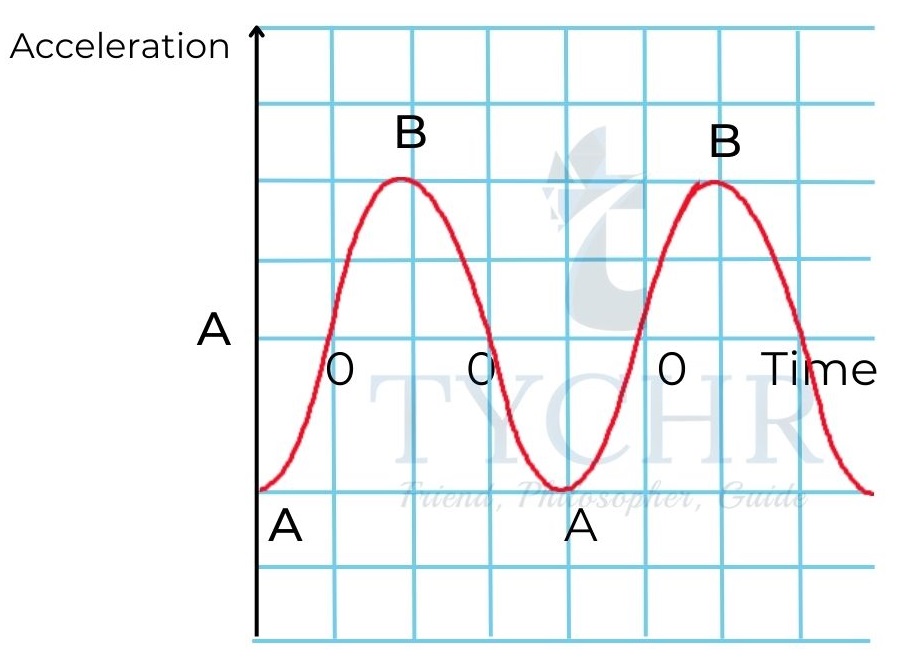
𝑎 =𝑑𝑣/𝑑𝑡 = −𝜔2𝐴𝑠𝑖𝑛(𝜔𝑡 + φ) = −𝜔2x
The magnitude of acceleration reaches maximum at extreme positions and becomes zero at equilibrium position.
E.g.: Calculate the phase difference between the two displacement-time graphs shown below in terms of a) seconds b) radi
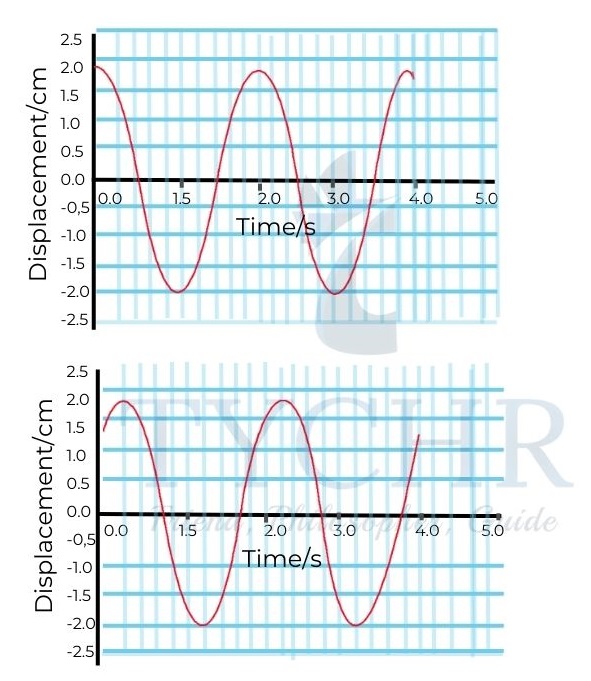
Answer.
Drawing vertical lines through the peaks of two curves gives the phase difference.
a) This appears to be ((0.25±0.01) s).
b) The time period is 2s. the phase difference in radians is 0.25 ×(2𝜋/2) = 0.79 radian

Circular motion and SHM:
The projection of an object executing circular motion on one of the diameters follows simple harmonic motion.
Consider an object moving in a circular motion of radius R with an angular velocity . Its projection on diameter executes simple harmonic motion whose displacement with respect to centre is given by 𝑥 = 𝑅𝑠𝑖𝑛(𝜔𝑡).
Energy changes in simple harmonic motion:
Kinetic energy: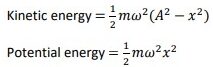
Total energy = (1/2)𝑚𝜔2𝐴2
The total energy of the object always remains constant in absence of dissipative forces.
Waves and its types
The particles of a wave vibrate about their mean position. The wave transfers energy from one place to another.
Waves are of two types:
- Mechanical waves: Which require a material medium to travel.
- Electromagnetic waves: Which can travel through vacuum.
Describing waves:
Wave front: A surface that travels with wave and is perpendicular to the direction in which wave travels.
Amplitude (A): The maximum displacement of wave from its equilibrium position.
Wavelength (λ): The shortest distance between two points in phase on a wave.
Period (T): The time taken for a complete wavelength to pass through a fixed point.
Frequency (f): Number of wavelengths passing through a fixed point per unit time.
𝑓 = 1/T
Travelling waves:
Travelling waves are of two types.
Transverse waves: The direction of vibration of waves is perpendicular to the direction of propagation of waves forming a series of crests and troughs.
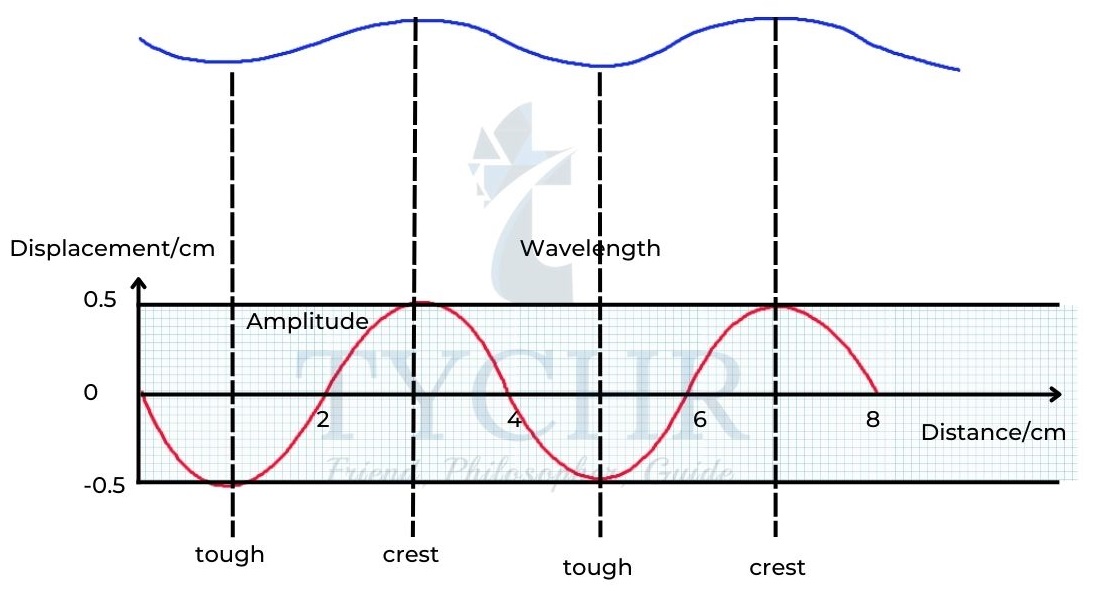
Longitudinal waves: The direction of vibration of waves is parallel to the direction of propagation of waves forming a series of compressions and rarefactions.
The wave equation:
The velocity of wave is given by c=fλ.
Where f is the frequency and λ is the wavelength of the wave.
E.g.: A wave travelling in an ocean has a wavelength 200m and time period 10s. find the wave velocity.
Answer. Frequency of the wave = = 1/10 = 0.1 Hz.
Wave velocity = 𝑓𝜆 = 0.1 × 200 = 20𝑚𝑠−1.
Electromagnetic waves:
Electromagnetic waves travel with varying electric and magnetic fields. They travel with a velocity of 3 × 108 ms-1 in vacuum and exhibit all properties of transverse waves.
Wave characteristics
Intensity of waves:
The intensity of waves (I) is the power received per unit area.
𝐼 =𝑝/4𝜋𝑟2
It is proportional to the square of amplitude.
𝐼 𝛼 𝐴2
E.g.: At a distance of 15m from the source, the intensity of a sound is 2 10-4Wm-2.
a) What is the intensity at a distance 120m from source.
b) How does the amplitude change?
Answer.
a) From the definition of intensity, intensity is inversely proportional to square of distance.
𝐼1/𝐼2 = 𝑟22/𝑟12
Which gives 𝐼2 = 3 × 10−6 Wm-2.
b)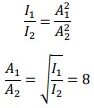
This implies A is inversely proportional to r.
The principle of superposition:
The principle of superposition says that, when two waves meet, the total displacement is the vector sum of their individual displacements.
Polarisation:
This phenomenon is only exhibited by transverse waves. Polarisation is a process in which the direction of oscillation is restricted to a plane perpendicular to the direction of propagation. A beam of light which has undergone polarisation is called plane-polarised light.
Polarisation of light can be achieved using a polaroid or when the light is incident on a surface at Brewster’s angle (the incident angle such that reflected and refracted rays are perpendicular).
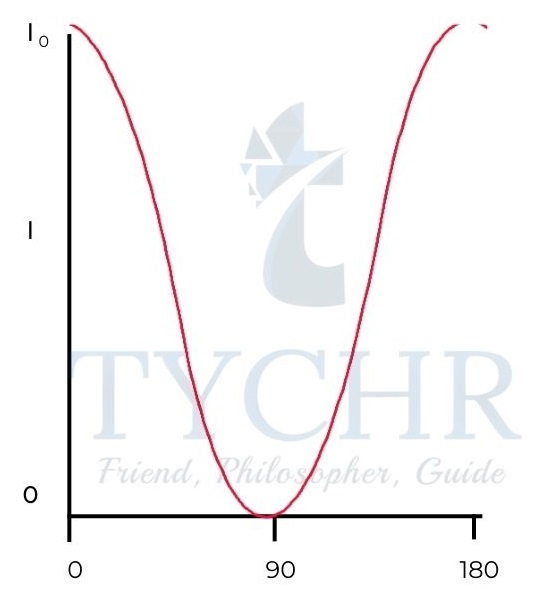
Malus’s law:
When a plane-polarized light from a polarizer is incident on an analyser (secondary polaroid), the intensity of light transmitted by the analyser is directly proportional to the square of cosine angle between polarizer and analyser.
𝐼 =𝐼0𝑐𝑜𝑠2𝜃
E.g.: A beam of plane-polarised light is incident on an analyser such that the angle between transmission axis and plane of polarisation is θ. Find the variation of the intensity of transmitted beam with θ.
Answer.
The intensity of transmitted beam varies as 𝐼 =𝐼0𝑐𝑜𝑠2𝜃
Wave behaviour
Reflection and refraction of waves:
Laws of reflection and refraction:
- The reflected, refracted, incident rays and the normal to the surface lie on the same plane.
- The angle of incidence equals angle of reflection.
- The ratio of angle of incidence and angle of refraction is constant for a particular frequency and a pair of media called refractive index.
Snell’s law:
For light going from medium 1 to medium 2,
𝑠𝑖𝑛𝜃1/𝑠𝑖𝑛𝜃2= 1𝑛2
Refractive index = 𝑠𝑝𝑒𝑒𝑑 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡 𝑖𝑛 𝑣𝑎𝑐𝑢𝑢𝑚/𝑠𝑝𝑒𝑒𝑑 𝑜𝑓 𝑙𝑖𝑔ℎ𝑡 𝑖𝑛 𝑚𝑒𝑑𝑖𝑢𝑚 = 𝑐/𝑣
Reversibility of light:
Light is reversible.
For light going from medium 1 to medium 2,
𝑠𝑖𝑛𝜃1/𝑠𝑖𝑛𝜃2= 1𝑛2
For light travelling in opposite direction,
𝑠𝑖𝑛𝜃1/𝑠𝑖𝑛𝜃2= 2𝑛1
E.g.: The refractive index of glass is 1.5 and that of water is 1.3.
a) Find the relative refractive index from glass to water.
b) Explain what this implies regarding refraction of light.
c) Draw a wave front diagram to show how light travels through a plane interface from glass to water.
Answer.
a) Relative refractive index from glass to water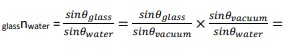
![]()
b) This means that the speed of light is faster in vacuum than water and bends away from normal.
c)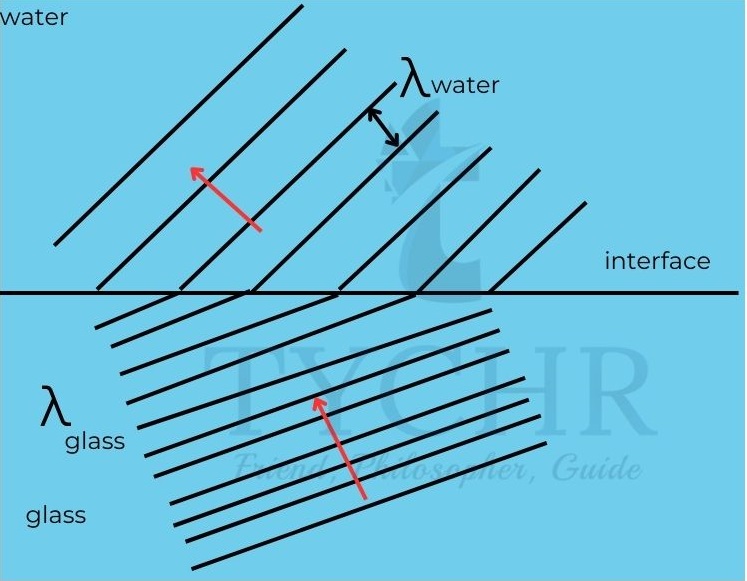
Critical angle and total internal reflection:
The angle of incidence for which the angle of refraction of a light ray travelling from an optically denser medium to rarer medium reaches right angle is called critical angle.
When the angle of incidence is greater than critical angle, the light gets completely reflected without being refracted. This phenomenon is called total internal reflection.
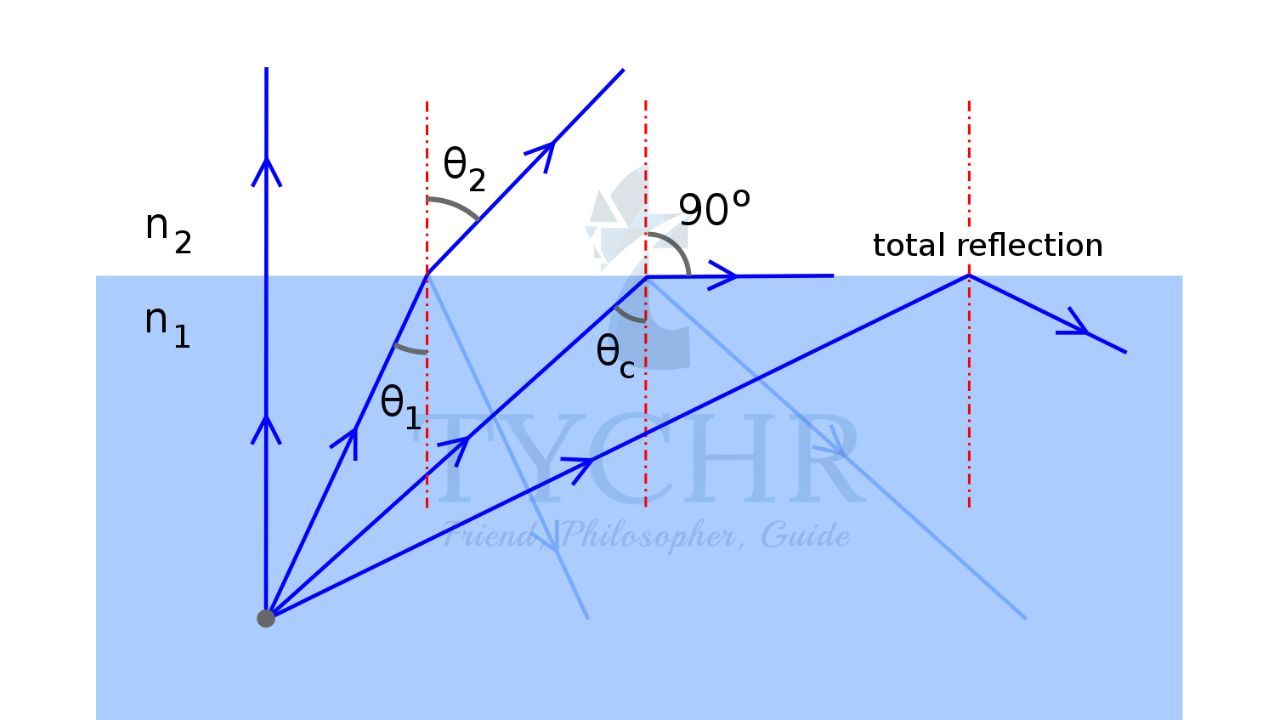
The critical angle is given by sin 𝜃𝑐 = 1/𝑛. Here n is the relative refractive index of denser material with respect to rarer material.
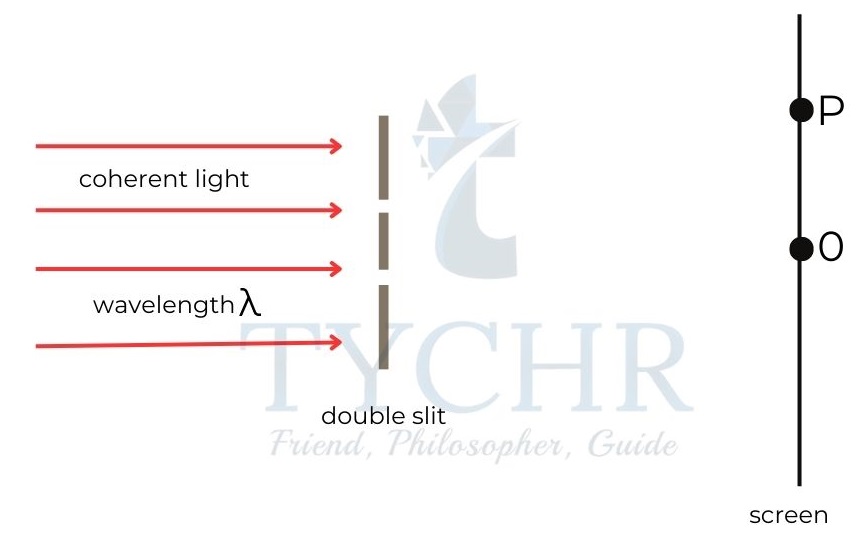
Double-slit interference:
It can be observed with two coherent (of same frequency) sources of any wave.
When two waves of the same frequency meet, they form a series of larger amplitudes and smaller amplitudes than the original wave. The regions of larger amplitude are due to constructive interference and that of smaller amplitude is due to destructive interference.
For constructive interference,
Path difference of two waves that meet should be equal to nλ, where n is a whole number. The amplitude of wave in such regions is the sum of amplitudes of two waves.
For destructive interference,
Path difference is (n +(1/2))λ, where n is a whole number. The amplitude of wave in such regions is the difference of amplitudes of two waves.
When the waves interfere on a screen placed parallel to the line of slits, the separation between two bands is 𝜆(𝐷/𝑑).

E.g.: In a double slit experiment of wavelength λ, the central bright fringe is observed at a point O. The path difference of waves arriving at P is 7 λ.
a.) Explain the nature of fringe at P.
b.) Explain the number of dark fringes between O and P.
Answer.
a) The path difference of waves arriving at P is an integer multiple of wavelength. So, a bright fringe is formed at P.
b) For destructive interference, the path difference must be an odd multiple of half wavelength. So, there will be dark fringes when the path difference is λ/2,3λ/2,5λ/2,7λ/2,9λ/2,11λ/2,13λ/2. So, 7 dark fringes are formed between O and P.

Diffraction:
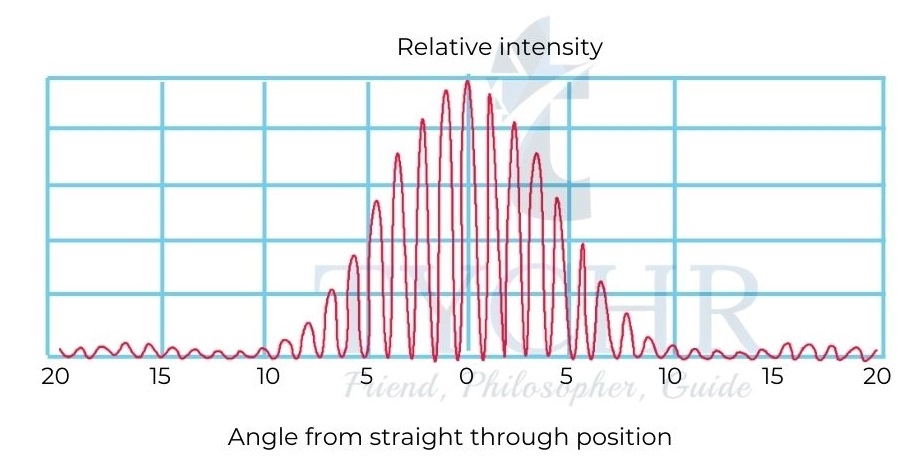
Diffraction is an application of interference. When a wave is passed through narrow gap or slit, whose dimensions are comparable to the wavelength of wave, the waves form a series of bright and dark fringes of varying intensity.
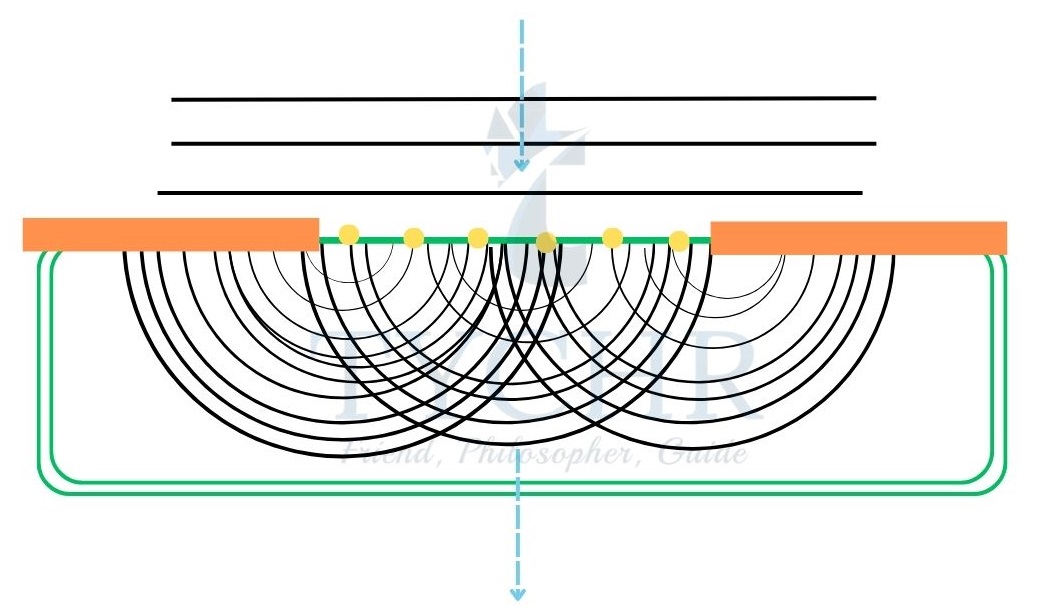
The plane waves travelling through the slit behave as if there were sources of secondary wavelets. The fringes are brightest and widest at the centre and the intensity and width decreases as we move away from centre.
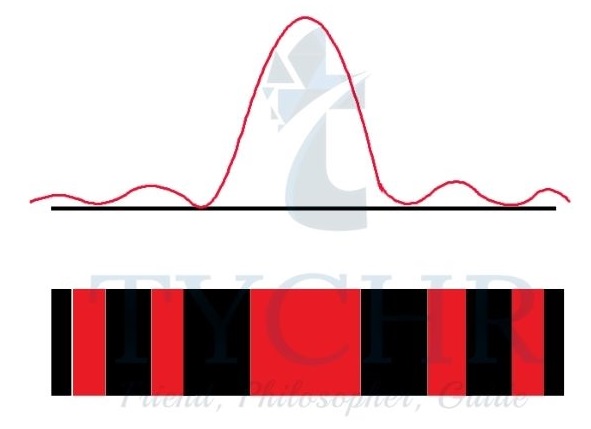
The angular position of minima is given by 𝜃 = 𝑛𝜆/𝑎.
Intensity with a double slit:
In the double slit experiment, the two slits produce diffraction pattern. So, the result is a combination of diffraction and interference. The distance between the maxima does not change but the intensity changes similar to a diffraction pattern.
Interference with multiple slits:
As the number of slits increase, the maxima and minima become sharper and more intense.
Dispersion:
The angle of refraction is different for different wavelengths of light. So, white light, being a combination of number of wavelengths, disperse into its constituent wavelengths when passed through a prism.
Resolution:
Rayleigh criteria: Two points are just resolved if the central maximum of first point falls on first minimum of second point. The angular position of first minimum is . This can be used to calculate if two spots are resolved or not.
Diffraction grating:
Diffraction gratings contain large number of equally spaced slits used to develop optical spectra. For a wavelength , the grating produces maxima at angles given by
𝑛𝜆 = 𝑑𝑠𝑖𝑛𝜃
Here d is the distance between slits in grating.
Diffraction grating resolvance:
The width of interference fringes produced from a diffraction grating is related to the number of lines on the grating.
The resolvance R of a grating is defined as 𝜆/∆𝜆= 𝑚𝑁, where λ is the wavelength of light and ∆λ is the smallest distance to the next resolvable wavelength. m is the order of spectrum and N is the number of slits.
Reflection of light off thin films:
Consider a soap film of thickness t, the refractive index of which is n and the wavelength of light in air incident on it is λ.

Doppler effect in light:
The change in frequency of a light wave is ∆𝑓 = (𝑣/𝑐)f0
f0 is the original frequency,
v is the relative velocity of observer and source,
c is the speed of light in vacuum.
Water waves:
Water waves follow all laws and exhibit all properties exhibited by light like reflection, refraction, interference and diffraction.
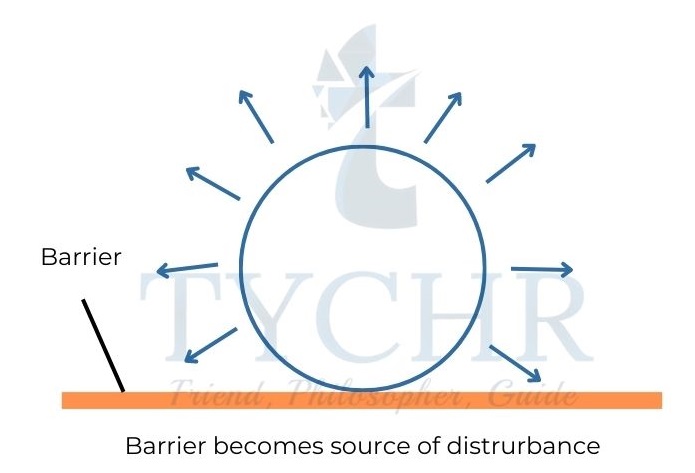
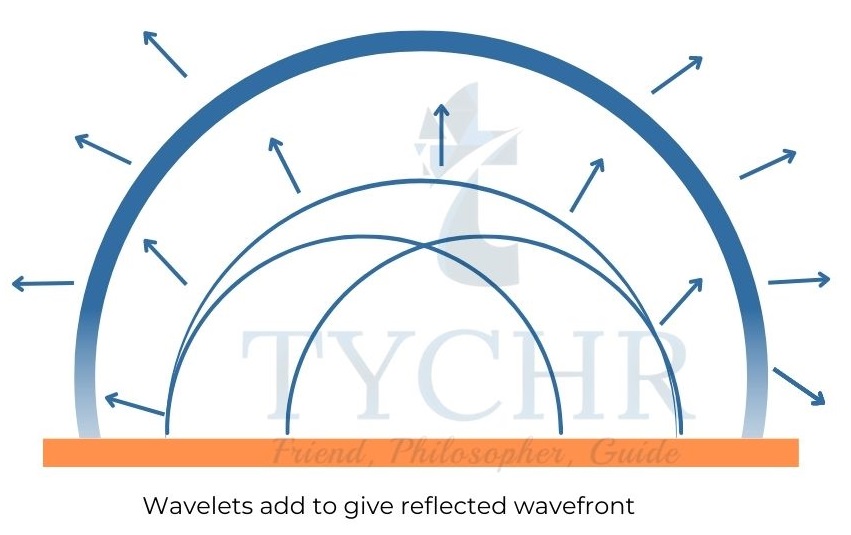
Wave propagation: A wave front can be thought of as being made up of infinite new centres of disturbance. The successive wave front is made up of the sum of the wavelets from the disturbances of these new sources.
Reflection of water wave: When a wave hits a barrier, the wave behaves as if a similar wave is coming from the barrier in the opposite direction.
Refraction, diffraction and interference are similar to that of light.
Doppler effect in sound:
The frequency of a moving source seems to change for an observer at rest and it also happens when the observer is moving and the source is at rest.
For a moving source,
The observed frequency is 𝑓𝑐 =𝑐𝑓0/(𝑐−𝑣), when the source moves with a velocity v towards the observer.
For a moving observer,
The observed frequency is 𝑓𝑐 = (𝑐+𝑣)𝑓0/𝑐, when the observer approaches the source with a velocity v.
Standing waves
Boundary conditions:
When a wave gets reflected off a fixed boundary (or a medium of higher optical density), it suffers a phase change of 180˚.
When a wave gets reflected off a free boundary (or a medium of lower optical density), there is no change in phase of the wave.
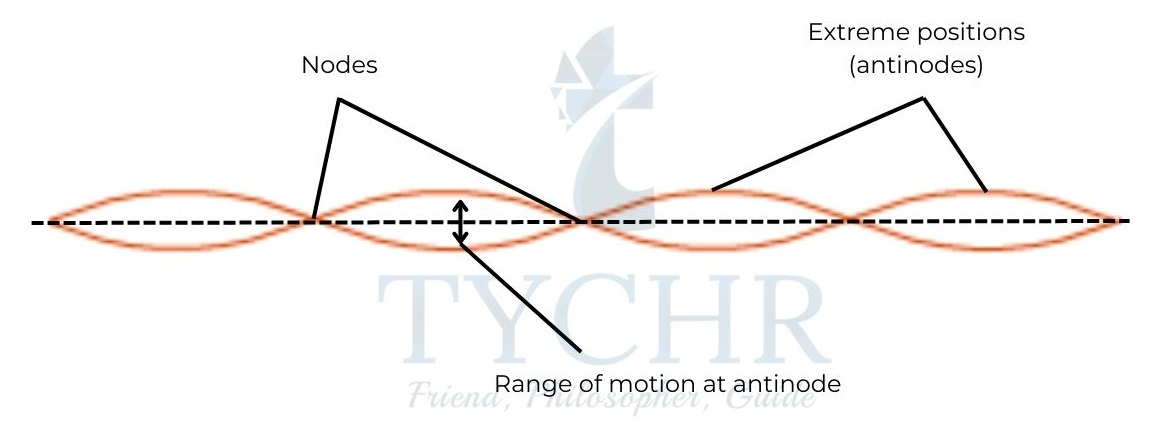
Standing waves:
Standing waves are formed when two waves of equal amplitude, frequency travelling with same speed in opposite direction are super imposed.
In such waves, the positions of crests and troughs do not change with time.
Nodes are the points at which the displacement is always zero.
Anti-nodes are the points at which the displacement varies from a maximum in one direction to a maximum in another direction.
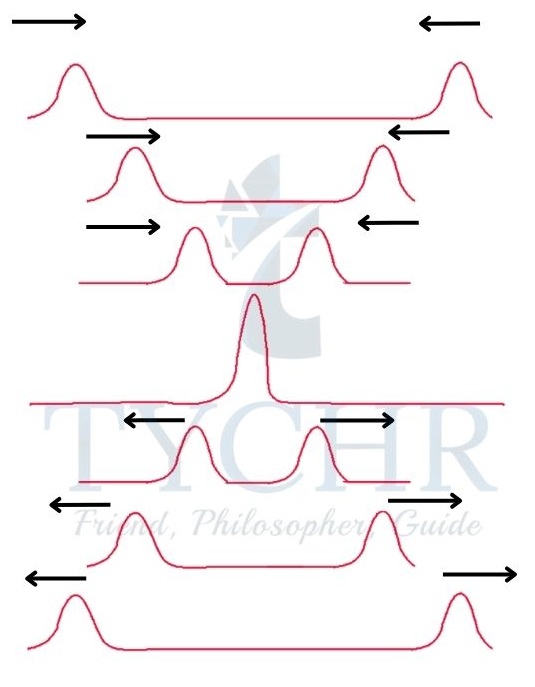
Harmonics on a string:
A string is tied at one end and connected to a vibration generator at another end. When the string is excited from zero frequency, a standing wave with a single loop is formed at a particular frequency with half the wavelength. This is called the first harmonic. At n times the frequency of the first harmonic, the nth harmonic is formed with n loops.
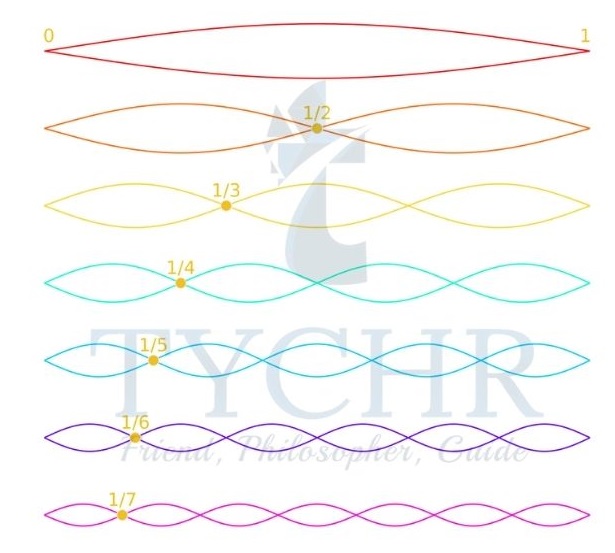
E.g.: A string is attached between two rigid supports and is made to vibrate at its first harmonic frequency f. The diagram shows the displacement of the string at t = 0.

(a) Draw the displacement of the string at time
(i) t = 1/4f

(ii) t = 1/2f

(b) The distance between the supports is 1.0m. A wave in the string travels at a speed of 240 ms-1. Calculate the frequency of the vibration of the string.
Answer.
a) i) The time that has passed is t = 1/4f = T/4
This is quarter of a cycle.
ii) The time that has passed is t = 1/2f =T/2
This is half of a cycle.
b) The wave equation is v=fλ.
Here λ = 2L = 2m, and v = 240ms-1.
So, the frequency is 𝑓 = 𝑣/λ = 240 /2 = 120Hz
Harmonics in a pipe:
In a pipe, if one end is open, the other end can be either open. The waves reflecting off a closed end form a node at that end, while those reflecting off an open end form an antinode at that end.
The harmonics in a pipe are similar to those formed in string.
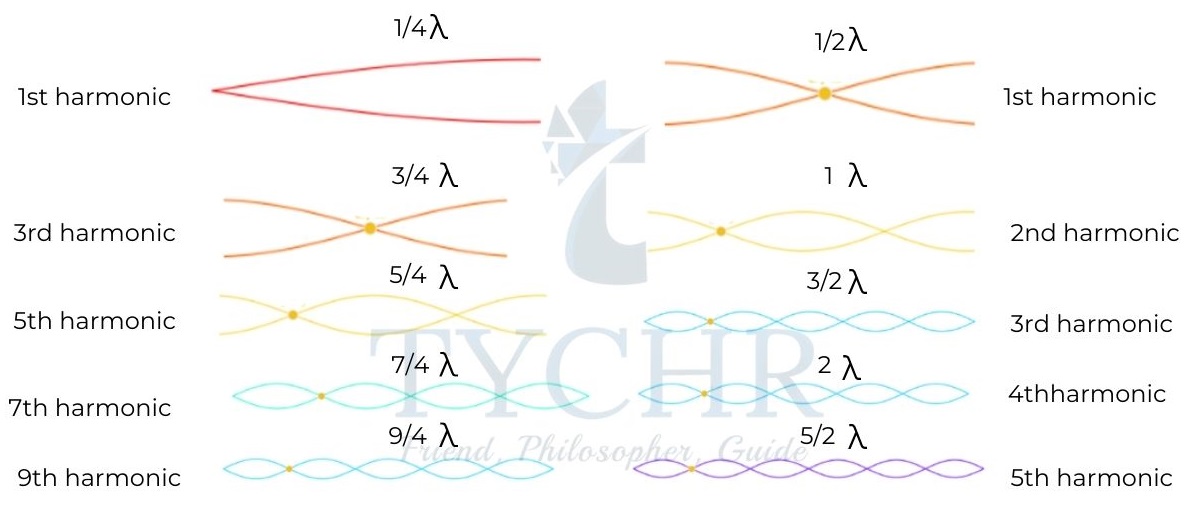
The first one shows harmonics with one end closed and the second one with both ends open.
E.g.: The frequency of the first harmonic emitted by an organ pipe that is closed at one end is f. What is the frequency of the first harmonic if both ends are open?
Answer.
The length of the pipe closed at one end with a wavelength is 𝜆/4=L. So, the wavelength is 4L.
When both ends are open, the wavelength is twice the length of pipe. So, the wavelength is 2L.
Since the wavelength is halved, the frequency will be doubled. The frequency will be 2f.

