Thermal Physics Theory Notes
Temperature and energy transfer
Heat:
Heat is a form of energy related to the kinetic energy of molecules.
Temperature and thermal equilibrium:
Temperature is the degree of hotness or coldness of a body. It is the gradient which decides the direction of heat flow.
- It is a scalar.
- SI unit is kelvin(K). More generally centigrade or Fahrenheit is used.
Two objects are said to be in thermal equilibrium if the two bodies are of the same temperature. Then, no heat flows between them.
Absolute temperature:
The temperature in kelvin scale is absolute temperature. At absolute zero temperature (0K), the molecular motion stops completely.
T(K) = T(˚C)-273.15
Heat transfer:
Heat transfer can happen in three ways
- Conduction: Conduction happens when the bodies are in contact. The vibrating molecules of a higher temperature body pass on the energy to lower temperature molecules. Metals are good conductors and gases are poor conductors of heat.
- Convection: This occurs in fluid. When heat is being supplied to a fluid, the density of the hotter part decreases (due to expansion) and moves to the upper part forcing the cooler part downwards. This flow of fluid is called convection current.
- Radiation: Through this process, the heat can directly be transferred without any medium or contact. This occurs by emission and absorption of infrared radiation.
Thermal capacity:
Thermal capacity of a body is the amount of heat required to raise its temperature by 1˚C.
Unit: J˚C-1 or JK-1.
If the temperature of a body changes by ∆T when Q amount of heat is supplied, its thermal capacity is s 𝐶 = 𝑄/∆T.
E.g.: How much heat is required to raise the temperature of a quantity of water from 20˚C to 100˚C if its thermal capacity is 5000JK-1.
Answer.
Rearranging the definition of thermal capacity
𝑄 = 𝐶 × ∆T = 5000 × (100 − 20) = 400kJ
E.g.: How much heat is lost from a block of metal if its temperature drops from 60˚ to 20˚C if its thermal capacity is 800JK-1.
Answer.
Heat lost = −𝐶∆T = 800 × (60 − 20) = 32𝑘J
Specific heat capacity:
The specific heat capacity of a material if the amount of heat required to raise the temperature of unit mass of substance by 1˚C.
Unit is Jkg-1K-1 or Jkg-1 ˚C-1.
If the temperature of a body of mass m changes by ∆T when Q amount of heat is supplied, its thermal capacity is 𝑐 = 𝑄/m∆T

E.g.: How much heat will be required to heat 300g of water from 20˚ to 60˚C if the specific heat of water is 4200 Jkg-1K-1.
Answer.
𝑐 = 𝑄/m∆T
𝑄 = 𝑚𝑐∆T = 0.3 × 4200 × (60 − 20) = 50.4kJ
E.g.: A car of mass 1500 kg travelling at 20 ms-1 brakes suddenly and comes to a stop.
a) How much KE does the car lose?
b) If 75% of the energy is given to the front brakes, how much energy will they receive?
c) The brakes are made out of steel and have a total mass of 10 kg. By how much will their temperature rise if the specific heat of steel is 440 Jkg-1K-1?
Answer.
a) The KE of the car is s (1/2)𝑚𝑣2 =(1/2)× 1500 × 202 = 300𝑘J
b) 75% of 300 kJ is 225kJ.
c) From the definition of specific heat capacity,
Raise in temperature of brakes ∆𝑇 = 𝑄 /𝑚𝑐 = 225000 /440×10 = 51.13K
E.g.: A piece of iron of mass 0.133kg at temperature θ is transferred to 0.476kg of water at 16˚C. The temperature of water rises to 45˚C. The specific heat capacities of water and iron are 4200 Jkg-1K-1 and 540 Jkg-1K-1 respectively.
a) Find the energy transfer in terms of θ from iron.
b) Find the energy transferred to water.
c) Using your answers, determine θ.
Answer.
a) Energy lost by iron block = 𝑚𝑐∆𝑇 = 0.133 × 540 × (θ − 45) = 60 × (θ − 45)
b) Energy gained by water = 0.476 × 4200 × (45−16) = 5.8 × 104J
c) Assuming that no energy is lost,
60 × (θ − 45) = 58000
𝜃 = 1000˚C
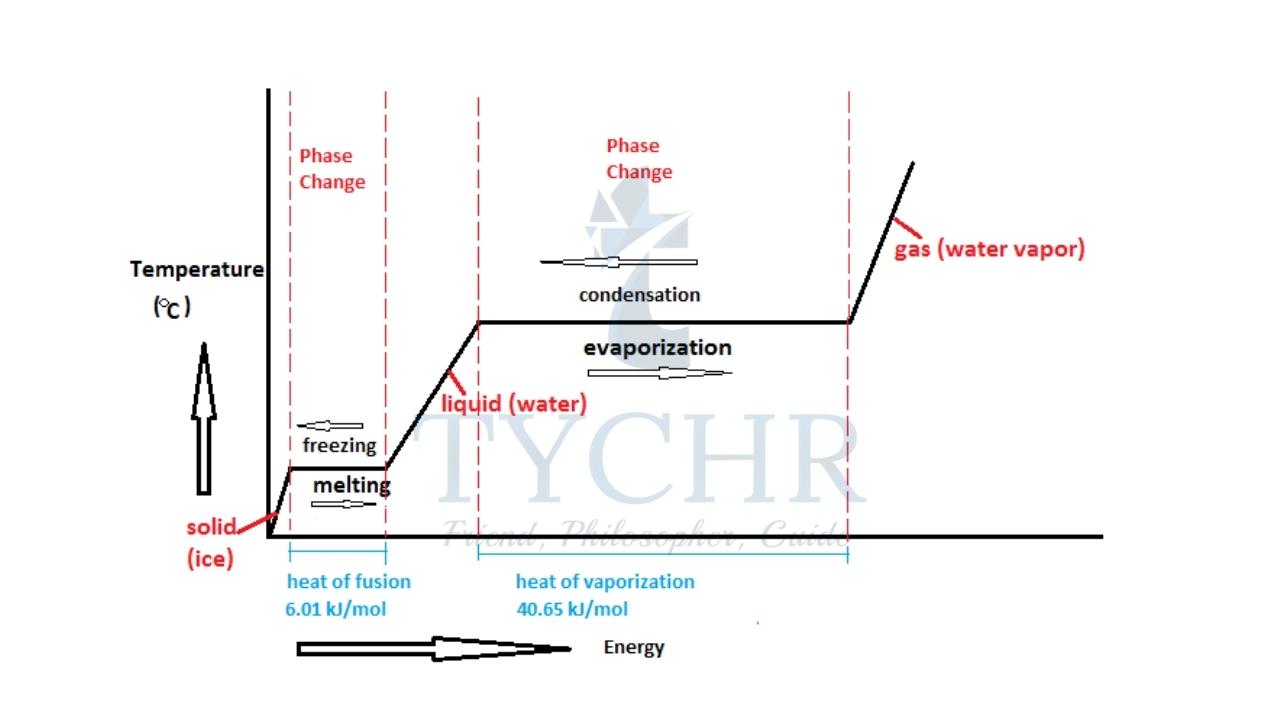
Phase change:
Phase change takes place at constant temperature. The heat transferred during this process deals with changing potential energy of molecules. The energy transferred per unit mass of substance to change its phase is called specific latent heat.
- Specific latent heat of vaporisation is the amount of heat required to convert unit mass of substance from liquid to gas at constant temperature.
- Specific latent heat of fusion is the amount of heat required to convert unit mass of substance from solid to liquid at constant temperature.
If Q is the amount of heat required for a substance of mass m for phase change,
Latent heat at 𝐿 = 𝑄/𝑚.
Graphical representation of phase change:
Consider a substance initially in solid state. Heat is supplied to the substance at a constant rate and the temperature of the substance is plotted against time.
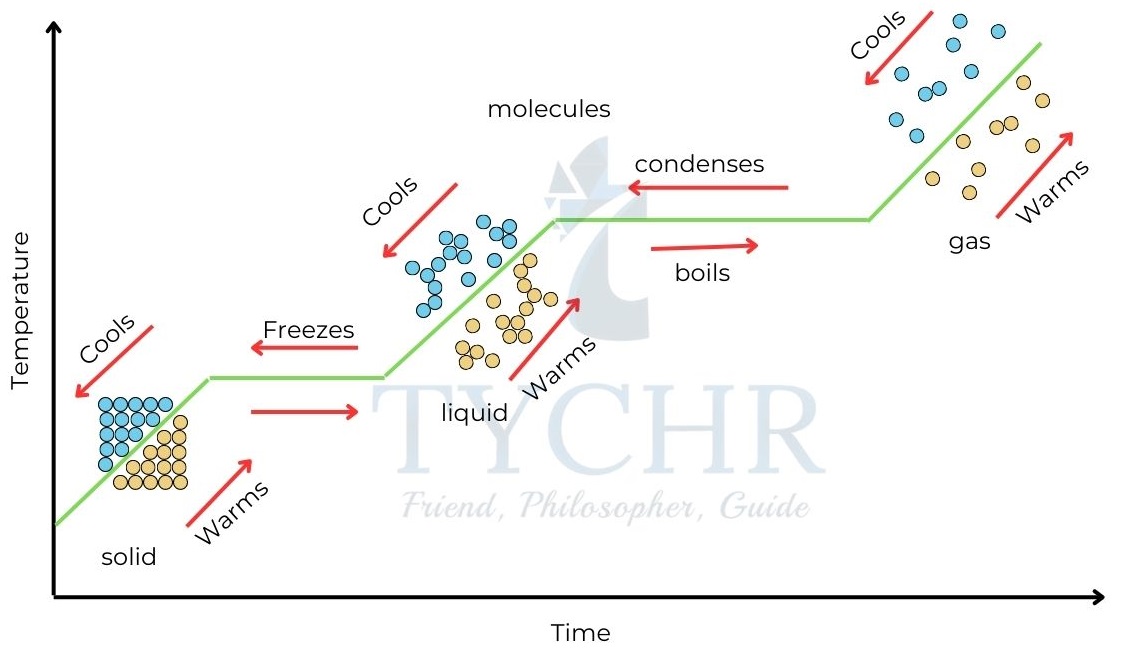
The regions of non-horizontal lines represent temperature change at corresponding states.
Horizontal lines represent phase change. They are horizontal because temperature does not change even though heat is supplied during phase change.
E.g.: How much energy is released when 500g of water is converted into ice at constant temperature if specific latent heat of fusion of water is 3.35×105 Jkg-1.
Answer.
From the definition of latent heat,
𝑄 = 𝑚𝐿 = 0.5 × 3.35 × 105 = 1.675 × 105J
E.g.: A heater is used to boil a liquid in a pan for a measured time.
The following data are available.
Power rating of heater = 25 W
Time for which liquid is boiled = 6.2 × 102 s
Mass of liquid boiled away = 4.1 × 10-2 kg
Use the data to determine the specific latent heat of vaporization of the liquid.
Answer.
The amount of heat supplied to water is 25 × 6.2 × 10−2 = 15.5𝑘𝐽
Latent heat of vaporisation = 𝑄/𝑚 = (15.5×103)/(4.1×10−2) = 3.8 × 105 𝐽𝑘𝑔−1
Modelling a gas
Avogadro’s hypothesis and mole:
Avogadro’s hypothesis states that equal volumes of all gases contain equal number of molecules at same temperature and pressure.
Mole is a unit for quantity of substance. It is equal to the number of atoms present in 12g of carbon-12 isotope. It is equal to 6.022 × 1023.
Molar mass of a substance is the mass of 1 mole of substance.
E.g.: 1 mole of carbon has a mass of 12g. How many atoms are present in 2g?
Answer.
One mole contains 6.022 × 1023 atoms.
2 grams is (1/6)th of a mole. So, it contains (1/6)× 6.022 × 1023 = 1.003 × 1023 atoms.
E.g.: The density of iron is 7874kgm-3. What is the volume occupied by one mole of iron if its molar mass is 55.85g?
Answer.
𝑉𝑜𝑙𝑢𝑚𝑒 = 𝑚𝑎𝑠𝑠/𝑑𝑒𝑛𝑠𝑖𝑡𝑦 = 0.05585 / 7874 = 7.093𝑐𝑚3
Ideal gas:
Few assumptions are made in developing theories for gases. These are
- The molecules are perfectly elastic.
- The molecules are perfect spheres.
- Molecules are identical.
- There are no forces between molecules. This implies that internal energy of gases is only due to kinetic energy and not due to potential energy.
- The molecules are very small. The volume occupied by molecules is negligible compared to the volume occupied by the gas.
Defining the state of gas:
Three variables are necessary and sufficient to completely describe the state of gas.
Volume: Volume of a gas is the volume of the container in which it is held.
Temperature: The temperature of gas is directly proportional to the average kinetic energy of gas molecules.
The total kinetic energy of N molecules of gas at temperature T is (3/2)𝑁𝑘T. Here k is the Boltzmann constant and has a value of 1.38 10-23JK-1.
Pressure: The pressure of a gas is the force exerted per unit area. It is a scalar and is uniform through the gas.
Gas laws:
Boyle’s law:
The pressure of a fixed amount of gas at constant temperature is inversely proportional to its volume.
𝑃 𝛼 (1/𝑉) 𝑎𝑡 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 T
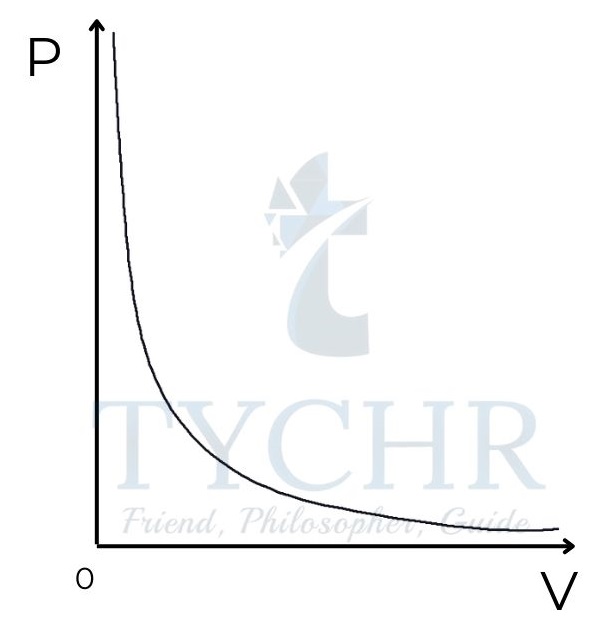
Graph of pressure against volume for a gas at constant temperature.
Charles law:
For a fixed amount of mass at constant pressure, the volume occupied by a gas is directly proportional to absolute temperature.
𝑉 𝛼 𝑇 𝑎𝑡 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 𝑝𝑟𝑒𝑠𝑠𝑢𝑟𝑒
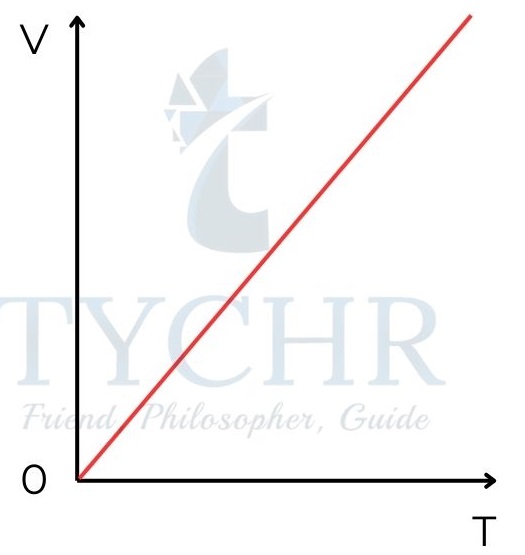
Graph of volume against temperature at constant pressure
Gay-Lussac’s law:
The pressure of a constant amount of gas contained with constant volume is directly proportional to the absolute temperature of gas.
𝑃 𝛼 𝑇 𝑎𝑡 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 𝑣𝑜𝑙𝑢𝑚𝑒
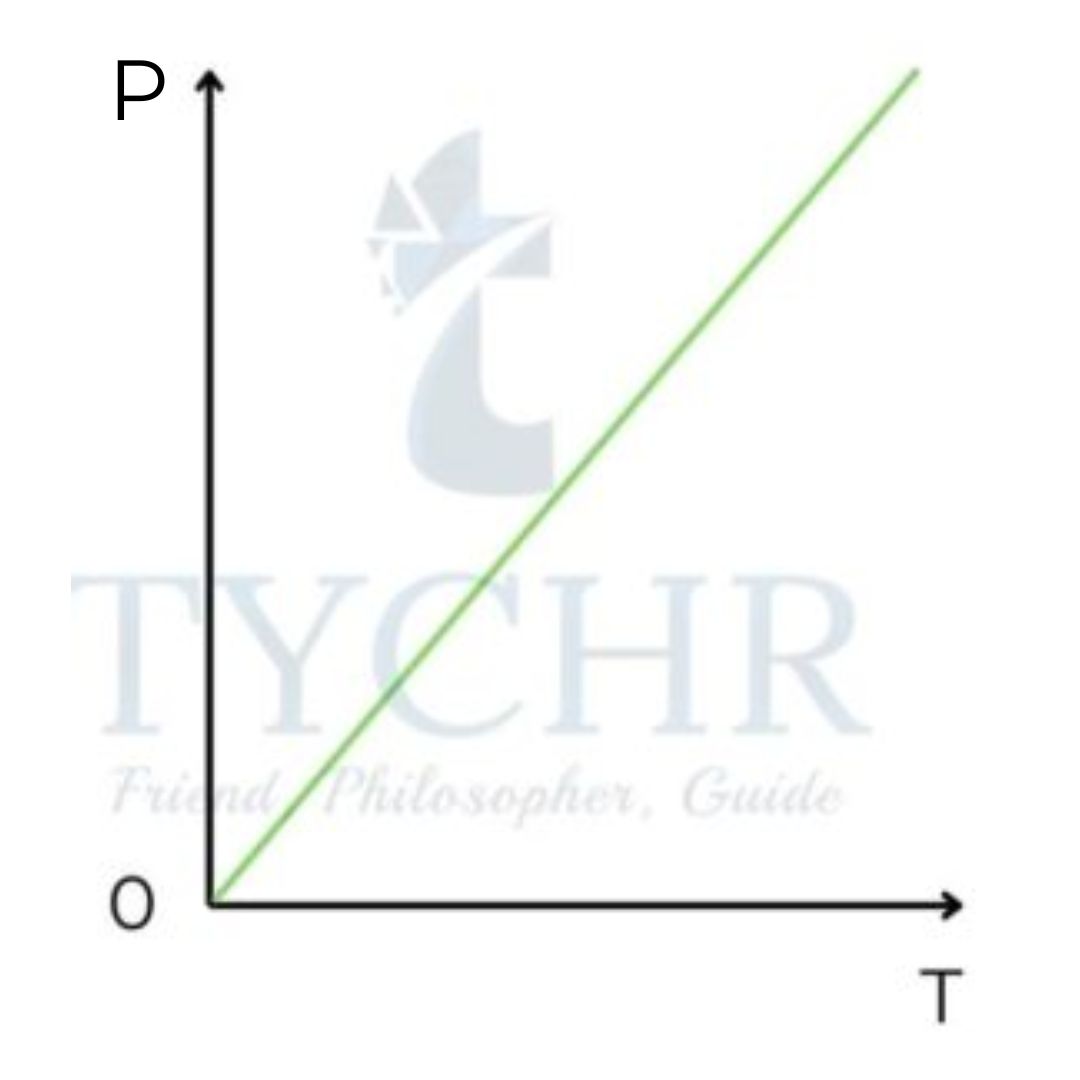
Graph of pressure against temperature at constant volume
Combining the three laws and Avogadro’s hypothesis, we get the ideal gas equation.
𝑃𝑉/𝑛𝑇 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 = 𝑅
𝑃𝑉 = 𝑛𝑅T
R is called universal gas constant and has a value of 8.314 J mol-1 K-1.
E.g.: The pressure of a gas inside a cylinder is 300 kPa. If the gas is compressed to half its original volume and the temperature rises from 27 °C to 327 °C, what will its new pressure be?
Answer.
Using the ideal gas equation, PV = nRT
(𝑃 × 0.5𝑉)/(327 + 273) =(300 × 𝑉)(27 + 273)
𝑃 = 1200𝑘𝑃𝑎
E.g.: Calculate the percentage change in volume of a fixed mass of an ideal gas when its pressure is increased by a factor of 2 and its temperature increases from 30 °C to 120 °C.
Answer.
𝑃𝑉/𝑇 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡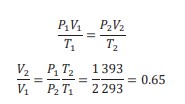
The volume of gas decreases by 35%.
Microscopic interpretation of gases:
Diffusion: It is the process through which gases from one place to another. The gas molecules collide with surrounding air molecules and move through out air.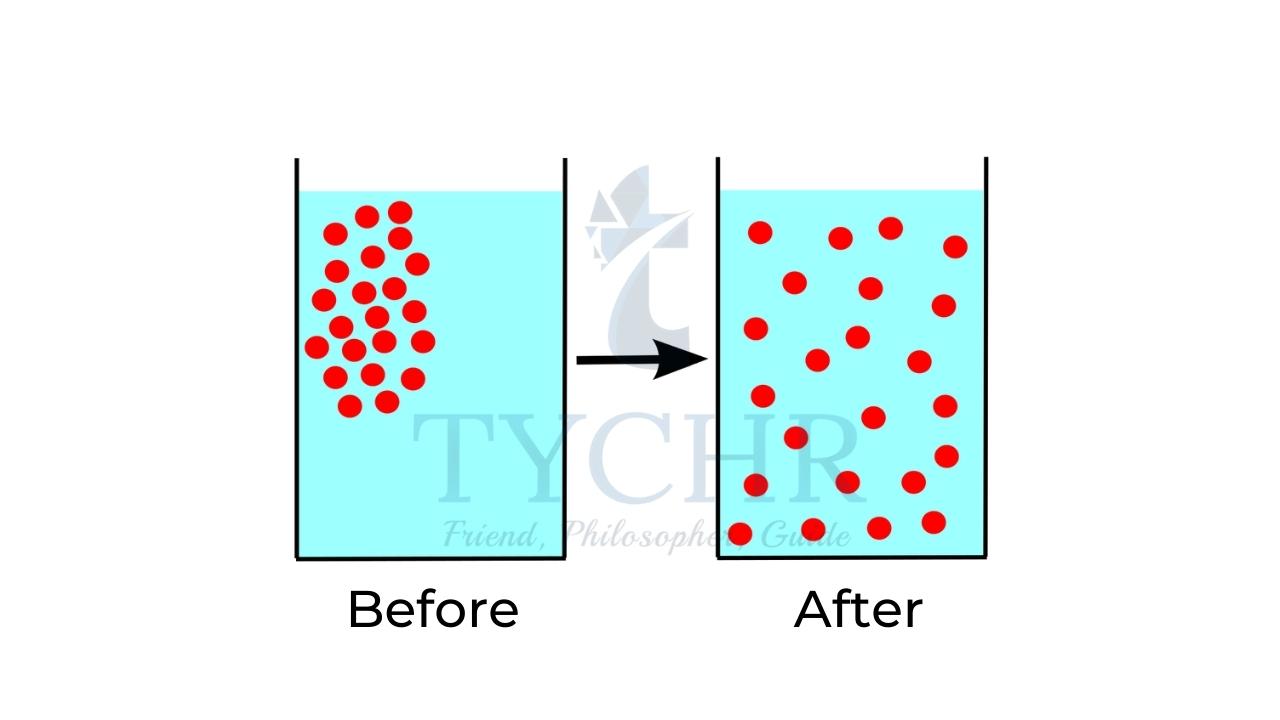
Brownian movement: Small particles like smoke or pollen grains move in shot straight lines of irregular pattern which can be observed through a microscope. This is due to bombardment of smoke particles by air molecules.
Root mean square speed of a gas: The root mean square is the mean velocity of the gas as a whole. For a group of n molecules,
𝑐 = √((∑𝑖=1n 𝑐𝑖2𝑛)/n)
The pressure of a gas is related to the root mean square speed as
𝑃 =(1/3)𝜌𝑐2
E.g.: Nitrogen gas is sealed in a container at a temperature of 320 K and a pressure of 1.01 × 105 Pa.
a) Calculate the mean square speed of the molecules.
b) Calculate the temperature at which the mean square speed of the molecules reduces to 50% of that in a). Mean density of nitrogen gas over the temperatures considered = 2 kgm-3
Answer.
a) 𝑐 = (3𝑃/𝜌) = (3×1.01×105)/1.2 = 25.3 × 105𝑚2𝑠−2
b) c2 α So, the mean square speed reduces to 50% at 50% of temperature – at 160K.

