50+ IB Maths AI IA Ideas
check out our results
Request Free Trial Class
Are you an IB Math student working on your IB Math AI Internal Assessment?
Tychr has curated a list of 50+ IB Maths IA ideas specifically designed for IB Math AI (Applications and
Interpretations) students. This list features 50+ specific IB Math IA AI ideas and topics that span a wide range of mathematical concepts, including calculus, algebra, geometry, statistics, and probability. Whether you’re in SL or HL, these ideas are tailored to help you craft a standout project. Plus, you’ll find Maths AI IA samples to guide you in structuring and presenting your work effectively.
From analyzing real-world scenarios to exploring advanced theoretical models, these IB Math IA AI ideas are perfect for students looking to create unique and high-scoring projects. With Tychr’s expert IB Math AI tutors, you’ll receive inspiration and personalized guidance to confidently tackle your IB Math IA. Explore the list now to find the perfect topic that matches your interests and academic goals!!
IB Math AI IA Ideas
1.) Employing Optimization To Minimize Amount Of Packaging Material
Mathematics:
Using mathematical concepts like differentiation and integration to derive generalized conditions that minimize the surface area and hence the packaging of these differently shaped goods (example: conical, cuboid and irregular shaped goods).
Procedure:
The actual surface area will be found using the existing dimensions. Then, the volume of a standard cylindrical shape is differentiated to find out if a minimized surface area exists. Once the minimum dimension values are found, the minimum surface area will be calculated. This is repeated for conical, cuboid, and irregular shaped goods.
Analysis:
Total wastage is calculated by subtracting the minimized surface area from the actual surface area.

IB Math AI SL IA Ideas
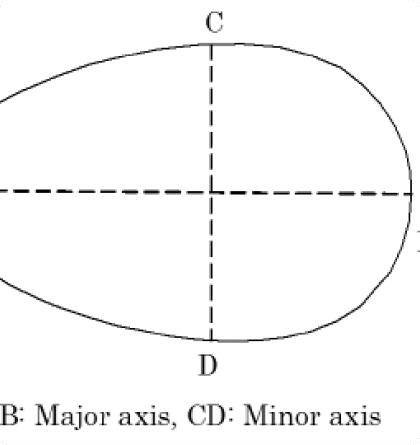
5.) Using Pringles to explore the formula of a hyperbolic paraboloid, determine the surface area and define the hyperbolic paraboloid parametrically
Mathematics:
Using mathematical concepts like differentiation and integration to calculate the surface area of a hyperbolic paraboloid such as a pringle.
Procedure:
Firstly, you would have to draw the pringles chip and then plot it on a graph. Then you must split it into different parts, and derive the equation. Calculate the surface area using integration.
Analysis:
This analysis is most important when it comes to the firm’s point of view. For instance, when manufacturing Pringles, one must optimize space and ingredients to ensure consumer satisfaction and reduce costs for the firm.

Download our Successful College Application Guide
Our Guide is written by counselors from Cambridge University for colleges like MIT and other Ivy League colleges.
To join our college counseling program, call at +918825012255

IB Tutoring Recent Blogs
Give our blog a read for anything you need















