IB Physics SL Paper 2 Question Bank
The IB Physics SL Paper 2 Question Bank is a great resource for students studying for their IB Physics SL exam. The question bank contains a wide range of questions, from easy to difficult, covering all the topics in the IB Physics SL syllabus. This makes it an essential study tool for all IB Physics SL students. The question bank is regularly updated with new questions, so it’s always up-to-date with the latest changes to the syllabus. There are also detailed answer explanations for every question, so you can understand why each answer is correct.
Time: 1 hour 15 minutes
Instructions to candidates
- Answer all questions
- Answers must be written within the answer boxes provided.
- A calculator is required for this paper.
- A clean copy of the physics data booklet is required for this paper.
- The maximum mark for this examination paper is [50 marks].
Answer all questions. Answers must be written within the answer spaces provided.
1.)
a.) A car of mass 1000 kg is traveling on a straight, level road at a speed of 20 m/s. The driver suddenly applies the brakes, causing the car to come to a stop over a distance of 50 m. Calculate the average force exerted on the car by the brakes during the braking process.
i.) What is the initial kinetic energy of the car?
Answer:
The initial kinetic energy of the car is given by K = (1/2)mv², where m is the mass of the car and v is its initial speed. Substituting the given values, K = (1/2)(1000 kg)(20 m/s)² = 200000 J.
ii.) How much work is done by the brakes in bringing the car to a stop?
Answer:
The work done by the brakes in bringing the car to a stop is equal to the change in kinetic energy of the car, which is K = 200000 J. Therefore, the work done by the brakes is 200000 J.
b.) A block of mass 2 kg is initially at rest on a horizontal surface. A horizontal force of 10 N is applied to the block, causing it to accelerate uniformly to the right. The coefficient of kinetic friction between the block and the surface is 0.2. Calculate the acceleration of the block.
Answer:
The net force on the block is given by Fnet = ma, where Fnet is the net force, m is the mass of the block, and a is its acceleration. The force of kinetic friction is fk = μkN, where μk is the coefficient of kinetic friction and N is the normal force. The normal force is equal to the weight of the block, N = mg, where g is the acceleration due to gravity. Therefore, the net force is Fnet = F – fk = ma, or 10 N – (0.2)(2 kg)(9.8 m/s²) = (2 kg)a. Solving for a, we get a = 3.02 m/s².
c.) A projectile is launched from the ground with an initial speed of 30 m/s at an angle of 45° above the horizontal.
i.) What is the maximum height reached by the projectile?
Answer:
The maximum height reached by the projectile is given by H = (v²sin²θ)/(2g), where v is the initial speed of the projectile, θ is the launch angle, and g is the acceleration due to gravity. Substituting the given values, H = (30 m/s)²sin²45°/(2(9.8 m/s²)) = 45.9 m.
ii.) How far from the launch point does the projectile land?
Answer:
The range of the projectile is given by R = (v²sin2θ)/g, where θ is the launch angle. Substituting the given values, R = (30 m/s)²sin(2×45°)/9.8 m/s² = 183 m.
iii.) What is the time of flight of the projectile?
Answer:
The time of flight of the projectile is given by t = (2v sinθ)/g. Substituting the given values, t (2(30 m/s)sin45°)/9.8 m/s² = 4.86
d.) A simple pendulum consists of a bob of mass 0.1 kg attached to a light string of length 0.5 m. The pendulum is pulled to one side to an angle of 10° and released from rest. Calculate the period of the pendulum.
Answer:
The period of a simple pendulum is given by T = 2π√(L/g), where L is the length of the string and g is the acceleration due to gravity. Substituting the given values, T = 2π√(0.5 m/9.8 m/s²) = 1.43 s.
2.)
a.) Describe the basic principle of an electric motor.
Answer:
An electric motor converts electrical energy into mechanical energy. It works on the principle of magnetic fields exerting forces on current-carrying conductors.
i.) Explain how a force is exerted on a current-carrying conductor in a magnetic field.
Answer:
When a current-carrying conductor is placed in a magnetic field, a force is exerted on it that is perpendicular to both the magnetic field and the direction of current flow. This is known as the motor effect.
ii.) State the factors that affect the size of the force on a current-carrying conductor in a magnetic field.
Answer:
The size of the force on a current-carrying conductor in a magnetic field depends on the strength of the magnetic field, the current flowing through the conductor, and the length of the conductor in the magnetic field.
b.) A simple electric motor consists of a rectangular coil of wire, a commutator, and a permanent magnet. The coil is made up of 200 turns of wire and measures 0.10 m by 0.20 m. The magnet has a flux density of 0.15 T and is placed so that the coil can rotate freely around its axis. When a current of 0.50 A flows through the coil, it experiences a torque of 0.018 N m. Calculate:
i.) the magnetic flux passing through the coil
Answer:
The magnetic flux passing through the coil can be calculated using the formula Φ = BAN, where Φ is the magnetic flux, B is the magnetic field strength, A is the area of the coil, and N is the number of turns in the coil.
Plugging in the given values, we get: Φ = (0.15 T)(0.10 m)(0.20 m)(200) = 0.06 Wb.
ii.) the force on each side of the coil
Answer:
The force on each side of the coil can be calculated using the formula F = BIL, where F is the force, B is the magnetic field strength, I is the current flowing through the coil, and L is the length of the side of the coil.
Plugging in the given values, we get: F = (0.15 T)(0.50 A)(0.10 m) = 0.0075 N. Therefore, the force on each side of the coil is 0.0075 N.
iii.) the maximum torque that the motor can produce
Answer:
The maximum torque that the motor can produce is given by the formula T = Fd, where T is the torque, F is the force on each side of the coil, and d is the distance between the sides of the coil. Plugging in the given values, we get: T = (0.0075 N)(0.20 m) = 0.0015 Nm.
c.)
i.) Suggest one way to increase the torque of the motor.
Answer:
One way to increase the torque of the motor is to increase the strength of the magnetic field.
ii.) Explain why increasing the number of turns in the coil would increase the torque.
Answer:
Increasing the number of turns in the coil would increase the torque because it would increase the magnetic flux passing through the coil, which in turn would increase the force on each side of the coil. This is because the force is directly proportional to the magnetic field strength and the number of turns in the coil.
d.) State two advantages and two disadvantages of using an electric motor instead of a petrol engine to power a car.
Answer:
Advantages of using an electric motor instead of a petrol engine to power a car include:
- Electric motors are more energy-efficient, which means they require less fuel or energy to produce the same amount of power as a petrol engine.
- Electric motors produce less pollution and greenhouse gas emissions than petrol engines, which makes them more environmentally friendly.
Disadvantages of using an electric motor instead of a petrol engine to power a car include: - Electric cars can have limited driving range, which means they may not be suitable for long-distance travel.
- Electric cars can be more expensive to purchase than petrol-powered cars, although this cost may be offset by lower fuel and maintenance costs over time.
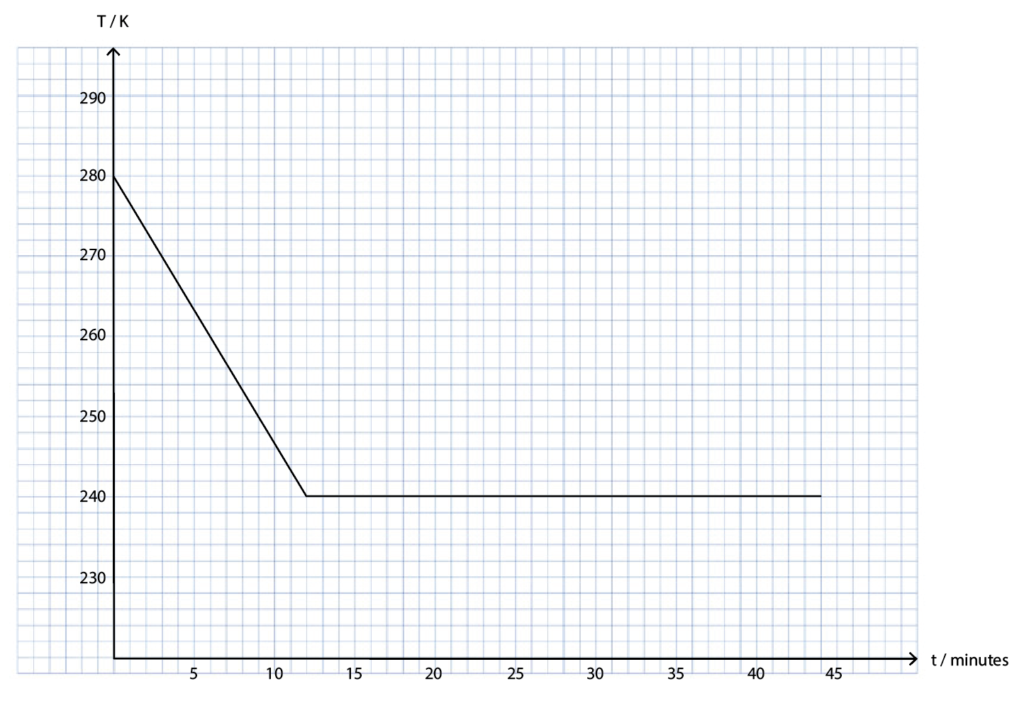
4.) A sample of a normal cooking oil is placed inside a freezer that transfers thermal energy from the sample at a constant rate. The initial state of this oil is liquid. The graph below shows how the temperature of the oil varies with time.
 The following data is given to you:
The following data is given to you:
Mass of the sample: 0.25 kg
Specific latent heat of fusion of the oil: 117 kJ/kg
Rate of thermal energy transfer: 10 W
a.)
i.) Calculate the thermal energy that was transferred from the oil during the first 12 minutes
Answer
10 x 12 x 60 = 7200 Joules
ii.) Estimate the specific heat capacity of the oil when it is in its liquid phase and include an appropriate unit
Answer
Q = mcΔT
7200=0.25 ×c ×(280-240)
c = 7200/(0.25×40)= 720 J/kg
b.) The oil sample begins to freeze amidst the process of the thermal energy transfer. Using the concept molecular model of matter, explain why a constant temperature is maintained during the freezing process.
Answer
When the freezing process happens, intermolecular bonds are formed and when these bonds are formed the process releases energy. Another explanation could be that the intermolecular potential energy decreases and the difference is transferred as heat. While this happens, the average kinetic energy of the molecules does not change. Since the temperature is associated with a change in kinetic energy and there is no change in kinetic energy, the temperature is constant during the freezing process.
c.) Calculate the mass of the oil that remains unfrozen after 44 minutes.
Answer
Mass of the frozen oil = (7.2×103)/(117×103 )=0.06 kg
Therefore, the unfrozen mass = 0.32 kg – 0.06 kg = 0.26 kg
4.)
a.)
i.) Define specific heat capacity and state its SI units.
Answer
The specific heat capacity of a substance is the amount of heat energy required to raise the temperature of 1 kg of the substance by 1 K. Its SI units are J kg⁻¹ K⁻¹.
ii.) A copper block of mass 200 g is heated from 20°C to 50°C. Calculate the energy absorbed by the block if the specific heat capacity of copper is 387 J kg⁻¹ K⁻¹.
Answer:
Here,
m = 0.2 kg (mass of copper block)
ΔT = (50 – 20)°C = 30 K (change in temperature)
c = 387 J kg⁻¹ K⁻¹ (specific heat capacity of copper)
Energy absorbed = mcΔT = 0.2 x 387 x 30 = 2322 J
b.) State the first law of thermodynamics and explain its significance.
Answer:
The first law of thermodynamics states that energy cannot be created or destroyed, only converted from one form to another. This law is significant as it forms the basis for the study of thermodynamics, and allows us to calculate the energy changes that occur during various processes.
c.) A gas is compressed from a volume of 2.5 L to 1.0 L against a constant external pressure of 3.0 atm. The initial pressure of the gas is 1.0 atm.
i.) Calculate the work done by the gas during the compression process.
Answer:
The work done by the gas is given by the expression W = -PΔV, where ΔV is the change in volume and P is the external pressure. Here,
ΔV = 2.5 L – 1.0 L = 1.5 L = 0.0015 m³ (change in volume)
P = 3.0 atm = 303750 Pa (pressure)
W = -PΔV = -303750 x 0.0015 = -456.56 J (work done)
ii.) Calculate the change in internal energy of the gas if the temperature remains constant.
Answer:
Since the temperature remains constant, the change in internal energy is zero.
d.) Define thermal equilibrium and explain why it is an important concept in thermodynamics.
Thermal equilibrium is the state in which two bodies in contact with each other have the same temperature and there is no net flow of heat energy between them. This concept is important in thermodynamics as it allows us to determine the direction of heat flow during various processes, and helps us to understand the behavior of different systems.
5.) There are 2 loudspeakers, X and Y that have the same amplitude at a frequency of 900 Hz. There is a Point P that is located 24.2 m from Speaker X and 26.7 m from Speaker Y. The speed of sound is 340 m/s.
a.) Determine the minimum sound intensity heard at Point P round to 2 significant figures
Answer:
Wavelength = Speed of sound/frequency of the wave
Wavelength = 340/900 = 0.3777 m
To find the sound intensity, the path difference needs to be found.
Therefore, 26.7 – 24.2 = 2.5 m
Intensity = Path difference/wavelength
Intensity = 2.5 / 0.37777 = 6.6177 = 6.6 λ
b.) Define the amplitude and frequency of a wave
Answer:
Amplitude is the distance between the resting position and the maximum displacement of the wave. Frequency is the number of waves passing by a specific point per second.
6.)
a.) A proton moves perpendicular to a uniform magnetic field of magnitude 0.8 T with a velocity of 5.0 × 106 m/s. Calculate the magnitude of the force acting on the proton.
i.) What is the direction of the force on the proton?
Answer:
The direction of the force on the proton is perpendicular to both the velocity vector and the magnetic field vector, according to the right-hand rule.
ii.) What will be the radius of the circular path followed by the proton?
Answer:
The radius of the circular path followed by the proton can be calculated using the equation F = Bqv, where F is the magnitude of the force, B is the magnetic field strength, q is the charge of the particle, and v is the velocity of the particle. Rearranging the equation to solve for the radius, we get r = mv/qB, where m is the mass of the particle. Plugging in the values given, we get r = 0.015 m.
b.) A charged particle enters a uniform magnetic field at an angle of 30° to the field direction. If the particle moves in a circular path with a radius of 0.15 m and a frequency of 60 Hz, calculate:
i.) The magnetic field strength
Answer:
Using the equation F = Bqv, we can solve for the magnetic field strength: B = F/qv. We know that F = mv2/r, so plugging in the given values and solving for B, we get B = 0.11 T.
ii.) The speed of the particle
Answer:
The speed of the particle can be calculated using the formula v = 2πr/T, where T is the period of the motion. We know that T = 1/f, so plugging in the given values, we get v = 942 m/s.
iii.) The charge of the particle
Answer:
Using the equation F = Bqv, we can solve for the charge of the particle: q = F/Bv. Plugging in the given values, we get q = 3.6 × 10-19 C.
c.) Explain why the motion of a charged particle in a uniform magnetic field is circular.
Answer:
The motion of a charged particle in a uniform magnetic field is circular because the magnetic force is always perpendicular to the velocity vector, which causes the particle to change direction but not speed. This results in a circular path, as the particle continually changes direction due to the magnetic force.
7.) This question is regarding atomic physics
a.) Rutherford made a model based on the results of the alpha particle scattering experiment. Describe Rutherford’s model.
Answer
The positive charge and most of the mass of an atom is concentrated in an extremely small volume. He called this region of the atom a nucleus. Rutherford’s model proposed that the negatively charged electrons surround the nucleus of an atom. He also claimed that the electrons surrounding the nucleus revolve around it with very high speed in circular paths. He named these circular paths as orbits.
b.) Explain what the binding energy of a nucleus means
Answer
Nuclear binding energy is the energy required to separate an atomic nucleus completely into its constituent protons and neutrons, or, equivalently, the energy that would be liberated by combining individual protons and neutrons into a single nucleus.
c.) Outline why quantities such as binding energy and atomic mass are expressed non-SI units
Answer
It is because these quantities would be extremely small
8.) Water is stored in a dam at a depth of 30 m in a pumped storage hydroelectric system.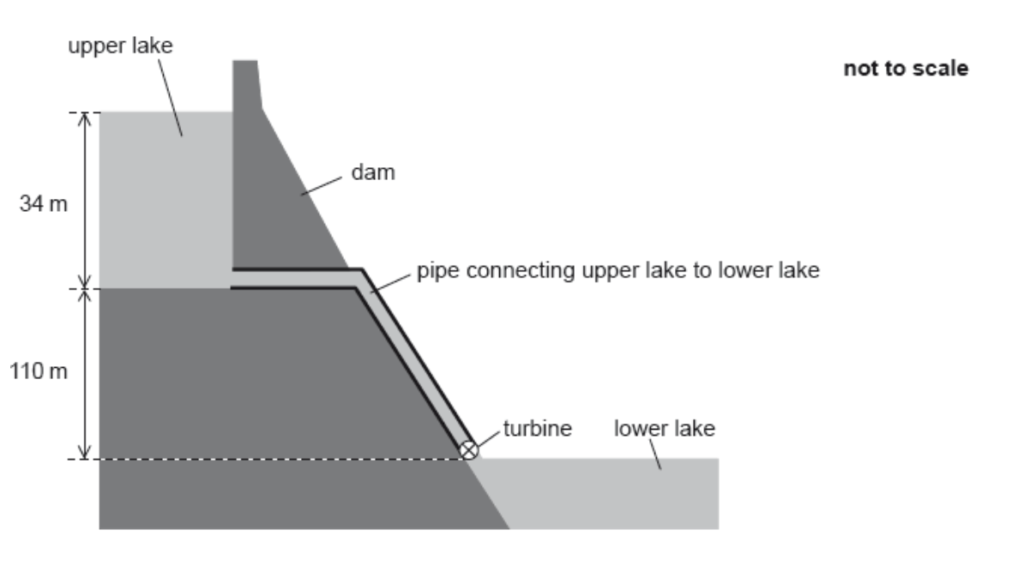
The water that leaves the upper lake goes down at a vertical distance of 92 m and causes the turbine to rotate as it goes into the lower lake. The water that flows out of the upper lake, flows at a rate of 1.6 x 105 m3 per minute. The density of the water 1.0 x 103 kg/m3.
a.)
i.) Estimate a value for the specific energy of water and include appropriate units.
Answer
Estimating that the water is continuously being released into the lower lake, we will assume half the height of the water of the lake which is 15m. Therefore, adding it to the height of the dam, we have an average height of 107m.
Specific energy = mgh/m = gh = 9.81×107 = 1049.67 ∼ 1.05×103 Jkg-1
ii.) Show that the average rate in which the gravitational potential energy of the water decreases is approximately 2.8 GW.
Answer
Average mass per second of the water leaving the dam is calculated by
((1.6×105)/60) × 103 = 2.666 ×106 kgs(-1) ∼ 2.67 × 106 kgs(-1)
Rate of decrease in the gravitational potential energy is given by:
2.67×106 ×9.81×107=2.8×109W = 2.8 GW
iii.) The storage system has an electrical power of 1.6 GW. Using this value, determine the efficiency of the storage system.
Answer
1.6/2.8=0.5714 ∼57%
b.) Once the upper lake is emptied into the lower lake, the water needs to circulate back to the upper lake to refill it. This process requires energy. Suggest how the operators of this storage system can still make a profit.
Answer
The water can be pumped back up to the upper lake when the demand for electricity is low or when the cost of the electricity is lesser.


