Table of Contents [hide]
Unlocking the Secrets of Data Distribution: Analyzing a Right-Skewed Histogram
Have you ever found yourself staring blankly at a histogram, wondering what secrets it holds? Don’t worry, you’re not alone! Histograms are powerful visual tools that help us understand the distribution of data. And today, we are diving deep into one particular type – the right-skewed histogram.
But what exactly is a right-skewed histogram? Why does it matter? And how can we interpret its patterns to unveil valuable insights? Join me as we embark on an exciting journey of exploration and discovery in the world of data analysis. Get ready to unravel the mysteries behind this fascinating distribution pattern and discover its significance. So buckle up, because things are about to get skewed in all the right ways!
Understanding Histograms and Skewness
When it comes to analyzing data, histograms are like the Sherlock Holmes of statistics. They provide us with a visual representation of how our data is distributed, allowing patterns and insights to emerge. But what exactly is skewness, and why does it matter in the world of histograms?
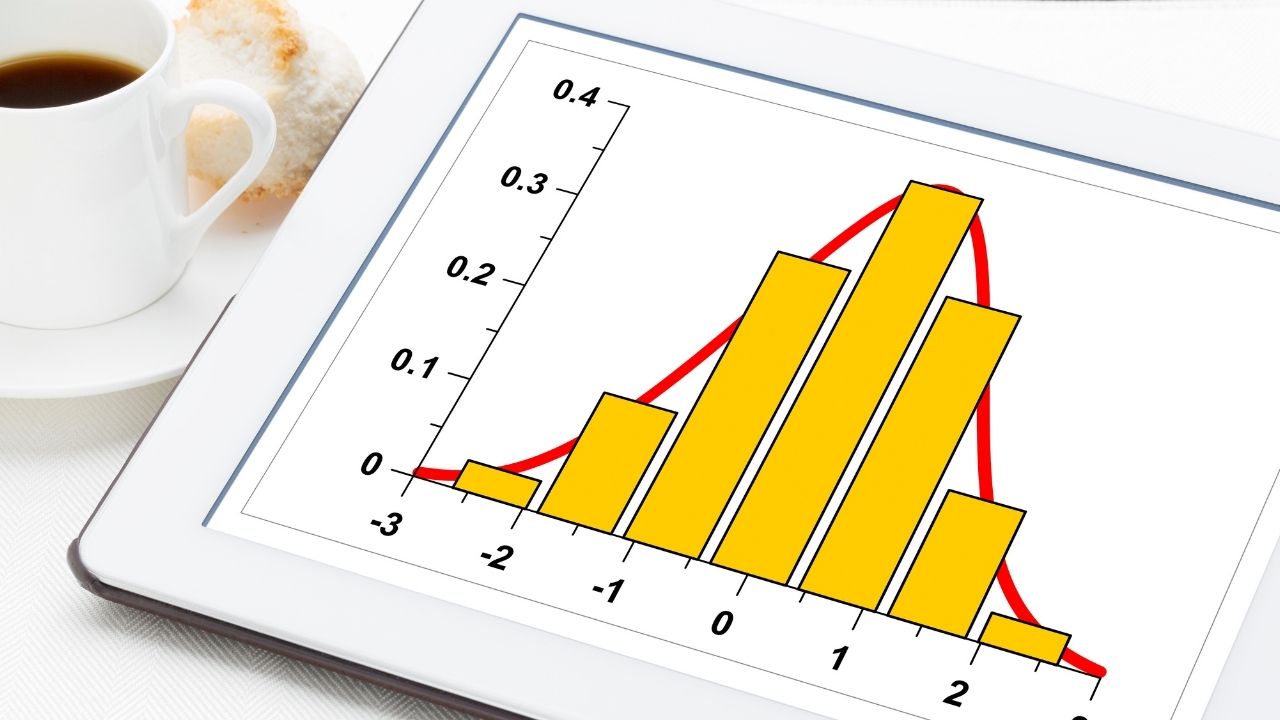
Skewness refers to the asymmetry or lack thereof in a dataset’s distribution. It tells us whether our data leans towards one side more than the other. When we talk about right-skewed histograms, we’re referring to datasets where the majority of values lie on the left side while a few extreme values stretch out towards the right.
Understanding skewness is crucial because it helps us interpret and draw conclusions from our histogram graphs accurately. By identifying whether our data is skewed or not, we can make informed decisions about how to analyze and interpret our findings.
So next time you encounter a histogram with an elongated tail stretching towards the right side, remember that you’re dealing with a right-skewed distribution! Strap on your detective hat as we delve deeper into this intriguing pattern and uncover its implications for data analysis.
Also read: Continental Breakfast Meaning: Exploring the Origins and Components of a Morning Meal
What is a Right-Skewed Histogram?
A right-skewed histogram, also known as a positively skewed histogram, is a graphical representation of data that shows the distribution of values in a dataset. In this type of histogram, the tail on the right side extends further than the tail on the left side.
To understand what this means visually, imagine looking at a mountain range from afar. If one peak is higher and steeper than the other peaks, it indicates a right-skewed distribution. This suggests that there are more occurrences of lower values and fewer occurrences of higher values in your dataset.
Why does skewness matter? Well, it provides insight into how your data is distributed and helps identify patterns or trends within it. By analyzing a right-skewed histogram, you can gain valuable information about your dataset’s characteristics and make informed decisions based on these insights.
The shape of a right-skewed histogram usually occurs when extreme outliers pull the mean towards them. These outliers have larger values compared to most observations in your data set and can significantly impact any statistical analysis performed on it.
Understanding why your data has this skewness allows you to interpret its implications correctly. For example, if you’re examining income levels among individuals and notice that there’s an extended tail towards high-income earners in your right-skewed histogram, you might deduce that only few people earn considerably more than others.
Analyzing histograms plays an essential role in fields such as finance, economics, healthcare management – virtually any discipline where quantitative analysis is required. By accurately interpreting histograms with their specific skewness patterns like those found in right-skew distributions – professionals can derive meaningful insights for decision-making processes.
Reasons for a Right-Skewed Distribution
A right-skewed distribution, as we have learned, is characterized by a longer tail on the right side of the histogram. But why does this happen? What are the reasons behind a right-skewed distribution?
One possible reason for a right-skewed distribution is the presence of outliers. Outliers are data points that deviate significantly from the rest of the dataset. These extreme values can pull the mean towards them, causing it to be higher than the median and resulting in a longer tail on the right side.
Another reason could be inherent characteristics or constraints within the data itself. For example, income distributions often exhibit a right skew because there is an upper limit to how much one can earn, but no lower limit.
Additionally, certain natural phenomena may also lead to a right-skewed distribution. Take lifespan as an example; while most individuals live until old age, few manage to reach extremely high ages which contributes to a longer tail on the histogram’s right side.
These various factors contribute to creating a right-skewed distribution in different datasets. Understanding these reasons allows us to interpret and analyze histograms more effectively and gain valuable insights into our data.
Interpreting a Right-Skewed Histogram
When analyzing a histogram, it is crucial to understand the distribution and its characteristics. A right-skewed histogram, also known as positively skewed, tells us that the data is concentrated toward the left side of the graph with a tail extending towards the right. This skewness indicates that there are relatively few high values but several low values.
In interpreting a right-skewed histogram, we can make some observations about our data set. We can see that most of the values fall on the lower end of the scale, while fewer instances occur at higher values. This suggests that there may be certain factors or constraints limiting high outcomes in this particular context.
Additionally, it’s important to consider outliers when interpreting a right-skewed histogram. Outliers are extreme values that significantly differ from other data points. These outliers could have a substantial impact on statistical analysis and should be carefully examined to determine their significance for further investigation.
Understanding how to interpret a right-skewed histogram allows us to gain valuable insights into our data distribution. By recognizing patterns and trends within our dataset through visual representation, we can make informed decisions and draw meaningful conclusions based on statistical analysis techniques suited for such distributions
Also read: University of Edinburgh: Arts and Sports Programs and Opportunities
The Importance of Outliers in a Right-Skewed Histogram
In any data set, outliers are data points that significantly differ from the rest of the observations. When analyzing a right-skewed histogram, outliers play a crucial role in understanding the distribution.
Outliers can have a significant impact on the interpretation and significance of a right-skewed histogram. These extreme values can greatly affect summary statistics such as the mean and standard deviation, which are sensitive to outliers.
For instance, if there are high-value outliers in a dataset with a right-skewed distribution, they can pull the mean towards their direction. This means that the calculated average may not truly represent most of the data. Similarly, extreme values can also influence other measures like variance or correlation coefficients.
Identifying and properly handling outliers is important for accurate analysis and decision-making based on data. Outliers could be genuine anomalies or errors during data collection or entry processes.
By carefully examining these unusual observations within a right-skewed histogram context, we gain valuable insights into potential factors driving this skewness. Additionally, it allows us to assess whether these outlier values should be included in subsequent analyses or treated separately due to their uniqueness.
Depending on domain knowledge and specific research objectives, analysts employ different strategies for dealing with outliers – ranging from removing them entirely to transforming them using statistical techniques.
Understanding how outliers affect a right-skewed histogram helps researchers avoid misleading conclusions by taking appropriate actions while interpreting results accurately.