geometry and trigonometry Notes

In the chapter you should be familiar with:

• Finding distances and midpoints
• Determining intersections of lines in a plane
• Pythagorean theorem
• Measurements in three dimensions
• Radian measure
• Trigonometric functions
• Using Pythagorean identity
• Graphical Analysis of trigonometric functions
• Voronoi diagrams

COORDINATE GEOMETRY IN A PLANE

DISTANCE AND MIDPOINT

Given the cartesian coordinates A(x₁ , y₁) and B(x₂ , y₂) the distance between A and B is given by:
AB = √(𝒙₂ − 𝒙_𝟏)^𝟐 + (𝒚₂ − 𝒚_𝟏)^𝟐

And the midpoint C(x,y) is given by ((𝒙₂ − 𝒙_𝟏)/𝟐,(𝒚₂ − 𝒚_𝟏)/2)

Example: Find the distance and midpoint between (-1, 1) and (3, 4)

Solution: Using the formula, AB = √(𝒙₂ − 𝒙_𝟏)^𝟐 + (𝒚₂ − 𝒚_𝟏)^𝟐 =√(3 – (-1)² + (4-1)² =   5

Midpoint = (𝒙₂ − 𝒙_𝟏)/𝟐,(𝒚₂ − 𝒚_𝟏)/2 = (2-(-1))/2 , (4-1)/2 = (2, 3/2)

LINES AND INTERSECTIONS

Given two lines in a plane three possibilities exist:

• Same Line: Also known as coincident lines. Two lines or shapes that lie exactly on top of each other.
• Parallel Lines: Two linesare parallel if they have the same slope, or if they are both vertical.
• Intersecting Lines: Intersecting lines are two lines that share exactly one point. This shared point is called the point of intersection.

Example: a) y = 2x-3 and y = -2x+3 are intersecting lines as their gradients are different.
b) y = 2x-3 and 2y = 2x-6 are coincident as they are the same line.
c) 2x – 6y = 4 and x – 3y = 8 are parallel as their gradient is same but intercept is different.

PERPENDICULAR LINES

If two lines are perpendicular to each other, one is said to be normal to the other at the point of intersection.
Two lines l₁ and l₂ with gradients m₁ and m₂ are perpendicular to each other if m₁m₂ = -1 and one gradient is the reciprocal of the other gradient.

Example: What line is perpendicular to x + 3y = 6 and travels through point (1,5)?
Solution: Convert the equation to slope intercept form to get y = –1/3x + 2.  The old slope is –1/3 and the new slope is 3.  Perpendicular slopes must be opposite reciprocals of each other:  m1×m2 = –1

With the new slope, use the slope intercept form and the point to calculate the intercept: y = mx + b or 5 = 3(1) + b, so b = 2 = y = 3x + 2

TRIGONOMETRY

As we have already seen in the first chapter that
“Opposite” is opposite to the angle θ
“Adjacent” is adjacent (next to) to the angle θ
“Hypotenuse” is the long one   

Sin𝜃 = 𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
Cos𝜃 = 𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
Tan𝜃 = 𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒/𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡

We define three more functions, 

Cosec𝜃 = 𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒/𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒 = 1/Sin𝜃
Sec𝜃 = 𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒/𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡 = 1/Cos𝜃
Cot𝜃 = 𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡/𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒 = 1/Tan𝜃

Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides:

Hypotenuse² = Perpendicular² + Base² → c² = a² + b²  

Angle of elevation, Angle of depression and areas of triangle including sine rule and cosine rule have been covered in chapter 1.

To recall,
𝑆𝑖𝑛𝐴/𝑎 = 𝑆𝑖𝑛𝐵/𝑏 = 𝑆𝑖𝑛𝐶/𝑐 (sine rule)
c² = a² + b² – 2abcosC (cosine rule) 
which can also be written as:
a² = b² + c² – 2bccosA

Example 1:In triangle ABC, angle of B = 21, angle of C = 46 and AB = 9cm. Solve this triangle.

Solution:We are given two angles and one side and so the sine rule can be used. Furthermore, since the angles in any triangle must add up to 180◦ then angle A must be 113◦. We know that c = AB = 9. Using the sine rule,

a/sin 113◦ = b/sin 21◦ = 9/sin 46◦

So, b/sin 21◦ = 9/sin 46◦

b = sin 21◦ × 9 sin 46◦ = 4.484cm and a = sin 113◦ × 9 sin 46◦ = 11.517cm.

Example 2: In triangle ABC, AB = 42cm, BC = 37cm and AC = 26cm. Solve this triangle.

Solution: We are given three sides of the triangle and so the cosine rule can be used. Writing a = 37, b = 26     and c = 42 we have,
a² = b² + c² − 2bc cosA
from which 37² = 26² + 42² − 2(26)(42) cosA
cos A = 26² + 42² – 37² / (2)(26)(42) = 1071/2184 = 0.4904
A = cos^-1(0.4904) = 60.63◦

You should apply the same technique to verify that B = 37.76◦ and C = 81.61◦. You should also check that the angles you obtain add up to 180◦.

DISTANCES IN THREE DIMENSIONS

Given the cartesian coordinates A(x₁ , y₁, z₁) and B(x₂ , y₂, z₂) the distance between A and B is given by:

AB = √(𝒙_𝟐 − 𝒙_𝟏)^𝟐 + (𝒚_𝟐 − 𝒚_𝟏)^𝟐 + (𝒛_𝟐 − 𝒛_𝟏)^𝟐

And the midpoint C(x,y,z) is given by ((x₂-x₁)/2 , (y₂-y₁)/2 , (z₂-z₁)/2)

Example: Find the distance and midpoint between the two points given by P(6, 4, -3) and Q(2, -8, 3).

Solution: Using distance formula to find distance between the points P and Q,
PQ = √(𝒙_𝟐 − 𝒙_𝟏)^𝟐 + (𝒚_𝟐 − 𝒚_𝟏)^𝟐 + (𝒛_𝟐 − 𝒛_𝟏)^𝟐
= √(2 − 6)^𝟐 + (-8 − 4)^𝟐 + (3 − (-3))^𝟐
= 14

Midpoint = ((x₂-x₁)/2 , (y₂-y₁)/2 , (z₂-z₁)/2) 
= ((2-6)/2 , (-8-4)/2 , (3-(-3))/2) 
= (-2, -6, 3)

ANGLES OF ROTATION AND RADIAN MEASURE

Angles of rotation are formed in the coordinate plane between the positive x-axis (initial side) and a ray (terminal side). Positive angle indicates a counter-clockwise rotation while negative angle indicates a clockwise rotation.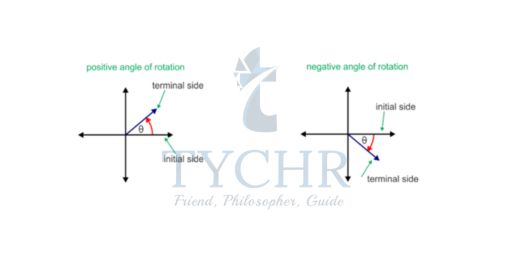

Since the x and y axes are perpendicular, each axis then represents an increment of ninety degrees of rotation. The diagrams below show a variety of angles formed by rotating a ray through the quadrants of the coordinate plane.

UNIT CIRCLE

The unit circle is the circle centred at the origin with radius equal to one unit. This means that the distance from the origin to any point on the circle is equal to one unit.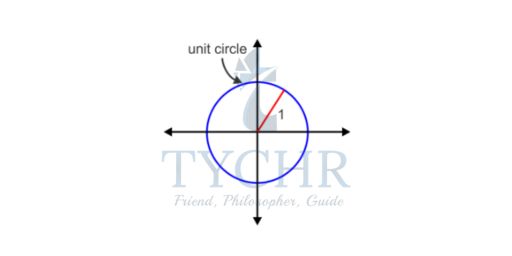Using the unit circle, we can define another unit for measurement of angles, radians. Radian measure is based upon the circumference of the unit circle. The circumference of the unit circle is 2π (2πr, where r=1). So, a full revolution, or 360∘, is equal to 2π radians. Half a rotation, or 180∘ is equal to π radians.

One radian is equal to the measure of θ, the rotation required for the arc length intercepted by the angle to be equal to the radius of the circle. In other words, the arc length is 1 unit for θ=1 radian.

We can use the equality, π=180∘ to convert from degrees to radians and vice versa.

radians × (180/π) = degrees and degrees × π/180 = radians

Example 1: a) Convert 250∘ to radians.
b) Convert 3π to degrees.

Solution: a) To convert from degrees to radians, multiply by π/180.
So, 250π/180 = 25π/18.
b) To convert from radians to degrees, multiply by 180/π. So, 3π×180/π = 3×180 = 540∘.

Example 2: Find two angles, one positive and one negative, coterminal to 5π3 and find its reference angle, in radians.

Solution: Since we are working in radians now we will add/subtract multiple of 2π instead of 360∘. Before we can add, we must get a common denominator of 3 as shown below.

5π/3+2π = 5π/3 + 6π/3 = 11π/3
and 5π/3 − 2π = 5π/3 − 6π/3 = −π/3

Now, to find the reference angle, first determine in which quadrant 5π/3 lies. If we think of the measures of the angles on the axes in terms of π and more specifically, in terms of π/3, this task becomes a little easier.

Consider π is equal to 3π/3 and 2π is equal to 6π/3 as shown in the diagram. Now we can see that the terminal side of 5π3 lies in the fourth quadrant and thus the reference angle will be:
6π/3 − 5π/3 = π/3

THE UNIT CIRCLE AND TRIGONOMETRIC FUNCTIONS

Before that we must know these terms,

1. Period: An interval containing values that occur repeatedly in a function.
2. Even function: A continuous set of (x, f(x)) points in which f(−x) = f(x), with symmetry about the y-axis.
3. Odd function: A continuous set of (x, f(x)) points in which f(−x) = −f(x), with symmetry about the origin.
4. Periodic function: A continuous set of (x, f(x)) points that repeats at regular intervals.

Sin(θ) is equal to the y-coordinate of your point, and Cos(θ) is equal to the x-coordinate.
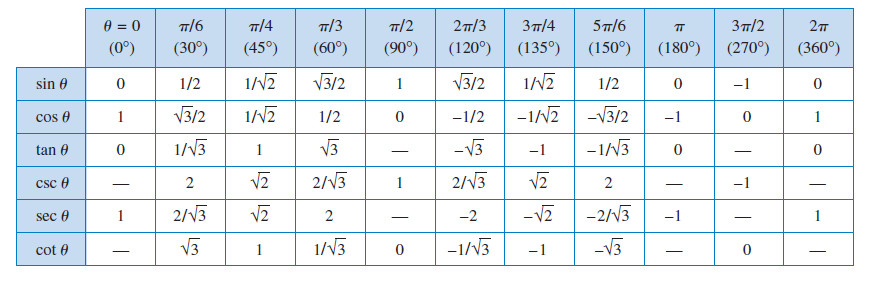
By using this concept we come up with the following table,

TRIGONOMETRIC IDENTITIES

As we know for a unit circle, x² + y² = 1, by substituting x = cosθ and y = sinθ
we get, sin²θ+ cos²θ= 1
Similarly, 1 + tan²θ= sec²θ
and 1 + cot²θ= csc²θ

Example: For a right angle triangle ABC, right angle at C for which angle BAC = θ and sinθ = 4/5. Find the value of cosθ.
Solution: Using the identity, sin²θ + cos²θ = 1
Putting value of sin in the identity,
(4/5)² + cos²θ  =1
cosθ = √1 − (4/5)² = 3/5

GRAPHICAL ANALYSIS OF TRIGONOMETRIC FUNCTIONS

This angle measure can either be given in degrees or radians. Here, we will use radians. Since any angle with a measure greater than 2π radians or less than 0 is equivalent to some angle with measure 0≤θ<2π, all the trigonometric functions are periodic.

The domain of the function y = sin(x) is all real numbers and the range is −1 ≤ y ≤ 1

The domain of the function y = cos(x) is all real numbers and the range is −1 ≤ y ≤1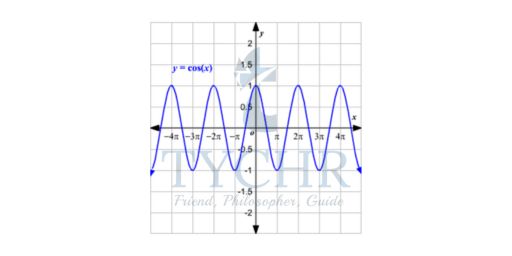

The domain of the function y = tan(x) is all real numbers except the values where cos(x) is equal to 0, i.e., the values π/2+πn for all integers n. The range of the tangent function is all real numbers.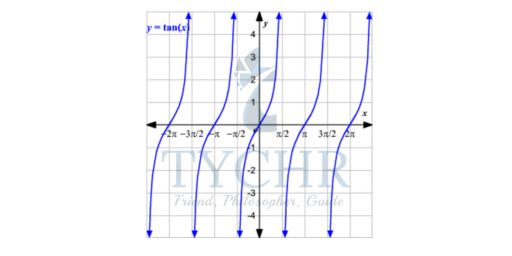

Example: Solve the equation sin2x = cosx on the interval 0 ≤ x < π

Solution: We use GDC for help, we set out x-axis to [0,π] and use the zoom fit function to get an appropriate viewing window. We enter one equation on the right hand side and another on left hand side and get the following graph:

We can see the intersections of these functions on the given interval:

So, we have three solutions: x ∈ {0.524, 1.57, 2.62}

VORONOI DIAGRAMS

Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane.

CONSTRUCTING VORONOI DIAGRAMS

Step 1: Identify your nearest neighbour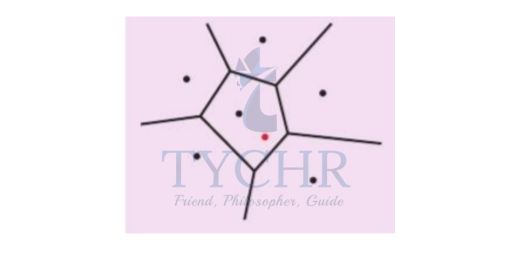

Step 2: Construct a perpendicular bisector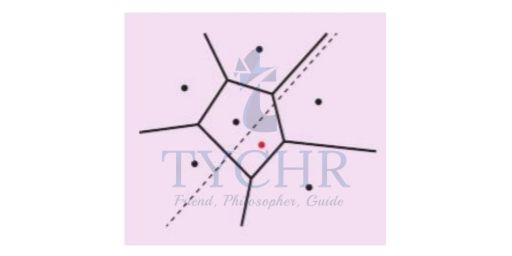

Step 3: Create a line segment with endpoints on existing cell boundaries (in red). This is the first   edge of the new cell.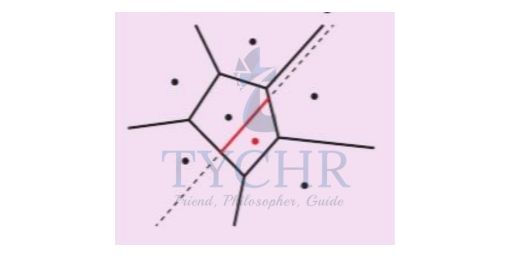

Step 4: Repeat all the steps from the start for an adjacent cell and repeat until there are no adjacent cells.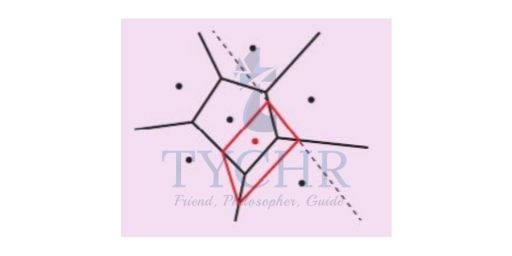

Step 5: Remove any edges inside the new cell.

Example: Create a Voronoi diagram for the points A(2,0), B(6,6), C(6,0) and D(15,3).

Solution: Begin by plotting the points and choosing two points to being with.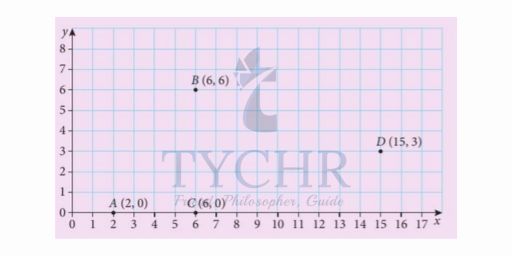

We will choose points A and B and draw a perpendicular bisector.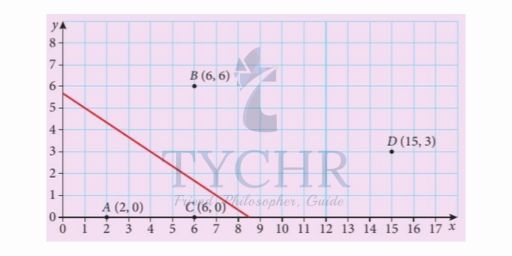

We’ll chose the next point C and do the same.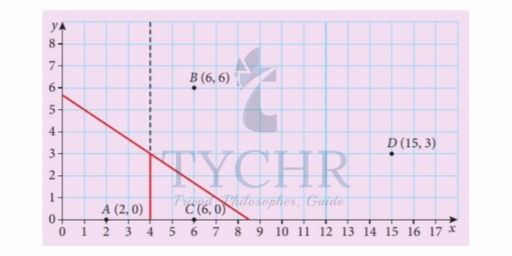

We do the same and get.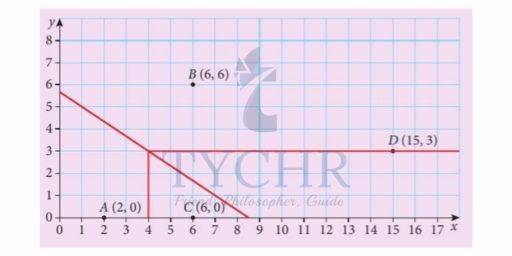

Removes edges inside the new cell.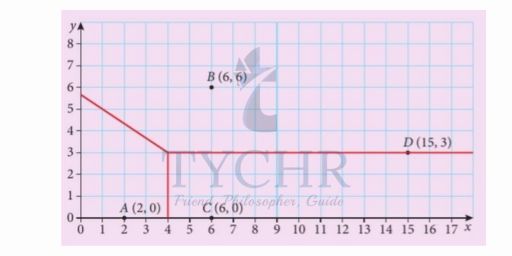

Now we add D follow the same steps as we did for C and get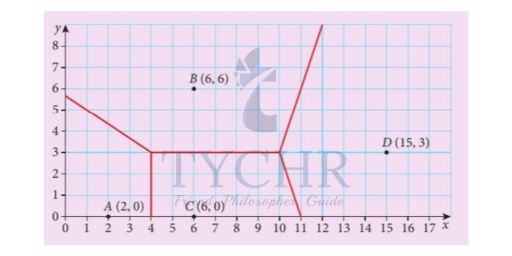

This is the final Voronoi diagram.

LARGEST EMPTY CIRCLE

To find the largest empty circle, we first locate all potential centres for that circle, which involves identifying all Voronoi vertices and finding all intersections between Voronoi edges and convex hull edges.

This problem is sometimes referred to as the Toxic Waste Dump problem, because given the coordinates for a set of cities, the LEC problem would allow you to find the best site for a toxic waste dump by finding the location which is maximally far from every city.

Example: Let’s consider the last Voronoi diagram that we got and find the coordinates of the centre and the radius of the largest empty circle.

Solution: Since, the centre of LEC must be on the vertex of the Voronoi diagram, we only have to consider two points: (4,3) and (10,3).

For (4,3), it is equidistant to sites A, B and C, so we can choose any of those coordinates to find the radius. Using site (2,0), we have:

d = √(4 − 2)² + (3 − 0)² = √13

For (10,3), it is equidistant to sites B, C and D, so we can choose any of those coordinates to find the radius. Using site (6,0), we have:

dd = √(10 − 6)² + (3 − 0)² = 5

Since 5 > , the point (10,3) must be the centre of LEC with a radius = 5.