DERIVATIVES OF EXPONENTIAL AND LOGARITHMIC FUNCTIONS

Derivative of exponential function y=e^x
The slope of the graph of y=𝑒^𝑥 exactly equals the height at every point along the curve.

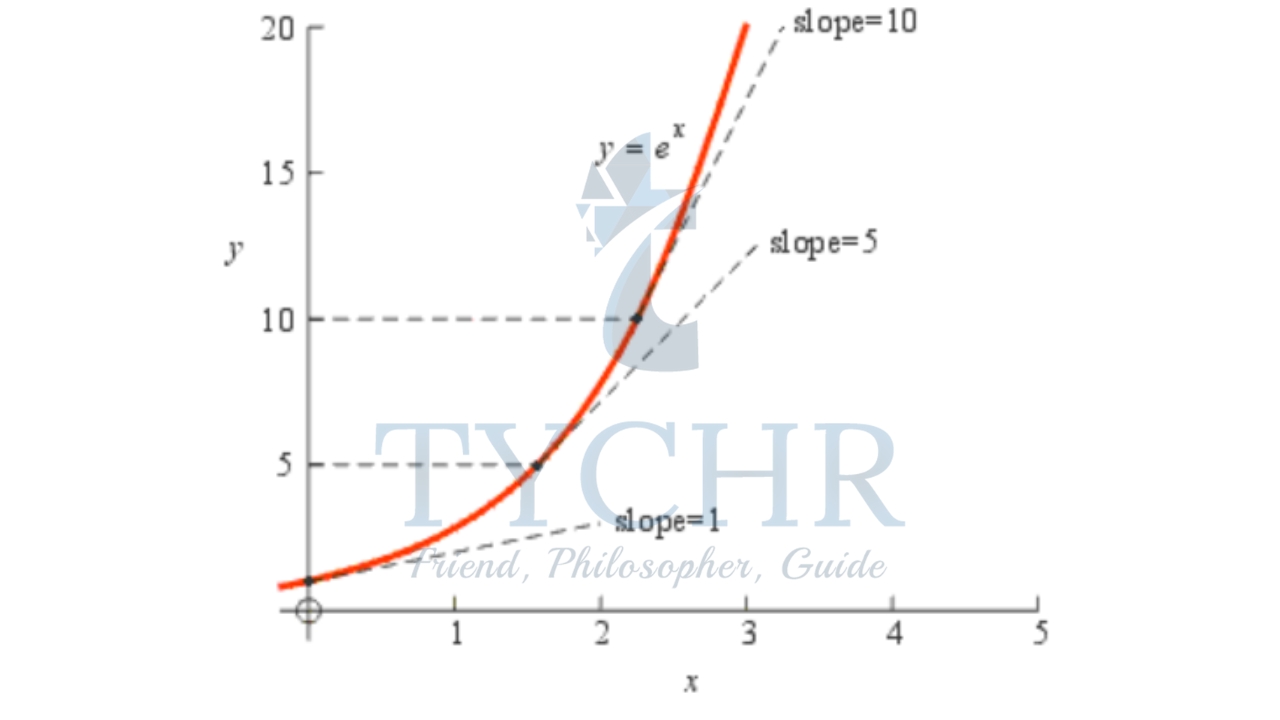
Hence, the derivative/gradient/slope of this function, equals the function itself. 𝒅(𝒆^𝒙 )/𝒅𝒙 = 𝒆^𝒙

Derivative of natural logarithm function y = lnx

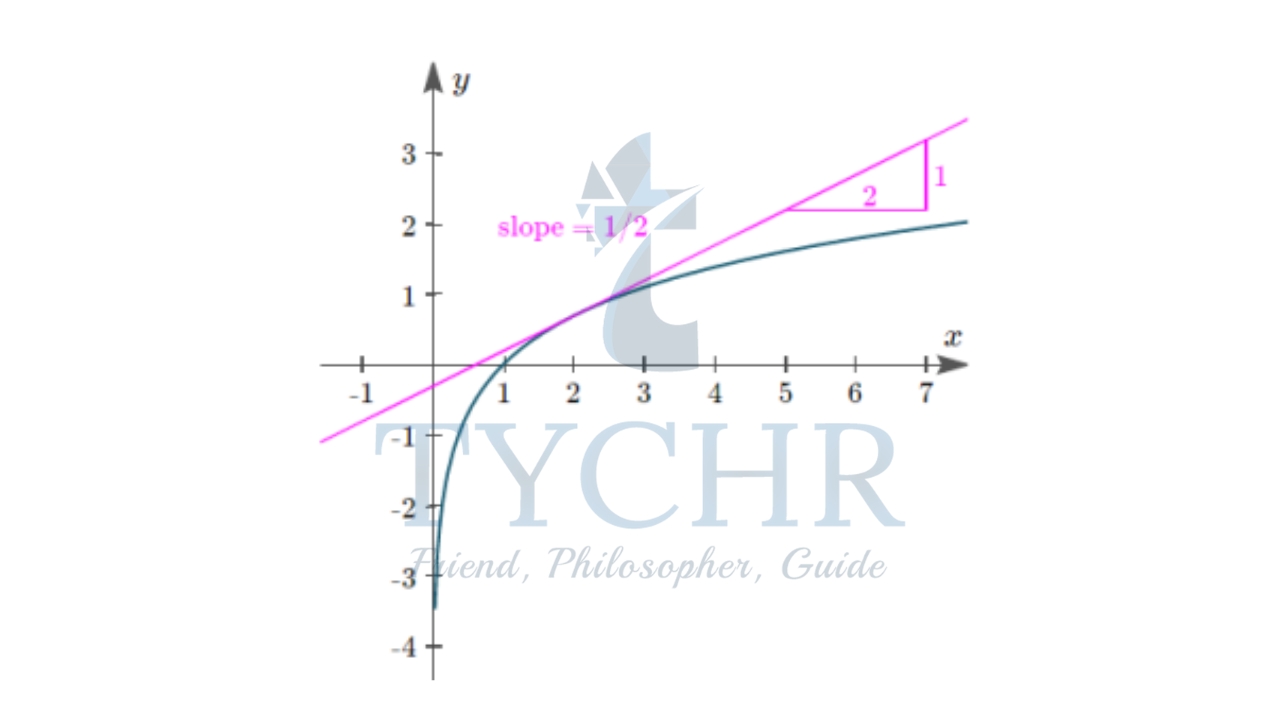
The slope of the tangent of y=ln x at x=2 is ½ . (We can observe this from the graph, by looking at the ratio rise/run)
If y=ln x

We see that the slope of the graph for each value of x is equal to 1/x.  (for all x>0)
If we did more iterations, we can conclude that derivative of logarithm function y=ln x is: d(lnx)/dx = 1/x

Ex. Find the derivative of the following:

1. y=7-2𝑒^𝑥
2. y=2𝑒^𝑥-3lnx
3. y=𝑒^𝑥–cos x

Solution:

1. 𝑦′ = 𝑑(7 − 2𝑒^𝑥)/𝑑𝑥
   𝑦′ = 𝑑(7)/𝑑𝑥 + 𝑑(−2𝑒^𝑥)/𝑑𝑥 
   𝑦′ = 0 − 2 𝑑(𝑒^𝑥)/𝑑𝑥 
   𝒚′ = −𝟐𝒆^𝒙
2. 𝑦′ = 𝑑(2𝑒^𝑥 − 3 ln𝑥)/𝑑𝑥 
   𝑦′ = 𝑑(2𝑒^𝑥)/𝑑𝑥 + 𝑑(−3 ln𝑥)/𝑑𝑥 
   𝑦′ = 2 𝑑(𝑒^𝑥)/𝑑𝑥 − 3 𝑑(ln 𝑥)/𝑑𝑥 
   𝑦′ = 2𝑒^𝑥− 3/𝑥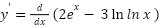
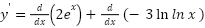
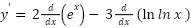
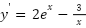
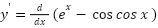
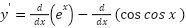
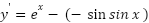
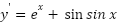
3. 
4. 

THE CHAIN RULE

The chain rule tells us how to find the derivative of a composite function.

Suppose we have two functions, f(x) and g(x):

1. f(x)=f o g(x) then the derivative of F(x) is,
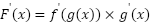
2. y=f(u) and u=g(x) then the derivative of y is, 𝒅𝒚/𝒅𝒙 = (𝒅𝒚/𝒅𝒖) × (𝒅𝒖/𝒅𝒙)

Ex. Find the derivative of the following:

1. y=cos (x²)
2. 𝑦 = √5𝑥² − 3𝑥
3. y = 1/(x²+2x)
4. y=ln (3-2x)

Solution: 1. y=cos (x²)
u=x²
𝑑𝑦/𝑑𝑢 = − sin(𝑥² )
𝑑𝑢/𝑑𝑥 = 2𝑥

𝑦′ = 𝑑𝑦/𝑑𝑥 = 𝑑𝑦/𝑑𝑢 × 𝑑𝑢/𝑑𝑥
𝑦′ = − sin(𝑥² ) × 2𝑥
𝑦 ′ = −2𝑥 sin(𝑥² )  

Shortcut :

𝑦 ′ = (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑜𝑢𝑡𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛) × (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒)
𝑦 = − sin(𝑥² ) × 2𝑥

2. 𝑦 = √5𝑥²−3𝑥
𝑢 = 5𝑥² − 3𝑥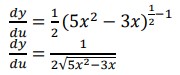𝑑𝑢/𝑑𝑥 = 10𝑥 − 3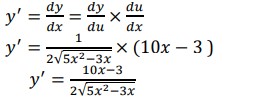

Shortcut:

𝑦′ = (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑜𝑢𝑡𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛) × (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒)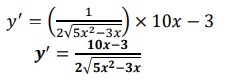c. 𝑦 = 1/𝑥²+2𝑥
𝑢 = 𝑥² + 2𝑥
𝑑𝑦/𝑑𝑢 = −1(𝑥² + 2𝑥 )⁻²
𝑑𝑦/𝑑𝑢 = − 1 (𝑥²+2𝑥 )/2
𝑑𝑢/𝑑𝑥 = 𝑑 (𝑥 2 + 2𝑥)/𝑑𝑥
𝑑𝑢/𝑑𝑥 = 2𝑥 + 2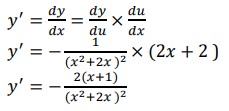
Shortcut:

𝑦 ′ = (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑜𝑢𝑡𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛) × (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒)
𝑦 ′ = (− 1/(𝑥 2+2𝑥 )²) × (2𝑥 + 2)
𝒚 ′ = − 𝟐(𝒙+𝟏)/(𝒙 𝟐+𝟐𝒙 )^𝟐 

d. y=ln (3-2x)
u=3-2x
𝑑𝑦/𝑑𝑢 = 1 3−2𝑥
𝑑𝑢/𝑑𝑥 = 0 − 2 = −2
𝑦 ′ = 𝑑𝑦/𝑑𝑥 = 𝑑𝑦/𝑑𝑢 × 𝑑𝑢/𝑑𝑥
𝑦 ′ = 1/(3−2𝑥) × (−2)
𝑦′ = − 2/(3−2𝑥)

Shortcut:
𝑦′ = (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑜𝑢𝑡𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛) × (𝑑𝑒𝑟𝑖𝑣𝑎𝑡𝑖𝑣𝑒 𝑜𝑓 𝑖𝑛𝑛𝑒𝑟 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛 𝑤𝑖𝑡ℎ 𝑟𝑒𝑠𝑝𝑒𝑐𝑡 𝑡𝑜 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒)
𝑦 ′ = 1/(3−2𝑥) × (−2)
𝒚 ′ = − 𝟐/(𝟑−𝟐𝒙)

THE PRODUCT AND QUOTIENT RULE

1. Product rule: 𝑦 = 𝑓(𝑥) × 𝑔(𝑥)
   𝒚 ′ = (𝒇(𝒙)𝒈(𝒙)) ′ = 𝒇(𝒙)𝒈 ′ (𝒙) + 𝒈(𝒙)𝒇 ′ (𝒙)
2. Quotient rule: 𝑦 = 𝑓(𝑥)/𝑔(𝑥)
   𝒚′ = ( 𝒇(𝒙)/𝒈(𝒙) ) ′ = 𝒈(𝒙)𝒇 ′ (𝒙)−𝒇(𝒙)𝒈 ′(𝒙)/ (𝒈(𝒙))^𝟐

Ex. Find the derivative of the following:

1. y=(2x+1)sin x
2. y=(1-3x²)e^x
3. y=xln x
4. 𝑦 = 𝑥−2/𝑥²+1
5. y = sinx/x

Solution:
a.) y=(2x+1)sin x
f(x)=2x+1 
g(x)=sin x  
f'(x)=2 
g'(x)=cos x  

Applying product rule:
y‘=f(x)g'(x)+g(x)f‘(x) 
y‘=2x+1cos x +2sin x  

b.) y=(1-3x²)e^x
f(x)=1-x²
g(x)=e^x
f'(x)=-6x 
g'(x)=e^x 

Applying product rule:

y‘=f(x)g'(x)+g(x)f‘(x) 
y‘=(1-3x²)e^x-6xe^x
y‘=e^x(1-3x²-6x) 

c.) y=xlnx
f(x)=x 
g(x)=ln x  
f'(x)=1 
g'(x)=1x 

Applying product rule:

y‘=f(x)g'(x)+g(x)f‘(x)
y’= x(1/x) + lnx
y‘=1+ln x  

d.) y = (x-2)/(x²+1)
f(x)=x-2
g(x)=x2+1 
f'(x)=1 
g'(x)=2x 

Applying quotient rule: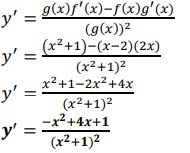

e.) y = sinx/x
f(x)=sin x
g(x)=x 
f'(x)=cos x  
g'(x)=1 

Applying quotient rule:𝑦′ = 𝑔(𝑥)𝑓′(𝑥)−𝑓(𝑥)𝑔′(𝑥)/(𝑔(𝑥))²
𝒚 ′ = 𝒙 𝐜𝐨𝐬 𝒙−𝐬𝐢𝐧 𝒙/𝒙^𝟐

KINEMATICS

Kinematics is the study of movement of objects.

• Displacement is defined to be the change in position of an object.
• Velocity is the rate of change of displacement, therefore to obtain velocity from displacement you differentiate.
• Acceleration is the rate of change of velocity. To obtain acceleration from velocity you differentiate.

Consider the following diagram:

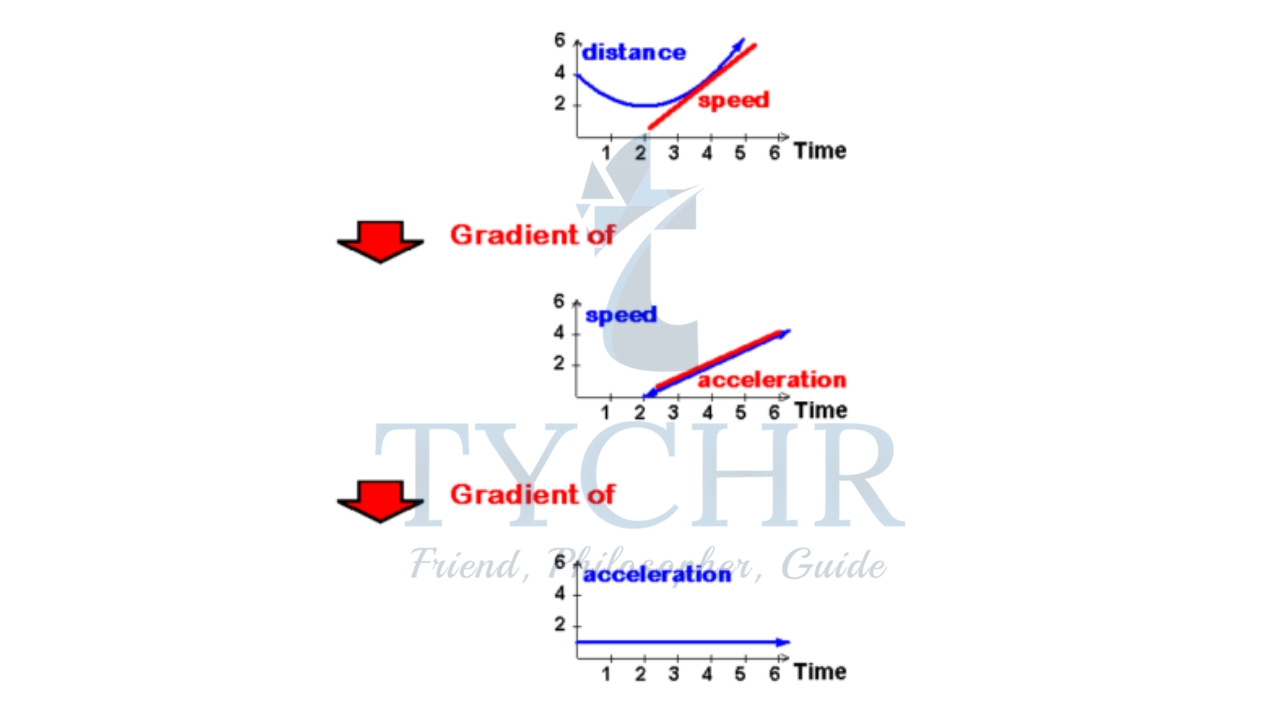
Note that if s(t) is the displacement:

• Velocity 𝑣(𝑡) = 𝑑(𝑠)/𝑑𝑡
• Acceleration a(𝑡) = 𝑑(v)/𝑑𝑡 = 𝑣(𝑡) = 𝑑²(𝑠)/𝑑²𝑡

Ex. A particle moves along a straight line such that its position at any time t is given by s(t)=5t²–t⁴. Find expressions for the velocity and acceleration of the particle in terms of t. Find the times at which:

1. the particle is at rest
2. the particle is speeding up
3. the particle is slowing down.

Solution: Given that s(t)=5t²-t⁴
𝑣(𝑡) = 𝑑(𝑠)/𝑑𝑡
𝑣(𝑡) = 𝑑(5𝑡² − 𝑡 ⁴ )/𝑑𝑡
𝑣(𝑡) = 5(2𝑡) − 4𝑡 ³
𝒗(𝒕) = 𝟏𝟎𝒕 − 𝟒𝒕 ³
at=10-12t² 

The particle will be at rest when v(t)=0
10t-4t³=0 
2t⁵-2t²=0 
t=0,  t = √5/2

The particle will be at rest at t=0 and t = √5/2
at=10-12t² 
Acceleration will change sign when at=0
10-12t²=0 
t = √5/2

Comparing the signs of velocity and acceleration:

The particle is speeding up when 0 < t < √5/6  and t > √5/2

The particle is slowing down when √5/6 < t < √5/2

OPTIMIZATION

• One common application of calculus is calculating the minimum or maximum value of a function.
• For example, companies often want to minimize production costs or maximize revenue. In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume.
• In this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter.
• We have a particular quantity that we are interested in maximizing or minimizing. However, we also have some auxiliary condition that needs to be satisfied.

Ex. The owner of a dog park has 120 feet of fencing, and wants to create a rectangular area that is divided into three rectangular pens, as in the picture below.

Find the dimensions of the rectangle that would yield the largest possible total area of the three pens. What is this area?
x=the width of pen
y= the side of each of smaller rectangular pens.
3y= length of total pen.

Total fencing needed=6y+4x=120
This can also be written as y = (120-4x)/6   ①

The total area =x(3y)
A = 3x((120-4x)/6) (From ①)
A=60x-2x²  

The maximum area will be when the derivative of area will be zero: 𝐴′ = 𝑑(60𝑥 − 2𝑥2 )/𝑑𝑥
A‘=60-4x=0 
4x=60 
x=15 Feet

Putting the value of x in ①
y = ((120 – 4(15))/6
y=10 Feet

The dimensions of the rectangle are x=15 Feet and 3y=30 Feet

Area =A=x(3y)
A=15(30) 
A=450 Square feet.

Ex.  A manufacturer needs to make a cylindrical can that will hold 1.5 litres of liquid. Determine the dimensions of the can that will minimize the amount of material used in its construction.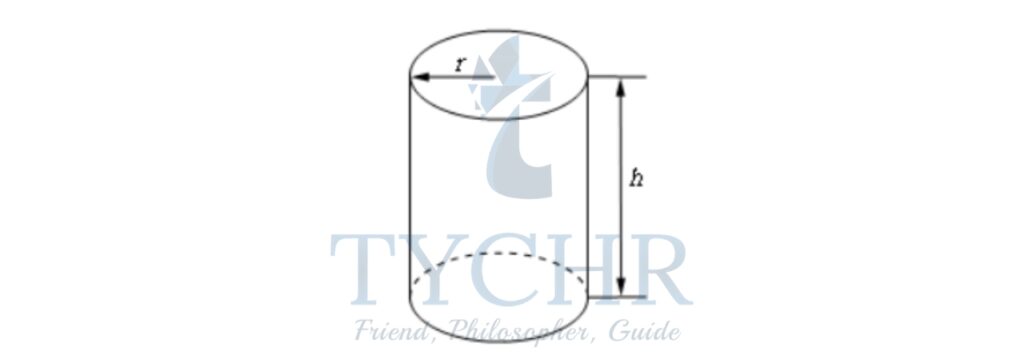

We know that, for a cylinder:
Area =A=2πrh+2πr²
Volume V=πr²h

The volume here is fixed. V=1.5 litres or V=1500cm³
1500=πr²h
h = 1500/πr²

Putting the value of h in area:
A = 2πr(1500/πr²) + 2πr²
a = 3000/r + 2πr²

Differentiating the area and equating to zero, to minimize it.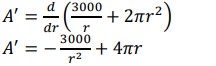Now, A’=0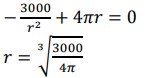r = 6.2035

We only have a single critical point to deal with here and notice that 6.2035 is the only value for which the derivative will be zero and hence the only place that the derivative may change sign.

The absolute minimum value of the area must occur at r=6.2035

Now, ℎ = 1500/𝜋𝑟²
ℎ = 1500/𝜋(6.2035)²
Therefore, if the manufacturer makes the can with a radius of 6.2035 cm and a height of 12.4070 cm the least amount of material will be used to make the can.

Ex. An apartment complex has 250 apartments to rent. If they rent x apartments then their monthly profit, in dollars, is given by, Px=-8x²+3200x-80000

How many apartments should they rent in order to maximize their profit?
Px=-8x²+3200x-80000 

To maximize this profit, we will differentiate and equate it to zero. We need to make sure the value of x is less than or equal to 250.

𝑃 ′ (𝑥) = 𝑑(−8𝑥² + 3200𝑥 − 80000)/𝑑𝑥
𝑃 ′ (𝑥) = −8(2𝑥) + 3200
𝑃 ′ (𝑥) = −16𝑥 + 3200

Now, P‘(x)=0
-16x+3200=0 
x=320016 
x=200 

Since the profit function is continuous and we have an interval with finite bounds we can find the maximum value by simply plugging in the only critical point that we have and the end points of the range.

P(0)=-80,000 
P(200)=240,000 
P(250)=220,000 

So, it looks like they will generate the most profit if they only rent out 200 of the apartments instead of all 250 of them.