Download our Successful College Application Guide
Our Guide is written by counselors from Cambridge University for colleges like MIT and other Ivy League colleges.
To join our college counseling program, call at +918825012255
IB Math AI SL Paper 1 Question Bank
The IB Math AI SL Paper 1 Question Bank is an excellent resource for students preparing for their IB Math AI SL Paper 1 examination. The question bank contains a wealth of practice questions, covering all the topics in the syllabus. The questions are of varying difficulty, so students can test themselves at their own level. The answer key included with the question bank is also very helpful, providing step-by-step explanations of how to solve each problem. Overall, the IB Math AI SL Paper 1 Question Bank is an excellent tool for students who are serious about doing well on their IB Math AI SLPaper 1 exam.
1.) The velocity of a particle moving along a straight line is given by the function v(t) = 3t2 – 4t + 2, where t is the time in seconds.
a) Find an expression for the displacement function s(t) for the particle.
To find the displacement function s(t), we need to integrate the velocity function v(t) with respect to t.
The integral of v(t) is given by the antiderivative of the function:
∫ v(t) dt = ∫ (3t2 – 4t + 2) dt
Using the power rule for integration, we integrate term by term:
∫ v(t) dt = (t3 – 2t2 + 2t) + C
Therefore, the displacement function s(t) is given by s(t) = t3 – 2t2 + 2t + C, where C is the constant of integration.
b) Find the total displacement of the particle from t = 0 to t = 4 seconds.
To find the total displacement of the particle from t = 0 to t = 4 seconds, we evaluate the definite integral of the displacement function s(t) over the interval [0, 4]:
∫[0, 4] s(t) dt = [(43 – 2(4)2 + 2(4)) – (03 – 2(0)2 + 2(0))]
Simplifying:
∫[0, 4] s(t) dt = [64 – 2(16) + 8] – [0 – 0 + 0]
∫[0, 4] s(t) dt = [64 – 32 + 8] – [0]
∫[0, 4] s(t) dt = 40
Therefore, the total displacement of the particle from t = 0 to t = 4 seconds is 40 units.
2.) The temperature (T) in a room is given by the equation T = -0.02×2 + 0.6x + 20, where x represents the number of hours since 9:00 AM.
a) Find the vertex of the quadratic equation and interpret its meaning in the context of the problem.
To find the vertex of the quadratic equation, we can use the formula x = -b / (2a), where the quadratic equation is in the form ax2 + bx + c. Comparing the given equation T = -0.02x2 + 0.6x + 20 with the standard quadratic form, we have a = -0.02 and b = 0.6.
x = -b / (2a)
x = -0.6 / (2(-0.02))
x = -0.6 / (-0.04)
x = 15
The vertex of the quadratic equation is (15, T), where T represents the temperature. In the context of the problem, it means that at 15 hours after 9:00 AM, the temperature reaches its maximum or minimum value.
b) Determine the maximum and minimum values of the temperature in the given time interval.
To determine the maximum and minimum values of the temperature, we can substitute the x-coordinate of the vertex into the equation T = -0.02x2 + 0.6x + 20.
T = -0.02(15)2 + 0.6(15) + 20
T = -4.5 + 9 + 20
T = 24.5
Therefore, the maximum value of the temperature is 24.5°C.
To find the minimum value, we can observe that the quadratic equation has a negative coefficient for the x2 term, indicating a concave-down shape. This means that the maximum value occurs at the vertex, and the minimum value occurs at one of the endpoints of the given time interval.
Since the time interval is not specified in the question, we cannot determine the exact minimum value. However, we can say that the minimum value occurs either at the starting time (9:00 AM) or at the ending time (end of the specified time interval).
c) After how many hours does the temperature reach its minimum value?
Without the time interval specified, we cannot determine exactly when the temperature reaches its minimum value. However, we can say that the time at which the minimum value occurs is either at the starting time (9:00 AM) or at the ending time (end of the specified time interval).
3.) Consider the quadratic -4x2 +120x-800
a)
i) Find the roots.
To find the roots of the quadratic equation -4x2 + 120x – 800 = 0, we can use the quadratic formula:
x = (-b ± √(b2 – 4ac)) / (2a)
In this case, a = -4, b = 120, and c = -800. Substituting these values into the quadratic formula, we get:
x = (-120 ± √(1202 – 4(-4)(-800))) / (2(-4))
x = (-120 ± √(14400 – 12800)) / (-8)
x = (-120 ± √1600) / (-8)
x = (-120 ± 40) / (-8)
So the roots of the quadratic equation are:
x1 = (-120 + 40) / (-8) = -10
x2 = (-120 – 40) / (-8) = 20
ii) Hence express the quadratic in the form y= a(x-x1)(x-x2)
y= -4(x-10)(x-20)
b)
i) Find the coordinates of the vertex.
To find the coordinates of the vertex, we can use the formula x = -b / (2a), where a = -4 and b = 120:
x = -120 / (2(-4))
x = -120 / (-8)
x = 15
To find the corresponding y-coordinate, substitute x = 15 into the quadratic equation:
y = -4(15)2 + 120(15) – 800
y = -900 + 1800 – 800
y = 100
So the coordinates of the vertex are (15, 100).
ii) Hence express the quadratic in the form y= a(x-h)2 +k
Expressing the quadratic in the vertex form y = a(x – h)2 + k, we substitute the values of h and k:
y= -4(x-15)2 +100
iii) Write down the equation of the axis of symmetry
The equation of the axis of symmetry is given by x = h. Therefore, the equation of the axis of symmetry in this case is x = 15.
iv) Write down the maximum value of y
The maximum value of y occurs at the vertex, so the maximum value of y is 100.
c) Write down the y- intercept of the quadratic
To find the y-intercept, substitute x = 0 into the quadratic equation:
y = -4(0)2 + 120(0) – 800
y = -800
Therefore, the y-intercept of the quadratic is -800.
4.) Solve the equation: (ln x)2 – lnx2 +1 = 0
To solve the equation (ln x)2 – ln(x2) + 1 = 0, we can use substitution to simplify it. Let’s substitute y = ln x:
(y)2 – ln(e2y) + 1 = 0
Simplifying further:
y2 – 2y + 1 = 0
Now we have a quadratic equation in terms of y. We can solve this quadratic equation by factoring:
(y – 1)2 = 0
Taking the square root of both sides:
y – 1 = 0
y = 1
Now we substitute back y = ln x:
ln x = 1
To solve for x, we exponentiate both sides using the property of logarithms:
elnx = e1
x = e
Therefore, the solution to the equation (ln x)2 – ln(x2) + 1 = 0 is x = e.
5.) Solve the equation 2sin2x = sin x for 0≤ x ≤ 2π
To solve the equation 2sin2(x) = sin(x) for the interval 0 ≤ x ≤ 2π, we can rewrite it as a quadratic equation by moving all terms to one side:
2sin2(x) – sin(x) = 0
Now, let’s factor out sin(x) from the equation:
sin(x)(2sin(x) – 1) = 0
To find the solutions, we set each factor equal to zero and solve separately:
sin(x) = 0
The solutions to this equation occur when sin(x) is equal to zero. In the given interval, this happens at
x = 0 and x = π.
Next, consider the factor 2sin(x) – 1:
2sin(x) – 1 = 0
Solving this equation, we isolate sin(x):
2sin(x) = 1
sin(x) = 1/2
The solution to this equation is x = π/6 and x = 5π/6 in the given interval.
Therefore, the solutions to the original equation 2sin2(x) = sin(x) for 0 ≤ x ≤ 2π are:
x = 0, x = π/6, x = π, x = 5π/6.
6.) Let f(x) = 2x2 – 12x +10. Find the tangent and normal line at x = 2.
To find the tangent and normal line to the function f(x) = 2x2 – 12x + 10 at x = 2, we need to find the slope of the tangent line and the slope of the normal line at that point.
First, we find the derivative of the function f(x):
f'(x) = 4x – 12
Next, we evaluate the derivative at x = 2 to find the slope of the tangent line:
f'(2) = 4(2) – 12 = -4
So the slope of the tangent line at x = 2 is -4.
Now we need to find the equation of the tangent line. We know that the tangent line passes through the point (2, f(2)) = (2, 2(2)2 – 12(2) + 10) = (-6). Therefore, we can use the point-slope form of a line:
y – (-6) = -4(x – 2)
Simplifying this equation, we get:
y = -4x + 2
So the equation of the tangent line to the function f(x) at x = 2 is y = -4x + 2.
To find the slope of the normal line, we know that the product of the slopes of perpendicular lines is -1. Therefore, the slope of the normal line at x = 2 is the negative reciprocal of the slope of the tangent line:
m = -1/(-4) = 1/4
Now we need to find the equation of the normal line. Using the point-slope form of a line and the point (2, -6), we get:
y – (-6) = (1/4)(x – 2)
Simplifying this equation, we get:
y = (1/4)x – 5/2
So the equation of the normal line to the function f(x) at x = 2 is y = (1/4)x – 5/2.
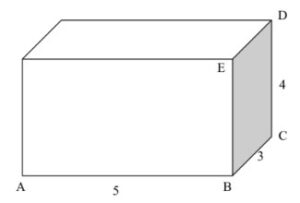
7.) Consider the following cuboid of dimensions 5*3*4, as shown.
a) Find the length AC.
AC2= 52+32
AC = √34
b) Find the length AD.
AD2 = √342+42 = √50
c) Find the angle of elevation from A to E.
tanEAB = 4/5
EAB = 38.7°
d) Find the angle of elevation from A to D.
tanDAC = 4/√34
DAC= 34.4°
8.) The population of a city is given by the equation P(t) = 2000e(0.02t), where t represents the number of years since the year 2000.
a) Find the population in the year 2025.
To find the population in the year 2025, we need to substitute t = 25 into the equation P(t):
P(25) = 2000e(0.02(25))
P(25) = 2000e(0.5)
P(25) ≈ 2000 * 1.648721
P(25) ≈ 3297.44
Therefore, the population in the year 2025 is approximately 3,297.
b) Determine the average annual growth rate of the population over the interval from 2000 to 2025.
The average annual growth rate can be determined by finding the slope of the function P(t) = 2000e(0.02t) over the interval from 2000 to 2025. We can calculate it by finding the change in population divided by the change in time:
Average growth rate = (P(25) – P(0)) / (25 – 0)
= (3297.44 – 2000) / 25
= 1297.44 / 25
≈ 51.8976
Therefore, the average annual growth rate of the population over the interval from 2000 to 2025 is approximately 51.8976.
c) Estimate the year in which the population will reach 10,000.
To estimate the year in which the population will reach 10,000, we need to solve the equation
P(t) = 10,000:
10,000 = 2000e(0.02t)
Dividing both sides by 2000:
5 = e(0.02t)
Taking the natural logarithm (ln) of both sides:
ln(5) = 0.02t
Simplifying:
t = ln(5) / 0.02
Using a calculator, we find:
t ≈ 69.3157
Therefore, the year in which the population will reach 10,000 is estimated to be approximately 2069.
9.) The heights of students in a school are normally distributed with a mean of 165 cm and a standard deviation of 7 cm. When students’ heights are classified, they are categorized as tall if their height is greater than 180 cm.
a) Determine the probability that a randomly selected student will be classified as tall.
To determine the probability that a randomly selected student will be classified as tall, we need to find the probability of a height greater than 180 cm.
Using the normal distribution, we can standardize the height value using the formula z = (x – mean) / standard deviation.
For x = 180 cm, the standardized value is:
z = (180 – 165) / 7
z = 15 / 7 ≈ 2.14
Using a standard normal distribution table or a calculator, we can find the corresponding probability. The probability of a height greater than 180 cm is approximately 1 – 0.983 or 0.017.
Therefore, the probability that a randomly selected student will be classified as tall is approximately 0.017 or 1.7%.
Approximately 95% of the students have heights within the average height category, which is between k cm and 173 cm.
b) Find the value of k.
To find the value of k, we need to determine the height value that corresponds to the lower end of the average height category.
Using the normal distribution, we can standardize the height value for x = k cm:
z = (k – 165) / 7
To find the corresponding z-value for 95% of the students, we refer to the standard normal distribution table. The z-value that corresponds to an area of 0.95 is approximately 1.645.
Setting the standardized value equal to 1.645 and solving for k:
1.645 = (k – 165) / 7
Multiplying both sides by 7:
11.515 = k – 165
Adding 165 to both sides:
k ≈ 176.515
Therefore, the value of k is approximately 176.515 cm.
10.) The random variable X is normally distributed with μ= 100. It given that P(X > 130) = 0.2 Write down the values of the following probabilities
a) P(X < 130)
P(X < 130) = 0.8
b) P(X < 70)
P(X < 70) = 0.2
c) P(100<X < 130)
 P(100<X < 130) = 0.3
d) P(70<X < 130)
P(70<X < 130) = 0.6
e) P(X > 70)
To find P(X > 70), we can use the complement rule for probabilities: P(X > 70) = 1 – P(X < 70).
Since we have already calculated P(X < 70) to be 0.2 in part (b), we can substitute this value into the formula:
P(X > 70) = 1 – P(X < 70) = 1 – 0.2 = 0.8.
f) P(X = 100)
Since X is a continuous random variable and follows a normal distribution, the probability of X taking a specific value, such as 100, is infinitesimally small. In other words, P(X = 100) is approximately equal to 0 in a continuous normal distribution.
g) P(X > 100)
To find P(X > 100), we can use the cumulative distribution function (CDF) of the normal distribution. For a normal distribution with mean μ and standard deviation σ, the CDF is denoted as Φ(x), where x is the value of the random variable.
Given that X is normally distributed with mean μ = 100, we need to know the standard deviation σ in order to calculate the CDF Φ(x) and find P(X > 100). If the standard deviation σ is known, we can use statistical tables or a calculator with a normal distribution function to find the value of Φ(x) at x = 100 and subtract it from 1 to get P(X > 100).
11.) For the event A and B, P(A) = 0.6, P(B) = 0.8 and P(A∪B) = 1
a) Find P(A∩B)
P(A∩B)= 0.6 + 0.8 – 1 = 0.4
b) Find P(A’∪ B’)
P(A’∪ B’) = 0.6
c) Find P(A’∩B)
To find P(A’∩B), we can use the formula for conditional probability: P(A’∩B) = P(A’∣B) * P(B), where P(A’∣B) is the conditional probability of A’ given B.
Since P(A) = 0.6 and P(A∪B) = 1, we can deduce that P(A’∪B) = 1 – P(A∪B) = 1 – 1 = 0.
Now, we can use the formula for conditional probability to find P(A’∣B):
P(A’∣B) = 1 – P(A∣B), where P(A∣B) is the conditional probability of A given B.
Since P(A) = 0.6 and P(B) = 0.8, we can deduce that P(A∣B) = P(A∪B) – P(B) = 1 – 0.8 = 0.2.
Therefore, P(A’∩B) = P(A’∣B) * P(B) = (1 – P(A∣B)) * P(B) = (1 – 0.2) * 0.8 = 0.64.
d) Find P(A’∪B)
To find P(A’∪B), we can use the formula for the union of events: P(A’∪B) = P(A’) + P(B) – P(A’∩B).
Since we have already found P(A’∩B) to be 0.64 in part (c), we can substitute this value into the formula:
P(A’∪B) = P(A’) + P(B) – P(A’∩B) = 1 – P(A) + P(B) – P(A’∩B) = 1 – 0.6 + 0.8 – 0.64 = 0.56.
e) Find P(A∪B’)
To find P(A∪B’), we can use the formula for the union of events: P(A∪B’) = P(A) + P(B’) – P(A∩B’).
Since P(B’) = 1 – P(B) = 1 – 0.8 = 0.2, we can substitute the given probabilities into the formula:
P(A∪B’) = P(A) + P(B’) – P(A∩B’) = 0.6 + 0.2 – P(A∩B’).
However, we do not have the value of P(A∩B’) given in the question, so we cannot determine the exact value of P(A∪B’) without additional information.
f) Find P(B|A)
To find P(B|A), we can use the formula for conditional probability: P(B|A) = P(A∩B) / P(A).
Since we have already found P(A∩B) to be 0.4 in part (a), and P(A) is given as 0.6 in the question, we can substitute these values into the formula:
P(B|A) = P(A∩B) / P(A) = 0.4 / 0.6 = 0.67 (rounded to two decimal places).
12.) The value of a car, C, depreciates exponentially over time. The formula for the value of the car, in thousands of dollars, is given by:
C = 50(0.9)t
where t is the time in years since the car was purchased.
a) Find the initial value of the car when it was purchased.
(a) To find the initial value of the car, we need to substitute t = 0 into the formula:
C = 50(0.9)t
C = 50(0.9)0
C = 50(1)
C = 50
Therefore, the initial value of the car when it was purchased was $50,000.
b) If the car is 4 years old, what is its current value?
(b) To find the current value of the car, we need to substitute t = 4 into the formula:
C = 50(0.9)t
C = 50(0.9)4
C = 50(0.6561)
C = 32.805
Therefore, the current value of the car is $32,805.
c) What is the rate of depreciation of the car in dollars per year?
The rate of depreciation of the car is the change in value over time, or the derivative of the formula:
C = 50(0.9)t
dC/dt = 50(ln 0.9)(0.9)t
At t = 0 (when the car was purchased), we have:
dC/dt = 50(ln 0.9)(0.9)0
dC/dt = 50(ln 0.9)(1)
dC/dt = -5.77
Therefore, the rate of depreciation of the car is $5,770 per year.
13.) Astronomers classify the brightness of stars according to a scale of magnitudes. The difference in magnitude between two stars is defined by the formula
m_1 – m_2 = 2.5 log (L_2 / L_1)
where m_1 and m_2 are the magnitudes of the two stars, and L_1 and L_2 are the corresponding luminosities measured in watts. The magnitude of a star is a unitless measure, and its value can be positive or negative.
a) The star Proxima Centauri has a magnitude of 11.05. The star Alpha Centauri has a magnitude of -0.27. Calculate the ratio of their luminosities, L_2 / L_1.Â
We can rearrange the formula to solve for the ratio of luminosities:
m_1 – m_2 = 2.5 log (L_2 / L_1)
L_2 / L_1 = 10((m_1 – m_2) / 2.5)
Substituting m_1 = 11.05 and m_2 = -0.27, we get:
L_2 / L_1 = 10((11.05 – (-0.27)) / 2.5)
L_2 / L_1 = 10(11.32 / 2.5)
L_2 / L_1 = 31593.25
Therefore, the ratio of luminosities of Proxima Centauri to Alpha Centauri is 31593.25.
b) The star Betelgeuse has a magnitude of 0.45 and a luminosity of 100,000 L_sun, where L_sun is the luminosity of the Sun. Calculate the apparent magnitude of Betelgeuse as seen from Earth.
We can rearrange the formula to solve for the apparent magnitude:
m_1 – m_2 = 2.5 log (L_2 / L_1)
m_1 = m_2 + 2.5 log (L_2 / L_1)
Substituting m_2 = -26.7 and L_2 = 100000 L_sun, and using the fact that the luminosity of the Sun is L_sun = 3.828 × 1026 W, we get:
m_1 = -26.7 + 2.5 log (100000 L_sun / L_sun)
m_1 = -26.7 + 2.5 log (100000)
m_1 = -26.7 + 12.5
m_1 = -14.2
Therefore, the apparent magnitude of Betelgeuse as seen from Earth is -14.2.
Our Expert Tutors!
Amrita
IBDP Maths AIhl
ap statistics
Aiman
IBDP Biology
ap Biology
Jyoti
IBDP Business Management
ap microeconomics
Vaishnavi Thakur
IBDP ESS
Ap Environmental Science
SOURAV
IBDP Physics
ap physics c mechanics
Get access to our free IB resources
IBDP Study Notes
IB Comprehensive Syllabus
IB IA Ideas
IB CAS Ideas
