IB Physics HL Paper 2 Question Bank
Check Out Our Results

OXFORD UNIVERSITY
(QS:3)

IMPERIAL COLLEGE
(QS:6)

CORNELL UNIVERSITY (QS:16)

45/45 (IBDP)
GEORGIA INSTITUTE

43/45 (IBDP)
KELLY SCHOOL
The IB Physics HL Paper 2 Question Bank is a great resource for students preparing for the IB Physics HL exam. The questions are well-written and cover a broad range of topics, making it a valuable tool for studying. The question bank is also updated regularly, so students can be sure they’re getting the most current information.
Time: 2 hours and 15 minutes
Instructions to candidates
- Answer all questions.
- Answers must be written within the answer boxes provided.
- A calculator is required for this paper.
- A clean copy of the physics data booklet is required for this paper.
- The maximum mark for this examination paper is [90 marks].
Answer all questions. Answers must be written within the answer spaces provided.
1.) The air in a kitchen has a pressure of 1.20 x 105 Pa and a temperature of 23 C. There is a refrigerator inside the kitchen with an internal volume of 0.38 m3.
a.) When the refrigerator door is open, the temperature and pressure of the air inside the kitchen and inside the refrigerator are the same. Calculate the number of air molecules in the refrigerator.
Answer
PV = nRT
N = PV / RT
N = (1.20 x 105 x 0.38) / ((273 + 23 ) x 8.314 = 18.529 = 18.5 mol
Number of molecules = 18.5 x 6.023 x 1023 = 1.1 x 1025
b.) When the refrigerator door is closed, the temperature inside cools down to 4 C with the same amount of air molecules.
i.) Determine the pressure of the air inside the refrigerator round to 3 significant figures
Answer
P1T1 = P2T2
1.2 x 105 x (273+23) = P2 x (273+4)
P2 = (1.20 x 105 x (273+23)) / (273+4)
P2 = 128231.0469 → (1.28 x 105 Pa)
ii.) The area of the door of the refrigerator is 0.75 m2. Determine the minimum force needed to open the refrigerator door.
Answer
Force = Difference in pressure x Area
Force = (128231 – 120000) x 0.75 = 6173.25 = 6.17 kN
2.) The diagram below shows a sketch of a step down transformer with a voltage of 200 Volts. The number of turns in the primary coil is 1600 and 80 in the secondary coil.
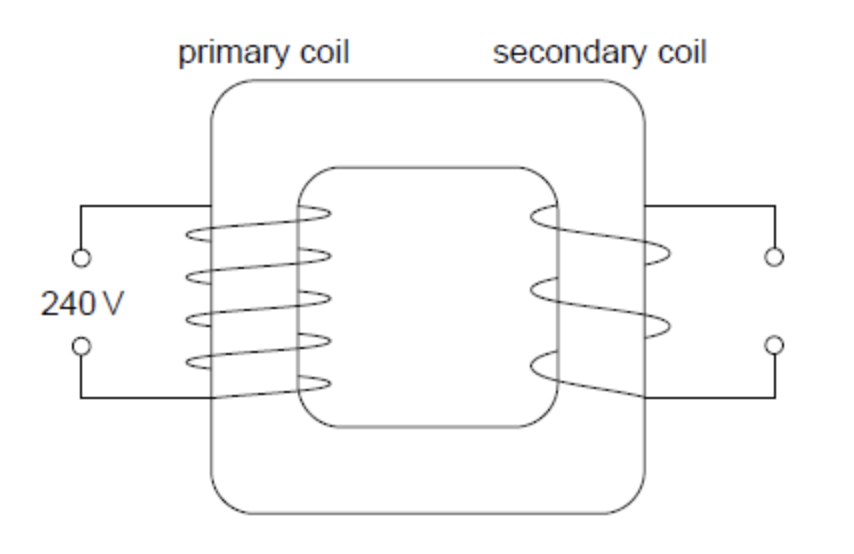
a.) State Faraday’s Law of Induction
Answer
The induced emf is equal to the number of loops multiplied by the change in flux over a period of time
b.)
i.) Explain the working of the step down transformer using Faraday’s Law of Induction
Answer
The varying current or voltage in the primary coil induces a varying magnetic field. This in turn produces a change in the flux (change in the magnetic field) of the secondary coil. Due to this, a varying magnetic field is induced in the secondary coil as well. Given that there are more turns in the primary coil than the secondary coil, the voltage is stepped down.
ii.) Calculate the output voltage with a known input voltage of 200 V
Answer
output voltage = (number of turns in the secondary coil x input voltage) / (number of turns in the primary coil) = (80×200)/1600=10 V
c.) Outline how energy losses occur in the core of a transformer
Answer
When the core of the transformer is laminated, it tends to reduce the eddy currents. This in turn reduces the thermal energy that is transferred to the surroundings.
3.) An electron is placed 0.50 m from a fixed point charge of -5.8 mC.
a.) Determine the electric field strength due to the point charge at the position of the electron
Answer
E = kq / r2
E = (8.99 x 109 x 5.8 x 10-3) / 0.52
E = 208568000 = 2.09 x 108 N/C
b.) Calculate the force acting on the electron
Answer
F = qE
F = 1.6 x 10-19 x 2.09 x 108 = 3.344×10−11 N
4.) An electron follows a circular motion in a uniform magnetic field. The velocity of the electron at a Point P is 7.2 x 105 m/s towards the right direction. The magnitude of the magnetic field is 8.1T.
a.) State the direction of the magnetic field
Answer
Out of the page according to the Right hand rule. The index finger is pointed towards the direction in which the electron is moving. The thumb points down and the middle finger points outwards indicating that it’s out of the page.
b.) Calculate the magnitude of the magnetic force acting on the electron in terms of N.
Answer
F = qvB
F = 1.6 x 10-19 x 7.2 x 105 x 8.1
F = 9.3312×10−13 → 9.3 ×10−13 N
c.) State why the electron moves
i.) at a constant speed
Answer
The magnetic force does not act on the electron or does not do any work on the electron. Because of this, it does not change the kinetic energy of the electron. The kinetic energy remains constant only if the speed is constant.
ii.) along a circular path
Answer
The velocity of the electron is at a right angle to the magnetic field. Since the magnetic force is acting towards the center of the circle, there is a centripetal force acting on the charge
5.) The ball is displaced at a distance of x from the bottom center of the bowl and is released from a stationary position.
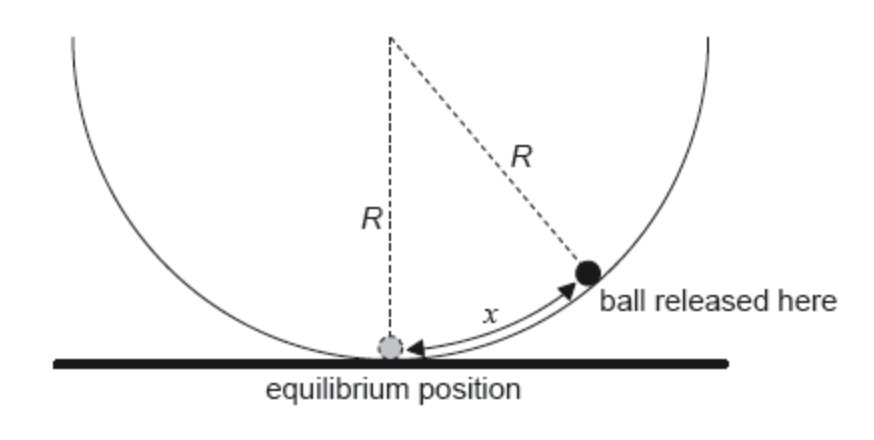
The magnitude of the force acting on the bowl is given by the following equation: mgx/R where R is the radius of the bowl which is 5.2 m.
a.)
i.) Suggest why the ball will perform simple harmonic motions about the equilibrium position
Answer
The restoring force is proportional to the displacement.
ii.) Show that the period of the oscillation is about 14 seconds
Answer
ω = √(g/R) = √ω(9.81/5.2) = 1.37 s-1 (rounding to 4 sig. figures)
Using this, we can find the time period of the oscillation with the help of this formula:
T = 2π/ω = (2×9.81)/1.374=14.28s ∼ 14 seconds
iii.) The amplitude of the oscillation is 0.16 m. On the axes given below, draw a graph to show one period of the ball Answer
Answer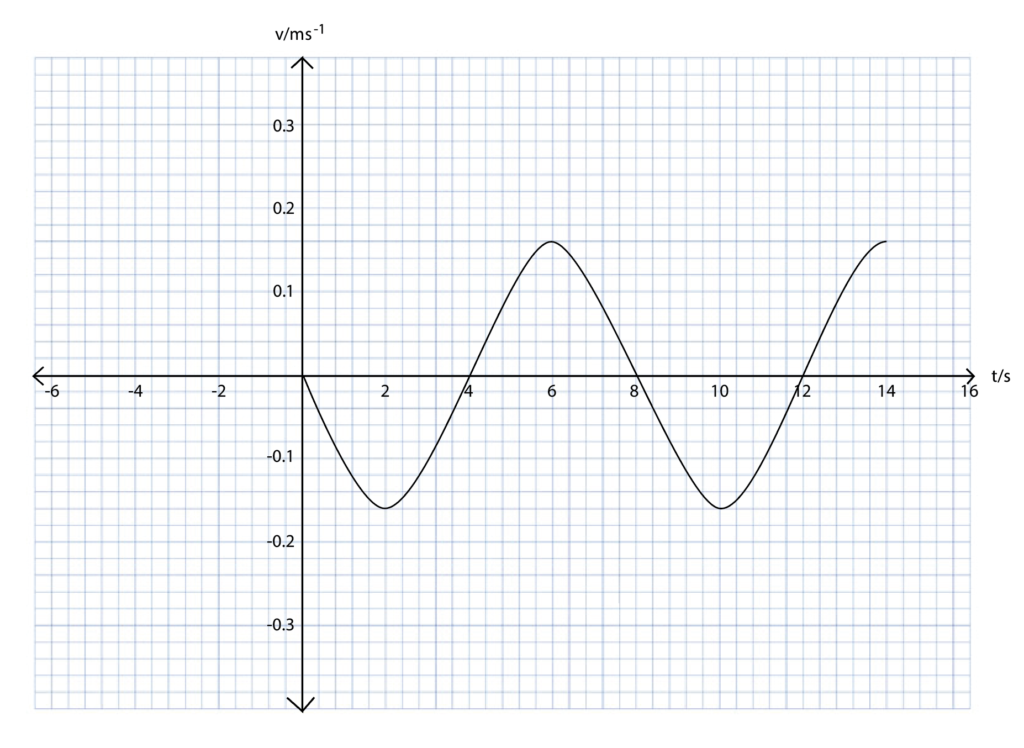
6.)
a.) State what happens to the density of a nucleus when there is a change in the number of nucleons
Answer
The density remains constant. It does not vary with the number of nucleons in the nucleus
b.) Determine the radius of a Magnesium-24’s nucleus
Answer
Radius = R0 x A1/3
Radius = 1.2 x 10-15 x 241/3
Radius = 3.46 x 10-15 m
c.) Define decay constant
Answer
The decay constant of a radioactive nuclide is its probability of decay per unit time.
7.) In a school experiment, a small electric motor is used with a capacitor of 14 mF and a battery. The capacitor is charged with the help of the battery when the switch is connected to a point X. However, when the switch is connected to Y, the capacitor fully discharges through the small electric motor and helps raise a small mass.
a.) The battery has an electromotive force (emf) of 6.8 volts. Determine how much charge flows through the motor when the mass is raised.
Answer
Charge = Capacitance x Volts
Charge = 14 x 10-3 x 6.8 = 0.0952 C
b.) The electric motor has the ability to transfer ⅔ of the electric energy stored in the capacitor into the gravitational potential energy. What is the maximum height that a 52 g mass can be raised?
Answer
Energy that is stored in the capacitor is denoted by ½ CV2
E = ½ x 14 x 10-3 x 6.82 = 0.324 J
Using that energy, the height can be found using the standard mgh formula
Therefore, Energy = mgh
Height = Energy / mg
Height = ⅔ x (0.324 / (0.052 x 9.81)) = 0.423 = 0.42 m
The height was multiplied by ⅔ because it said that the motor is only able to transfer ⅔ of the electric energy stored in the capacitor
8.) Mars has two moons orbiting around it in a circular orbit. The moon Deimos and Phobos. This question will be about the moon Deimos.
a.) State the origin of the force that acts on the moon Deimos.
Answer
Gravitational force of Mars acts on the moon Deimos to keep it orbiting around
b.) This force does not do any work on the moon Deimos. Outline why.
Answer
Since the force and the velocity are perpendicular to each other, no work is done on the moon. When they are at 90 degrees to each other, there is no change in the gravitational potential energy.
9.) A boy is riding a bicycle up a slope that is inclined by 5 degrees from the horizontal. The boy’s bicycle is powered by an electric motor and has a battery that transfers energy to the electric motor. The total weight of the boy and the bicycle is 70 kgs.
a.) Calculate the weight component of the boy and the bicycle acting down the slope.
Answer
Weight component is mass x gravitational constant x sin theta
Weight = 70g x sin(5) = 59.849 = 59.8 N
b.) When the boy goes up the slope again, he takes an additional bag with him. Outline and explain if this would change the maximum distance he can travel on his bicycle along the slope.
Answer
Since he is carrying more weight, more resistive forces will act on him. Due to this increase in the opposing force, the maximum distance he covers will reduce. It also reduces for two other reasons: if he carries more mass up a slope, more work needs to be done to cover a larger distance. Another reason is that most of the kinetic energy is now potential energy since the speed of the boy has also reduced.
c.) The boy’s bicycle has a meter on it. It displays the emf and the current for the battery when the bicycle is in motion. This is what was displayed at one such moment:
Current: 6.2 A Potential Difference: 15 V emf of the cell: 18 V
Determine the internal resistance of the battery
Answer
Resistance = potential difference / current
Resistance = (18 – 15) / 6.2 = 0.483 ohms
d.) The bicycles battery is an arrangement of 10 identical cells where 5 are connected in series and in one series circuit, two are connected in parallel. Calculate the emf one cell.
Answer
Emf of the cell / number of cells in a circuit
Emf of one cell = 18 / 5 = 3.6V
10.) Through a beta plus decay, Phosphorus – 30 can be formed from Silicon – 30.
a.) Write down the nuclear reaction that shows the beta plus decay
Answer
3015P → 3014Si + 0+1e + ve
b.) Sketch the Feynman diagram that represents the above reaction
Answer
udu quarks become udd – W+ is emitted
Electron neutrino direction is outside
Positron direction is inside
c.) Define quark confinement
Answer
A quark is an elementary particle with an electric charge. But a single quark is never found alone. Instead, when particles are smashed together and quarks are detected, they are described like ends of rubber bands that stretch, but eventually pull quarks back together again. This is known as quark confinement.


