stoichiometric relationships Notes
Stoichiometric relationships are fundamental to quantitative chemistry in the IBDP Chemistry course. A strong grasp of these relationships is essential for predicting reactant and product quantities in chemical reactions. This study note explores key stoichiometric concepts, including the mole, molar mass, Avogadro’s constant, empirical and molecular formulas, and balancing chemical equations. These concepts are crucial for both the IB Chemistry syllabus and a comprehensive understanding of chemical processes. If you need additional support in mastering these core ideas, remember that many resources are available to help you succeed.
Introduction to the particular nature of matter and chemical change.
States of matter
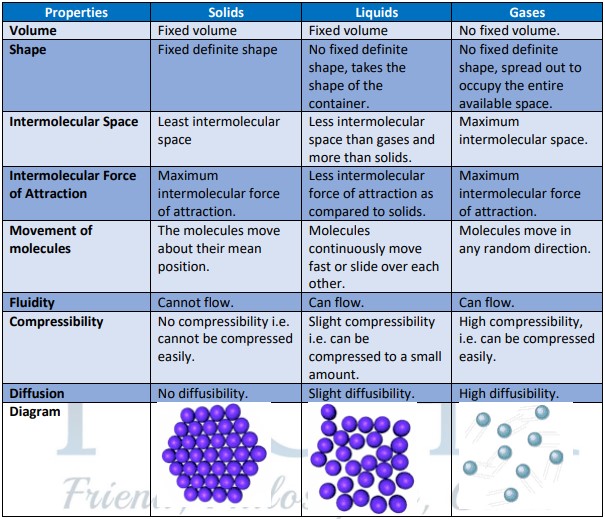
- Matter is defined as anything that has mass and takes up space (it has volume). The properties of three states of matters are summarized below:
Temperature and Kinetic Energy
- Temperature is a measure of the average kinetic energy of the particles of a substance.
- The SI unit for temperature is the Kelvin (K).
- You can convert temperatures from the Celsius scale to the Kelvin scale using the algorithm: Temperature (K) = temperature (°C) + 273.15
- Kinetic energy (KE) refers to the energy associated with movement or motion.
- State symbols are used to show the states of the reactants and products taking part in a reaction.
State | Symbol | Example |
solid | (s) | Mg(s) |
liquid | (l) | Be2(l) |
gas | (g) | N2(g) |
aqueous (dissolves in water) | (aq) | HCL(aq) |
Changes of state
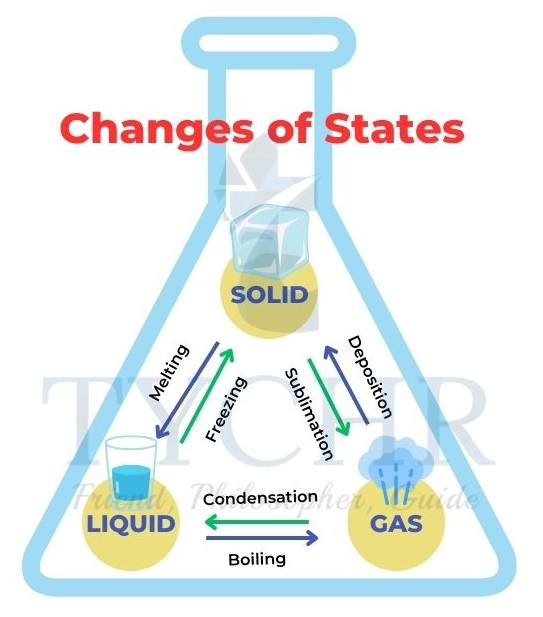
- As the movement or kinetic energy of the particles increases with temperature, they will overcome the inter-particle forces and change state.
- Sublimation: When solid turns into a gas without first becoming liquid.
- Deposition: The reverse of sublimation that changes a gas directly to solid.
- Condensation: When gaseous state changes into liquid state.
- As shown in Figure 2 the temperature increases until it reaches the melting point of water i.e. 0°C.
- There is no change in temperature while melting is occurring. All of the energy is being used to disrupt the lattice, breaking the attractive forces between the molecules and allowing the molecules to move more freely.
- The temperature rises until it reaches the boiling point of water at 100 °C (373 K), and the water starts to boil.
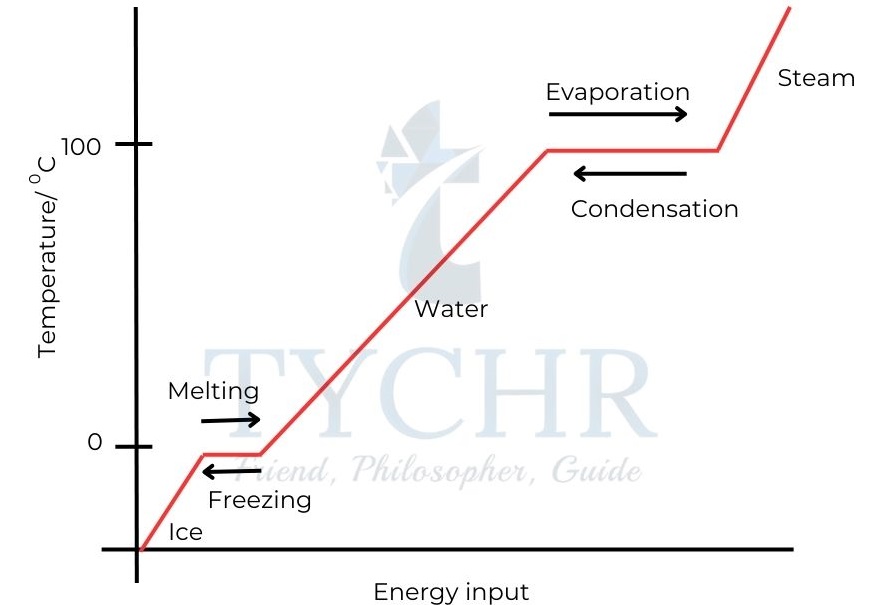
Figure 2: The heating curve of water. - Again the temperature does not change as energy is required to overcome the attractive forces between the molecules in the liquid water in order to free water molecules from the liquid to form a gas.
- Melting and boiling are endothermic processes. Energy must be transferred to the water from the surroundings to bring about these changes of state.
- Condensation and freezing are exothermic processes. Energy is transferred to the surroundings from the water during these changes of state.
Elements, Compounds and Mixtures
- Elements: Elements are substances (like hydrogen and oxygen) that can’t be split into simpler substances.
- Compounds: A substance like water that is made up of two or more elements is called a compound.
- Mixtures: A mixture is a combination of two or more distinct substances that are physically joined together without the use of any chemical bonds.

Flow Chart 1: Elements, Compounds and mixtures.
Common combinations of elements: Background to writing equation
- An ion is a charge species. Anions are negatively charged and cations are positively charged.
- Compounds contain a fixed proportion of elements, and are held together by chemical bonds.
- The formation of compounds from elements is an example of chemical change and can be represented by a chemical equation.
- The total number of atoms in each element must be the same on both sides of the equation due to the fact that atoms are neither created nor destroyed during a chemical reaction.
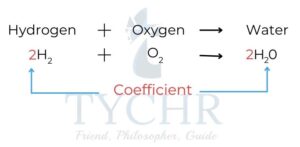
- This is known as balancing the equation, and uses numbers called stoichiometric coefficients
to denote the number of units of each term in the equation. - To balance an equation we change the coefficients of a formula not the formula itself.
- First balance the metallic element on each side of the equation– add a number in front of the symbol on one side if necessary so that there is the same number of atoms of this element on each side.
- Balance any elements that occur in only one formula on the reactant and products side. Sometimes polyatomic ions remain unchanged in reactions and they can be balanced easily at this stage.
- Balance the remaining elements if necessary.
The atom economy
- Atom economy is the efficiency of chemical reactions by comparing the molecular mass of atoms in the reactants with the molecular mass of useful compounds.
Percentage atom economy = (Molecular mass of atoms of useful products /Molecular mass of atoms in reactants)× 100% - In an ideal chemical process the amount of reactants = amounts of products produced.
- So an atom economy of 100% would suggest that no atoms are wasted.
- A higher atom economy indicates a more efficient and less wasteful process.
The mole concept
- All chemical substances are made up of elements that are composed of their constituent atoms, which vary in the number of protons, neutrons, and electrons.
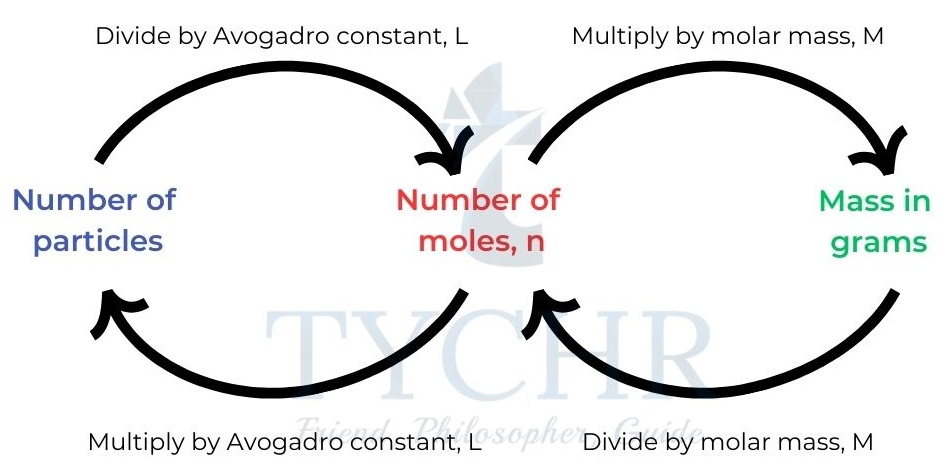
- The mole is an SI unit, symbol mol, defined as a fixed amount, n, of a substance.
- This fixed amount is a number of particles called Avogadro’s constant (symbol L or NA) and it has a value of 6.02 × 1023 mol-1
- We can calculate the number of particles in any portion or multiple of a mole of a substance.

Figure 4: Calculating number of particles or number of moles.
Relative atomic mass, relative formula mass, and molar mass
- Isotopes are atoms of the same element with different numbers of neutrons but the same number of protons in the nucleus.
- The relative atomic mass Ar of an atom is a weighted average of the atomic masses of its isotopes and their relative abundances.
- The relative molecular mass or relative formula mass Mr for a molecule or formula unit is determined by combining the Ar values of the individual atoms or ions.
- Ar and Mr have no units as they are both ratios.
- The mass of one mole of a substance is known as the molar mass.It has the unit of grams per mole, g mol-1.
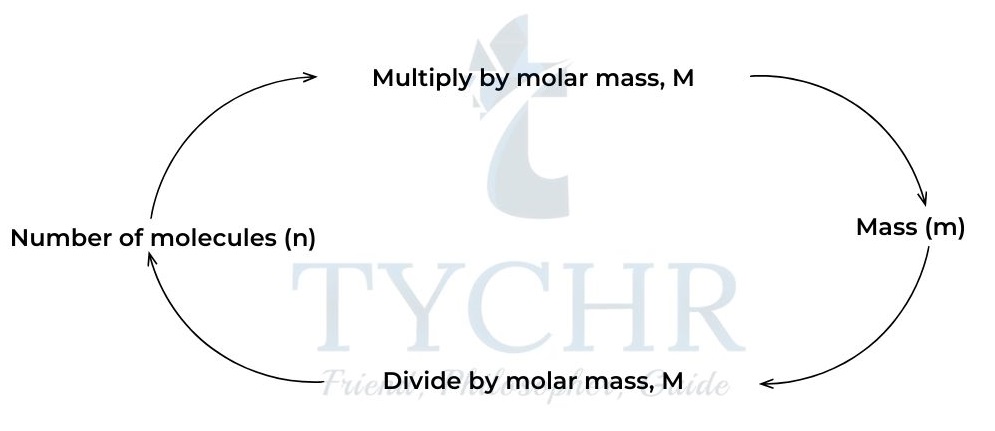
Figure 5: Calculating mass and number of moles.
Mole calculations
Experimental empirical and molecular formula determination
- The empirical formula of a compound is the simplest whole-number ratio of atoms or amount (in mol) of each element present in a compound.
- The molecular formula is the actual number of atoms or amount (in mol) of elements in one structural unit or one mole of the compound, respectively.
Substance
Molecular formula
Empirical formula
Ethane C2H6 CH3 Water H2O H2O Hydrogen peroxide H2O2 HO Butanoic acid C4H8O2 C2H4O Glucose C6H12 O6 CH2O
Reacting masses and volumes
Chemical equations show reactants combining in a fixed molar ratio
- Chemical change, as summarized in chemical equations, is simply an expression of reactants combining in fixed ratios to form products.
- The most convenient means to express this ratio is as moles, as that gives us a means of relating the number of particles that react to the mass that we can measure.
- Example:
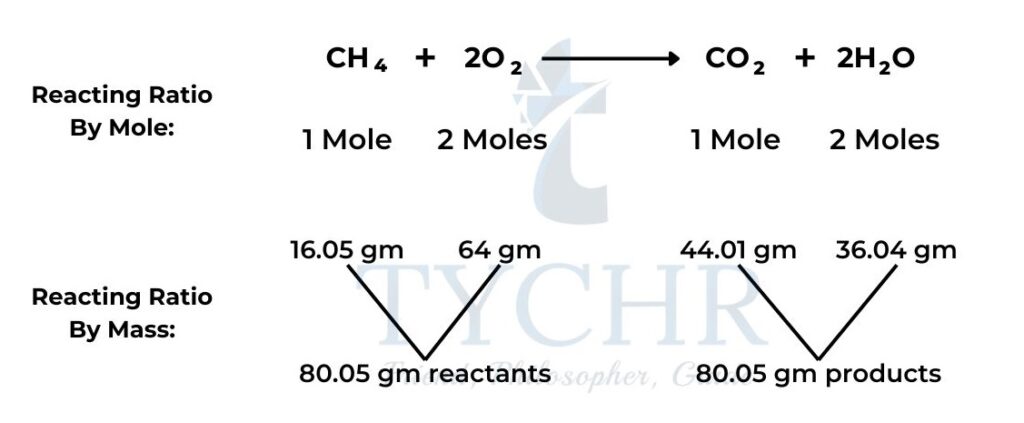
The limiting reagent
- The limiting reactant is the reactant that determines the quantity of the product.
- The limiting reagent, often the more expensive reactant, will be completely consumed during the reaction.
- Other reactants will therefore not be fully used, and are said to be in excess.
- The theoretical yield, which is usually expressed in grams or moles, refers to the maximum amount of product obtainable, assuming 100% of the limiting reactant is converted to product.
- Note that identification of the limiting reactant depends on the mole ratios in the balanced chemical equation for the reaction. This means that if reactant quantities are given in grams, they must first be converted to moles.
Theoretical and experimental yields
- The balanced chemical equation represents what is theoretically possible when a reaction is carried out under ideal conditions.
- It allows the expected amount of products to be calculated – the theoretical yield.
- To calculate the percentage yield a comparison is made between the theoretical yield and the actual amount produced in the process – the experimental yield:
Percentage yield = ( experimental yield / theoretical yield )× 100%
Avogadro’s law and the molar volume of a gas
- A model used to explain and predict the behaviour of gases at the microscopic level is the kinetic theory of gases. An important physical property of a gas is its pressure, the force exerted by a gas as its particles collide with a surface.
- Imagine taking a mass numerically equal to the molar mass of different gases and using each to inflate a balloon.
- Under the same conditions of temperature (0 °C/273 K) and pressure (100kPa) the balloons will have the same volume.
- These particular temperature and pressure conditions are known as standard temperature and pressure (STP).
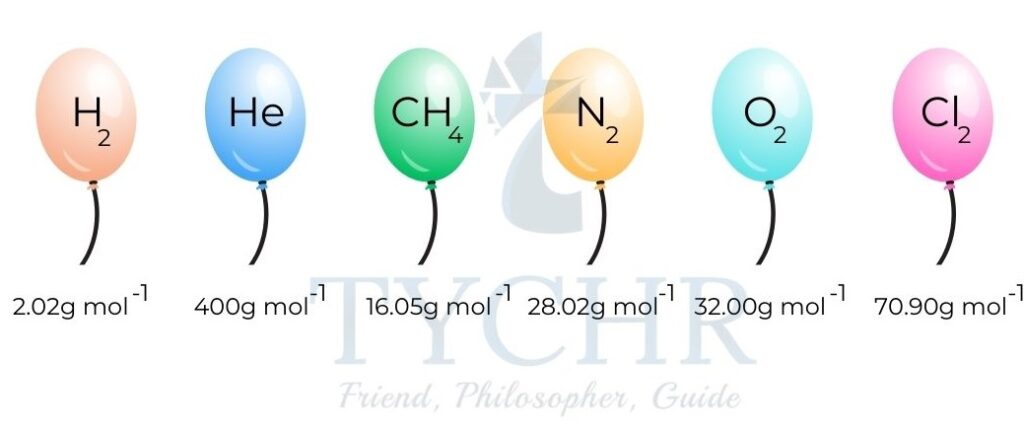
Figure 7: The molar volume of any gas is identical at a given temperature and pressure. - At STP, the balloons will have identical volumes of 22.7 dm3 mol-1. This is the molar volume of an ideal gas and it is constant at a given temperature and pressure.
- This understanding is known as Avogadro’s law, which states that: Equal volumes of all gases, when measured at the same temperature and pressure, contain an equal number of particles.
- Using V for volume and n for number of moles: V ∝ n.
The gas laws
1. Boyle’s law: Relationship between volume and pressure
- If the temperature is held constant, it is found that increasing the pressure on a fixed mass of gas decreases its volume.
- To put it another way, the ratio of a gas’s volume to its pressure is negative, and the sum of the two is constant.
P ∝(𝟏/𝑽) ; PV = a constant - This relationship is often known as Boyle’s law, as it was first established by Robert Boyle in 1662.
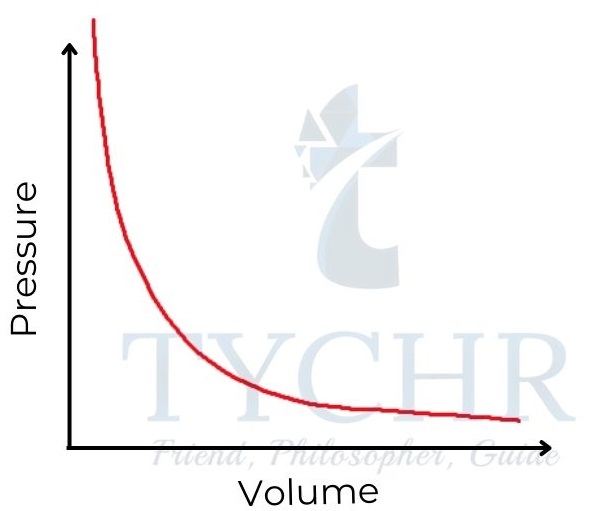
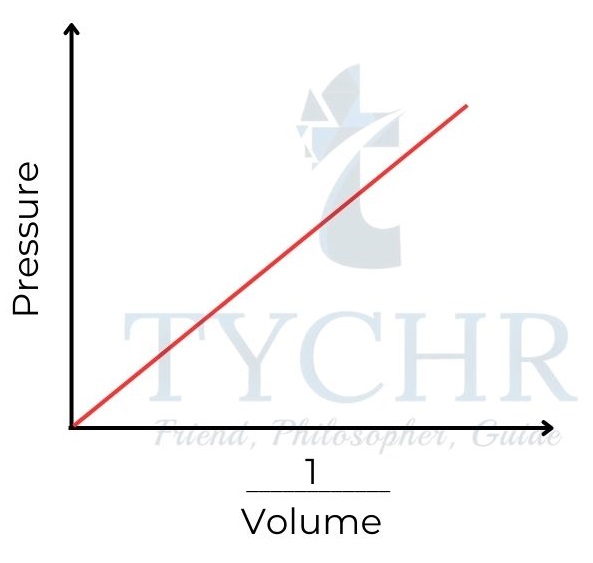
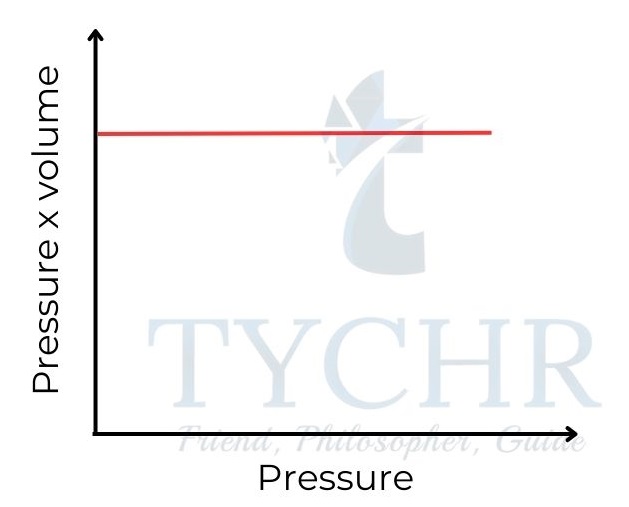
Figure 8: Boyle’s law. Gas pressure is inversely proportional to its volume.
2. Charles’s law: Relationship between volume and temperature
- If the pressure is held constant, it is found that increasing the temperature of a fixed mass of gas increases its volume.
- In other words, the volume of a gas is directly proportional to its absolute temperature, and volume divided by absolute temperature is a constant.
V ∝ T ; 𝑽/𝑻 = a constant - This relationship is often known as Charles’ law, as it was first established by Frenchman Jacques Charles in the late 18th century.
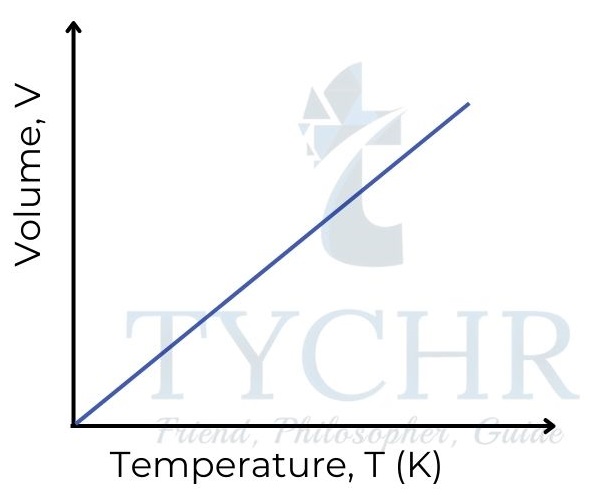
3. Gay-Lussac’s law: Relationship between pressure and temperature
- If the volume is held constant, it is found that increasing the temperature of a fixed mass of gas proportionately raises its pressure.
- In other words, the pressure of a gas is directly proportional to the absolute temperature, and pressure divided by temperature is a constant.
P ∝ T ; 𝑷/𝑻 = a constant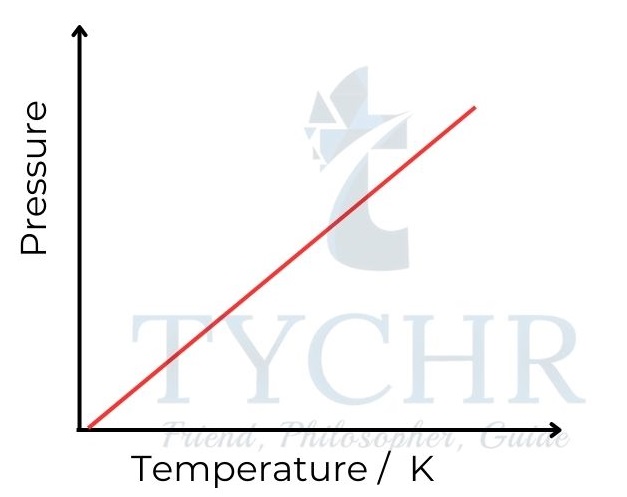
The combined gas law
- The three gas laws, Charles’s law, Boyle’s law, and Gay-Lussac’s law, are combined in one law
called the combined gas law. - For a fixed amount of gas, the relationship between temperature, pressure, and volume is:
(𝐏𝟏𝐕𝟏)/𝐓𝟏 = (𝐏𝟐 𝐕𝟐)/𝐓𝟐
The ideal gas equation
- The combined gas equation tells us that 𝑃𝑉/ T = a constant.
- The value of the constant is directly proportional to the fixed mass of gas, or the number of
moles, n. So (𝑃𝑉/𝑇)∝ n. - This can be made into an equation by introducing a constant, R, known as the universal gas constant.
PV = nRT - This equation is known as the ideal gas equation.
- This means that for one mole of gas, the relationship PV/RT should be equal to 1. So a graph of PV/RT against P for one mole of an ideal gas is a horizontal line of intercept 1

Concentration
- A homogeneous mixture of a solute that has been dissolved in a solvent is called a solution.
- The solute is usually a solid, but could be a liquid or gas. When the solvent is water the solution is described as an aqueous solution.
- We express the amount of solution through its concentration.
- The molar concentration of a solution is defined as the amount (in mol) of a substance dissolved in 1 dm3 of solvent. 1 dm3 = 1 litre (1 L).
Concentration of solution (mol dm-3) = 𝐚𝐦𝐨𝐮𝐧𝐭 𝐨𝐟 𝐬𝐨𝐥𝐮𝐭𝐞 (𝐦𝐨𝐥)/𝐯𝐨𝐥𝐮𝐦𝐞 𝐨𝐟 𝐬𝐨𝐥𝐮𝐭𝐢𝐨𝐧 (𝐝𝐦𝟑) or c = n/V - Chemists routinely prepare solutions of known concentration, known as standard solutions
- A different unit of concentration is known as ppm, parts per million. It denotes one part per 106 by mass, and is useful in describing very low concentrations such as those found in air and water pollution.
Parts per million (ppm) = (𝐦𝐚𝐬𝐬 𝐨𝐟 𝐜𝐨𝐦𝐩𝐨𝐧𝐞𝐧𝐭/𝐭𝐨𝐭𝐚𝐥 𝐦𝐚𝐬𝐬 𝐨𝐟 𝐬𝐨𝐥𝐮𝐭𝐢𝐨𝐧) × 106 - A common practice in laboratory work is to make a dilution from a more concentrated starting solution, called the stock solution, by adding solvent.
Titrations
- Quantitative analysis includes a range of laboratory techniques used to determine the amount or concentration of an analyte.
- Volumetric analysis is a quantitative technique used by chemists involving two solutions.
- A titration involves a standard solution of known concentration which is added to a solution of unknown concentration until the chemical reaction is complete.
- The reaction progress is monitored through colour changes using indicators.
Stoichiometry in IB Chemistry develops a deep understanding of quantitative chemical reactions.
Mastering these concepts, as outlined here, prepares you for advanced IBDP Chemistry topics. Consistent practice is vital. For personalized support in stoichiometry and other IB Chemistry areas, consider working with a tutor. TYCHR connects students with experienced IB Chemistry HL & SL tutors , helping you achieve your best. A solid foundation in stoichiometric relationships is crucial for success in IB DP Chemistry.

