By the end of this chapter, you will be familiar with:

• The concept of limit
• Derivative as function and as rate of change
• Derivative of different type of functions
• Relation between graph, first derivative and second derivative of a function
• Increasing and decreasing functions
• Maxima, minima and inflection points
• Finding equations of Tangent and Normal

INTRODUCTION

DIFFERENTIAL CALCULUS

• Differential calculus deals with the study of the rates at which quantities change. It is one of the two principal areas of calculus (integration being the other).
• The need of differential calculus lies in the question- What is the instantaneous rate of change of something?
• We know how to calculate the average speed of a car for the last 10 minutes, for the last minute or for the last second. But by using the fundamental formula (speed equals distance over time), we cannot calculate the speed of the car right now!
• To calculate this instantaneous rate of change of things, we use differential calculus.
• We can say, it is all about what is happening in this instant.

AVERAGE AND INSTANTANEOUS CHANGE

Consider the following diagram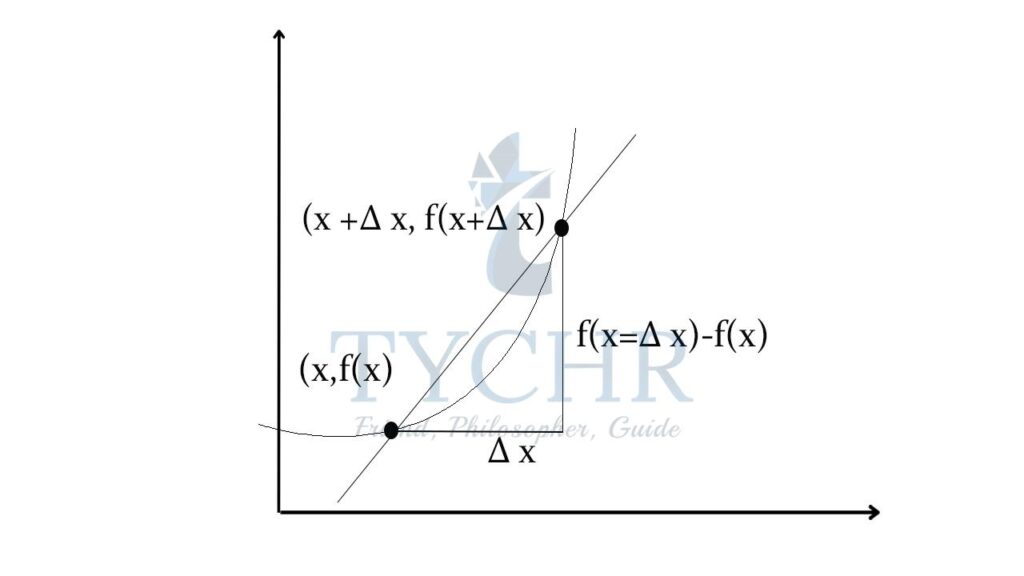

We know that the average rate of change is = Change in y / Change in x

which is also equal to the slope of the curve. 

For a straight line, the slope is constant, but for a curve, it changes at every point.
In the given graph, we have taken 2 points to find the rate of change, (x, f(x)) and (x+∆x, f(x+∆x))
Average rate of change = ∆𝑦∆𝑥 = (𝑓(𝑥+∆𝑥)−𝑓(𝑥)) / ∆𝑥

Here, the line joining the 2 points is the secant line.
Now, when it comes to calculating the instantaneous rate of change, we need those 2 points to be very very close!
Which means the line joining the 2 points will become a line passing through just 1 point. That line is the tangent line to the curve and the slope of this line will be the instantaneous rate of change. The change ∆x will tend towards zero!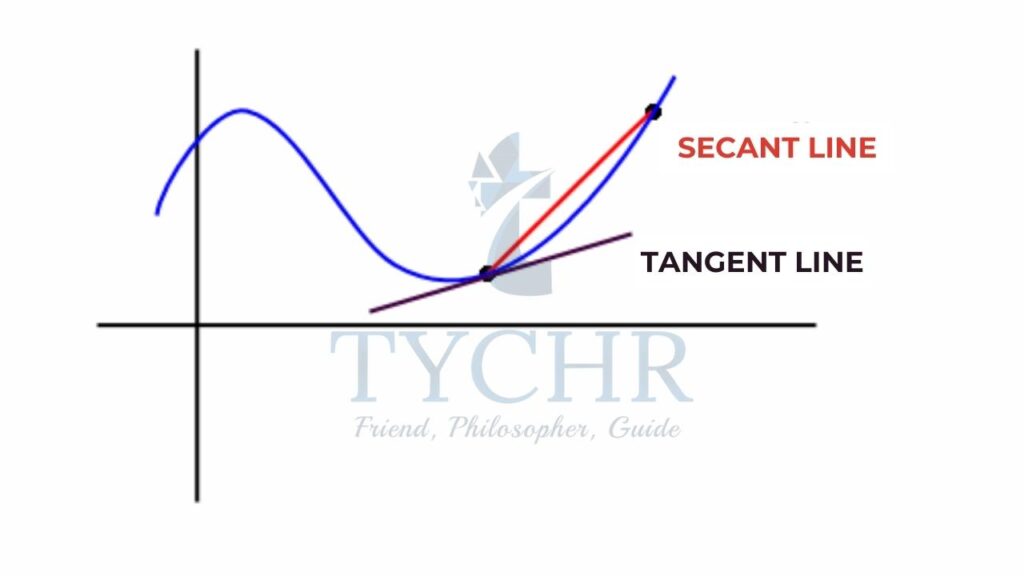

We define the derivative of a function f as:f^’ (x)=lim┬(∆x→0)⁡〖(f(x+∆x)-f(x))/∆x〗 Provided that this limit exists. 
We will learn about limits in detail in the next section.

LIMITS AND CONVERGENCE 

• Limit– A value we get closer and closer to, but never quite reach.
  For example, when we graphy = (1/x),  we see that it gets closer… and closer… to zero but does not ever quite get there.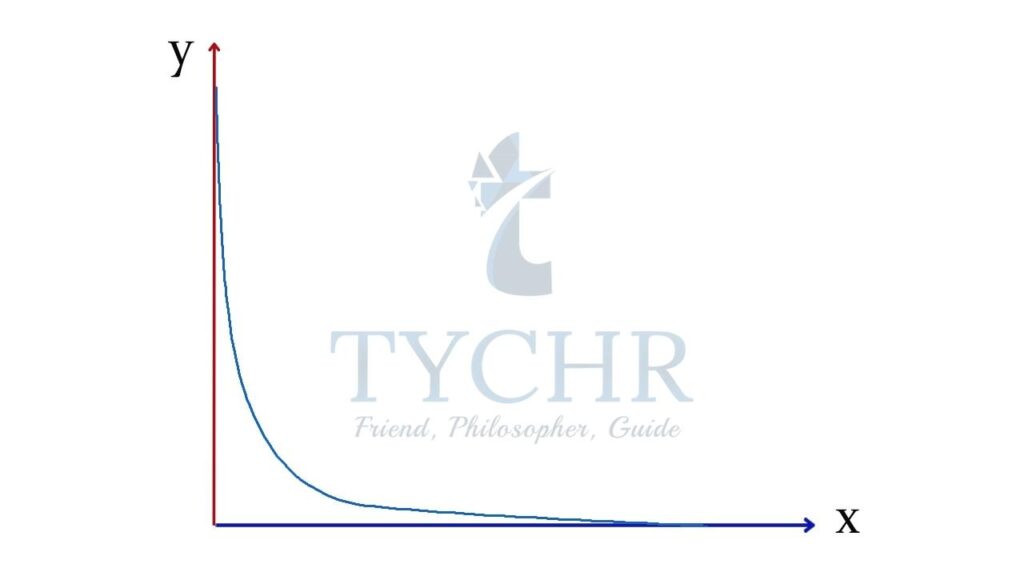
  We then say “As x approaches infinity, then (1/x) approaches 0”
  And write it like this: 1/x = 0
• One sided limit- 

• • One-sided limits are those limits that only converge to a single value on one side of a function. 
  • For a function f(x), the left hand limit is defined as x approaches some value a from the left, or negative, side: 𝐥𝐢𝐦_{𝒙→𝒂−}𝒇(𝒙)
  • The right hand limit is defined as x approaches the same value a from the right, or positive, side: 𝐥𝐢𝐦_𝒙→𝒂+𝒇(𝒙)

• When limit does not exist-
  A common situation where the limit of a function does not exist is when the one-sided limits exist and are not equal: the function “jumps” at the point.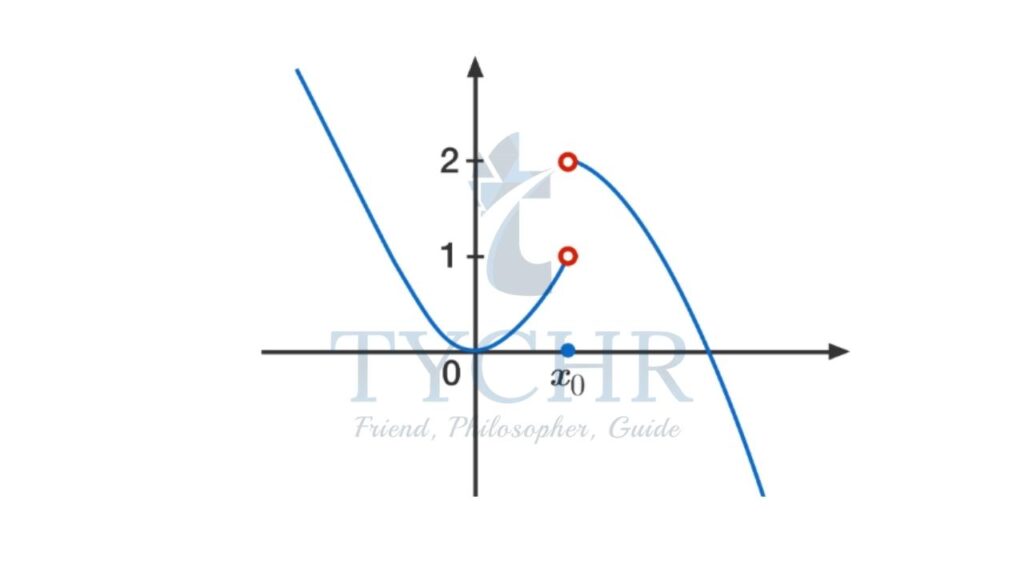
  For the function f in the picture, the one-sided limits f(x) and f(x) exist but are not equal, which is the requirement for the limit to exist.
  This is usually written as:
  f(x) =DNE
  where “DNE” stands for “does not exist.”
• Limits of sequences
  Recall the formula for finding the sum of finite geometric series: S_n = u₁(1-rⁿ)/(1-r) When |r|<1, then u₁(1-rⁿ)/(1-r) = u₁/(1-r)

Ex. Evaluate (x²-1)/(x-1)

If we will put x=1 directly in the function, we will get 0/0, which is not defined.
So, instead we solve the function first:(x²-1)/(x-1) = ((x+1)(x-1))/(x-1) = (x+1) Now, we can put x=1 in the function, we get:(x²-1)/(x-1) = 2

Ex. Evaluate sinx/x At x=0 both sin x and x will be 0 and the function will not be defined. So to find out the one sided limits, we look at the graph of y = sinx/x: 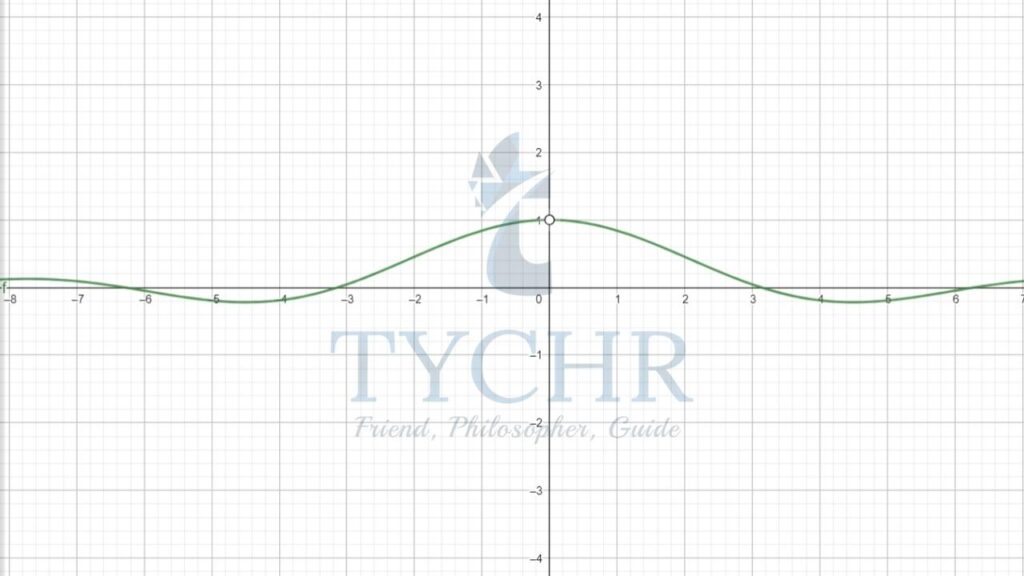Looking at the graph sinx/x =1 and sinx/x Hence, sinx/x = 1.

Ex. Evaluate (1-cosx)/x

Multiply the numerator and denominator by ((1+cos x )(1-cosx))/x(1+cosx) = (1-cos²x)/x(1+cosx) = sin²x / (1+cosx)x
From previous result sinx/x = 1 Using this result, we will get 1(sinx/(1+cosx) Putting x=0, we get zero as the answer.(1-cosx)/x

Ex. Evaluate lim_(x→∞)⁡(-2x+3)/(x+1) and lim_(x→-1)⁡(-2x+3)/(x+1)
lim_(x→∞)⁡(-2x+3)/(x+1) To solve this, we divide the numerator and denominator by x: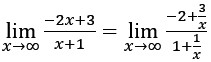 The terms with x in the denominator will tend to zero, and the value of the limit will be: lim_𝑥→∞ (−2𝑥+3)/ (𝑥+1) = − 2/1 = −2
lim_𝑥→−1 (-2𝑥+3)/(𝑥+1)

Looking at the function, we cannot solve it any further, the denominator will tend to zero as x tends to -1, and hence the function will tend to infinity. lim𝑥→−1 (-2𝑥+3)/(𝑥+1) = ∞ Observe both the limits carefully, it says that when x is tending to infinity, the function tends to -2, recall from previous chapter, this clearly means that y=2 will a horizontal asymptote to the function 𝑦 = (−2𝑥+3)/(𝑥+1)

Also, as x tends to -1, the function is tending to infinity, which also clearly means thar x=-1 is a vertical asymptote to the function 𝑦 = (−2𝑥+3)/(𝑥+1)

We can easily graph the function 𝑦 = (−2𝑥+3)/(𝑥+1)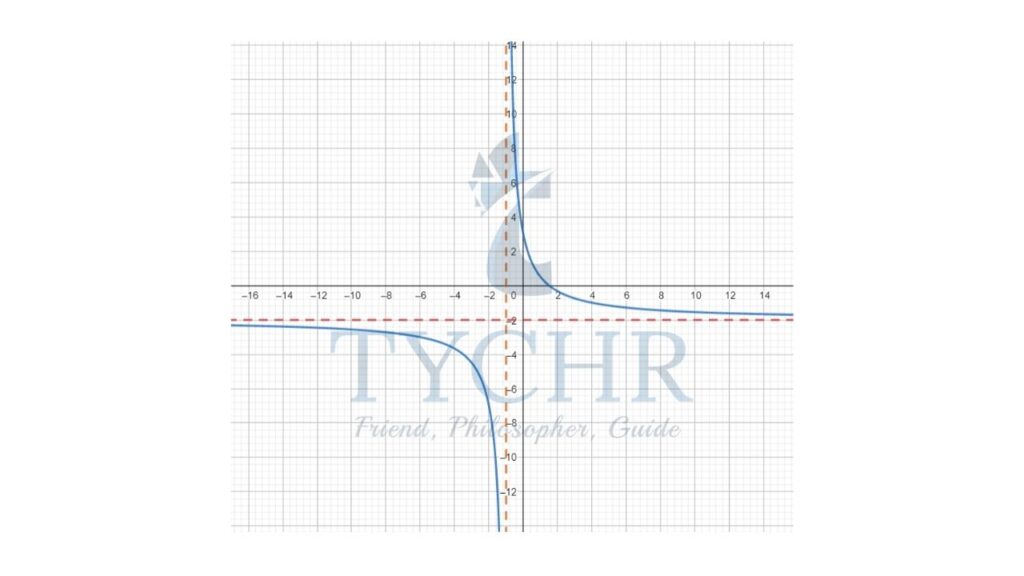

THE DERIVATIVE OF A FUNCTION

TANGENT LINE AND SLOPE

We defined the derivative of a function f as- 𝒇 ′ (𝒙) = (𝒇(𝒙+∆𝒙)−𝒇(𝒙))/∆𝒙

Where f‘(x) the derivative, is the instantaneous rate of change at point x on the curve and is also the slope of the tangent line at that point.

• f‘(x) is called “f dash x” or “f prime of x”
• dy/dx means “the derivative of y with respect to x”

BASIC DIFFERENTIAION RULES

1. The power rule for differentiation:
   If n is any real number and f(x)=xⁿ, then f'(x)=nx^n-1,  (n∈Q)

Ex. Find the derivative of f(x)=x¹¹
The power of the function is 11
f'(x)=11x¹⁰ 

Ex. Find the derivative of f(x)= 𝑓(𝑥) = 1/𝑥^3/2 The power of the function is -3/2
𝑓 ′ (𝑥) = (− 3/2) (𝑥)^{(−3/2) −1} 𝑓 ′ (𝑥) = −(3/2) 𝑥^−5/2 

1. Derivative of a constant
   𝒅(𝒄)/𝒅𝒙 = 0 ,  (c∈R)
2. Derivative of a constant multiple of a function
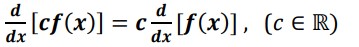    ,   (c∈R)
3. Derivative of the sum or difference of functions
   

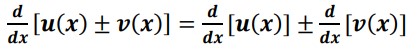
Ex. Find the derivative of 𝑓(𝑥) =(4𝑥²+𝑥−3)/𝑥 
𝑓(𝑥) = (4𝑥²/𝑥) + (𝑥/𝑥) − (3/𝑥)
𝑓(𝑥) = 4𝑥 + 𝑥⁰ − 3/𝑥
𝑓 ′ (𝑥) = 𝑑 /𝑑𝑥 (4𝑥 + 𝑥⁰ − 3/𝑥 )
𝑓 ′ (𝑥) = 𝑑(4𝑥)/ 𝑑𝑥 + 𝑑(𝑥⁰)/𝑑𝑥+ 𝑑(− 3/𝑥)/ 𝑑𝑥
𝑓 ′ (𝑥) = 4 𝑑(𝑥)/𝑑𝑥 + 𝑑(𝑥⁰)/𝑑𝑥 − 3 𝑑( 1/𝑥 )/𝑑𝑥
𝑓 ′ (𝑥) = 4(1)𝑥⁰ + 0(𝑥)⁻¹ − 3(−1)𝑥⁻²
𝑓 ′ (𝑥) = 4 + 3/𝑥²

DERIVATIVES OF SINE AND COSINE FUNCTION

1. Sine function 𝒅(𝐬𝐢𝐧 𝒙)/𝒅𝒙 = 𝐜𝐨𝐬 𝒙 Let’s prove this graphically:
   We know that the derivative at a point is also the slope of the tangent line at that point. Graphing sine function and marking the slope of the tangent line at some points: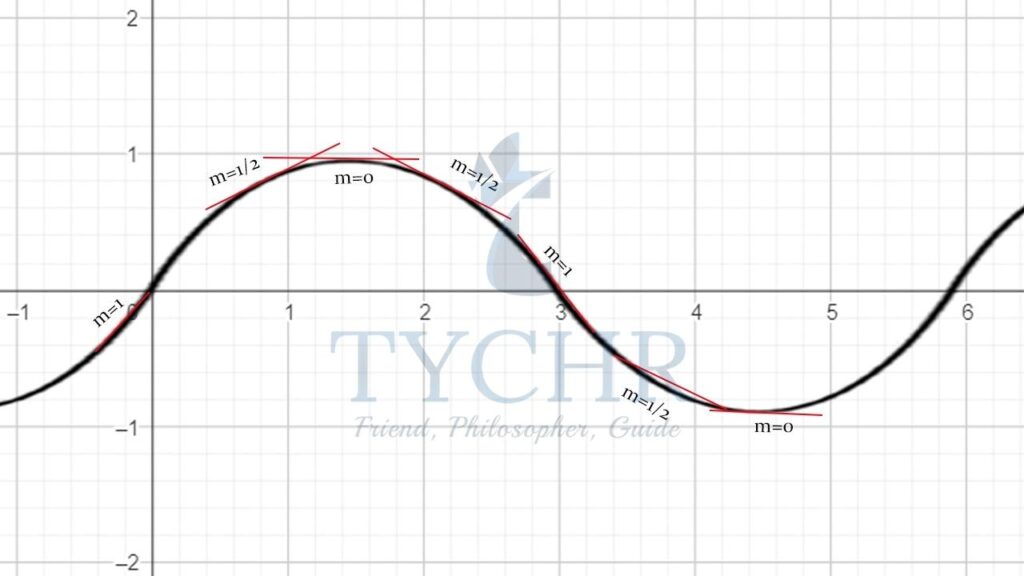
   Taking as many points as we can and plotting the slope at each point as the y-value on the graph, we will get the graph of y=cos x :
   Hence the derivative of f(x)=sin x will be f'(x)=cos x .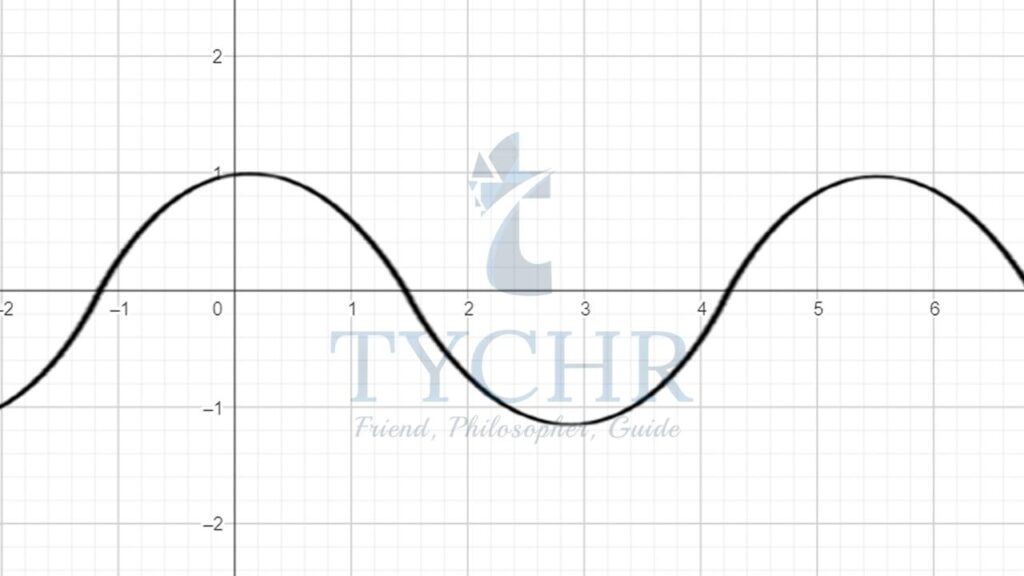
2. Cosine function 𝒅(𝐜𝐨𝐬 𝒙)/𝒅𝒙 = − 𝐬𝐢𝐧𝒙 This can also proved graphically just like the previous one. We will try to prove by our knowledge of trigonometry.
   Putting:Hence, cos(-x) = sin(x)

Ex. Find the derivative of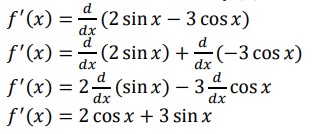

GRAPHICAL INTERPRETATION OF FIRST AND SECOND DERIVATIVES

INCREASING AND DECREASING FUNCTIONS

• The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain.
• When a function is increasing, its derivative (its “slope”) is positive, and when the function is decreasing, its derivative is negative.
• So if we want to find the intervals where a function increases or decreases, we differentiate it and find the intervals where its derivative is positive or negative.
• Critical points are the points where f’ is zero or undefined.
• This method of checking if the function is increasing or decreasing and about which point is called the first derivative test.

Ex. Let’s find the intervals where f(x)=x³+3x²-9x+7 is increasing or decreasing. First, we differentiate f(x): 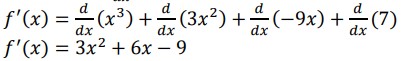Now we want to find the intervals where f‘(x) is positive or negative. This is done using critical points, which are the points where f‘(x) is either 0 or undefined. f‘(x) is a polynomial, so it’s always defined. To find its zeros, we can factor it: 𝑓 ′ (𝑥) = 3(𝑥 + 3)(𝑥 − 1)

These points divide the number line in three parts:
f'(x) will be positive in the intervals ]-∞,-3[ and  ]1,∞[

and will be negative in ]-3,1[

GLOBAL AND LOCAL MAXIMA OR MINIMA

• We denote maxima or minima as either global or local.
• Simply writing maxima or minima is confusing and are taken to be the global ones by convention.
• A maximum or minimum is said to be local if it is the largest or smallest value of the function, respectively, within a given range.
• However, a maximum or minimum is said to be global if it is the largest or smallest value of the function, respectively, on the entire domain of a function.
• There is only one global maxima and only one global minima.
• There can be multiple local maxima and minima
• A global minima or maxima is also a locak maxima or minima.

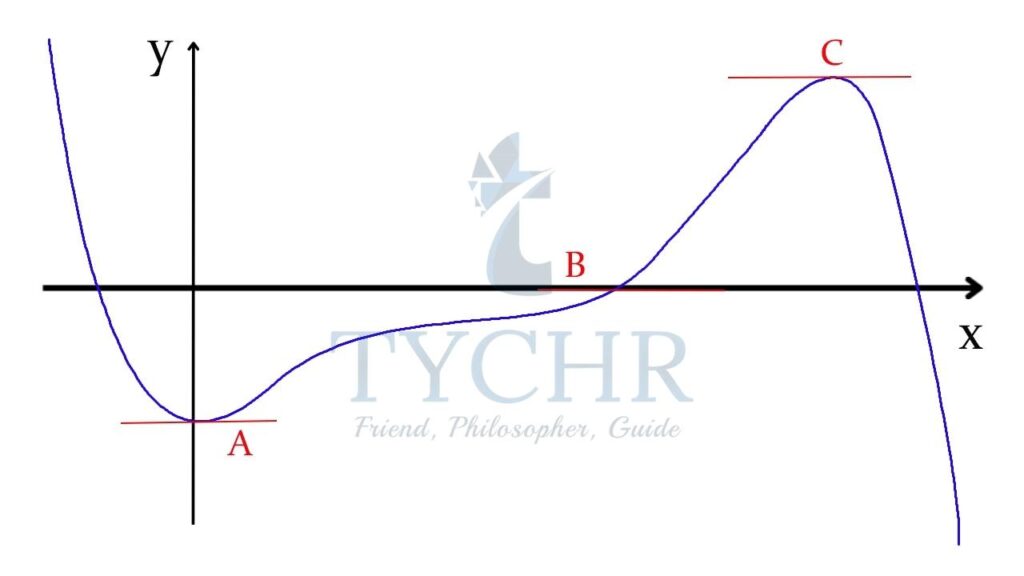
STATIONARY POINT (POINT OF INFLECTION)

• These are critical points of a function. These are the points where f‘(x) or the slope of the curve is zero.
• These points are called “stationary” because at these points the function is neither increasing nor decreasing. 
• Graphically, this corresponds to points on the graph of f(x) where the tangent to the curve is a horizontal line.
• A stationary point is called a turning point if the derivative changes sign (from positive to negative, or vice versa) at that point.
• A point where the derivative of the function is zero but the derivative does not change sign is known as a point of inflection, or saddle point.
• In the diagram below, A and C are turning points and B is a saddle point.
  
  

Ex. f(x)=4-3x²+x³  for -2≤x≤3. Find stationary points and their nature, intervals for which the function is increasing or decreasing, and identity the critical points as local or global extrema. 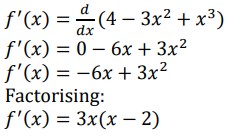For critical points f'(x)=0
3x(x-2)=0 
x=0 and x=2

These points will create 3 intervals:

At x=0, f(x)=4
At x=2, f(x)=0
(0,4) is a local maximum point
(2,0) is a local minimum point.

According to the domain:
f is increasing for x∈[-2,0 ∪ 2,3]
f is decreasing for x∈ ]0,2[

Checking y-values for end points of domain
f(-2)=-16 
which is less than the minimum point that we calculated, hence (-2,-16) is the global minima.
f(3)=4 
f(0)=f(3)=4 and hence both are a local and global.

FUNCTION AND ITS SECOND DERIVATIVE

• Given a function f(x), the derivative f‘(x) is known as the first derivative of f(x). The gradient of the first derivative, f”(x) is called the second derivative of f(x).
• 𝑓(𝑥) = 𝑦, 𝑓′(𝑥) = 𝑑𝑦/𝑑𝑥 , 𝑓′′(𝑥) = 𝑑²𝑦/𝑑𝑥² 
• The second derivative may be used to determine local extrema of a function under certain conditions. 
• If function has a critical point for which f'(x)=0 and f”(x)<0 then f(x) has a local maxima here.
• If function has a critical point for which f'(x)=0 and f”(x)>0 then f(x) has a local minima here.
• This technique is called Second Derivative Test for Local Extrema.
• Three possible situations could occur that would rule out the use of the Second Derivative Test for Local Extrema:
  1. f'(x)=0 and f”(x)=0
  2. f'(x)=0 and f”(x) does not exist
  3. f‘(x) does not exist

Ex. Find any local extrema of f(x)=x⁴-8x²
𝑓′(𝑥) = 𝑑 (𝑥⁴ − 8𝑥² )/𝑑𝑥
f'(x)=4x³-16x 

Factorising: f'(x)=4x(x²-4)
𝑓′(𝑥) = 4𝑥(𝑥 − 2)(𝑥 + 2)
f‘(x) will be zero at x=0, x=2, x=-2
f(0)=0 
f(2)=-16 
f(-2)=-16 
(0,0), (2,-16) and (-2,-16) are stationary points.

𝑓′′(𝑥) = 𝑑(4𝑥³ − 16𝑥)/𝑑𝑥
f”(x)=12x²-16 
f”(0)=-16 
(0,0) is a local maxima.
f”(2)=32 
(2,-16) is a local minima.
f”(-2)=32 
(-2,-16) is a local minima.

CURVE SKETCHING 

We can sketch the curve of f‘(x) and f”(x), when the curve of f(x) is given.

Ex. The graph of y=f(x) is given below:

To graph y=f‘(x), we keep in mind the following points: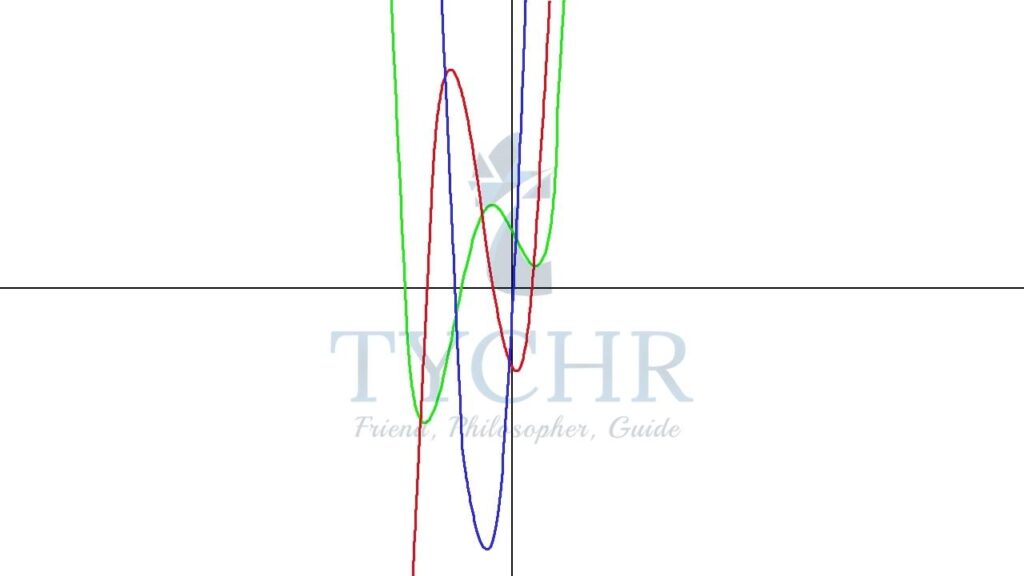

• The turning points of f(x) are the zeros f‘(x).
• The intervals where f(x) is increasing will be the intervals where f‘(x) is positive.
• The intervals where f(x) is decreasing will be the intervals where f‘(x) is negative.

Graphing f‘(x):

To graph y=f”(x), we keep in mind the following points: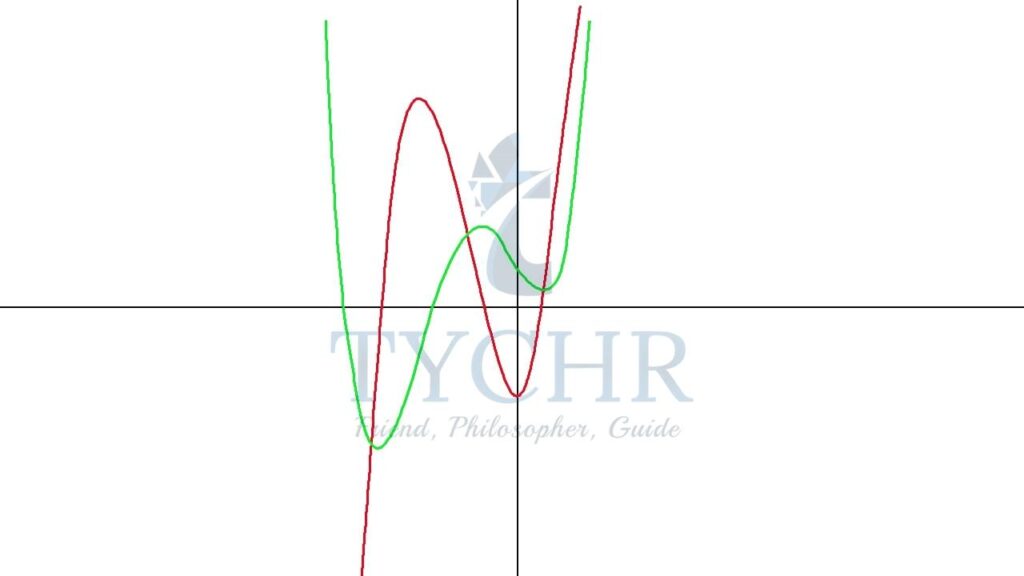

• The turning points of f‘(x) are the zeros f”(x).
• f”(x) will be positive when f(x) is concave up.
• f”(x) will be negative when f(x) is concave down.

TANGENTS AND NORMAL

• A tangent to a cruve is a line that touches the curve at one point and has the same slope as the curve at that point.
• A normal to a curve is a line perpendicular to a tangent to the curve.
  
  

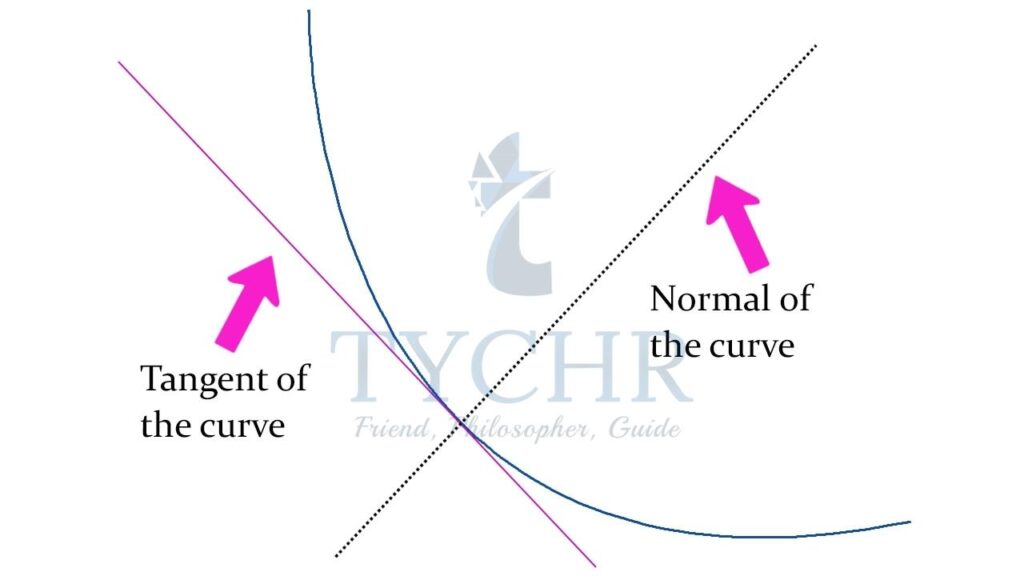
FINDING EQUATION OF TANGENT

Given a function y=f(x), the equation of the tangent to this curve at x=x₀ can be found in the following way:

• Find out the gradient/derivative of the curve at the point x=x₀. This will give us the slope of the tangent (m).
• Use the point-slope form of line to find the equation of tangent at (x₀,y₀)
  y-y₀=m(x-x₀) 

FINDING EQUATION OF NORMAL

Steps for finding the normal to a given curve y=f(x) at a point x=x₀:

• Find out the gradient/derivative of the curve at the point x=x₀. This will give us the slope of the tangent (m).
• Normal is a line perpendicular to tangent, therefore the slope of the normal (n) will be- n = -(1/m)
• Use the point-slope form of line to find the equation of normal at (x₀, x₀) 
  𝑦 − 𝑦₀ = (−1/𝑚) (𝑥 − 𝑥₀)
  

Ex. Consider the curve given by y=f(x)=x³-x+3.  

1. Find the equation of the line tangent to the curve at the point (1,3). 
2. Find the line normal to the curve at the point (1,3)

Finding the derivative of the function:
𝑓′(𝑥) = 𝑑(𝑥³ − 𝑥 + 3)/𝑑𝑥
f'(x)=3x²-1 

The slope of the tangent m=f‘(1)=3(1)²-1=2
Equation of tangent at (1,3):

The slope of normal n =-1/m =-(1/2)n

Equation of normal at (1,3)
𝑦 − 3 = (−1/2) (𝑥 − 1)
2𝑦 − 6 = −𝑥 + 1
𝟐𝒚 + 𝒙 = 𝟕