This section deals with mathematical modelling of physical quantities related to motion and graphical representation of appropriate quantities for better understanding.

Motion

Displacement and distance:

Displacement is the length of the shortest path (which is a straight line) between two points.

• It is a vector. Direction has to be mentioned along with length in appropriate units.
• SI unit is metre (m).

Distance is the length of the path travelled.

• It is a scalar.
• SI unit is metre (m).

Velocity and speed:

Velocity is displacement per unit time.

• velocity = displacement / time
• Velocity is the rate of change of a vector. So, it is also a vector quantity.
• SI unit is m s^-1.

Speed is distance travelled per unit time.

• speed
• It is a scalar quantity.
• SI unit is m s^-1.

Constant velocity means that the velocity remains constant with time. The difference between constant velocity and constant speed is to be understood. Constant velocity requires that the direction also does not change along with magnitude.

Average and instantaneous values:

Average speed is the total distance travelled divided by the total time taken.
Instantaneous speed is the rate of change of position with respect to time.
Mathematically,
average speed = total distance / total time taken = ∆s/∆t
and instantaneous speed = time derivative of distance = ds/dt

The same implies for velocities with appropriate directions. The direction of instantaneous velocity is the tangent to the path at that point and that of average velocity is the line joining initial and final points of journey.

Graphically, the instantaneous speed is the gradient of the tangent at a point and average speed is the gradient of the line joining initial and final points in a distance-time graph.

E.g.: The graph shows the distance run by a boy in accordance with time.

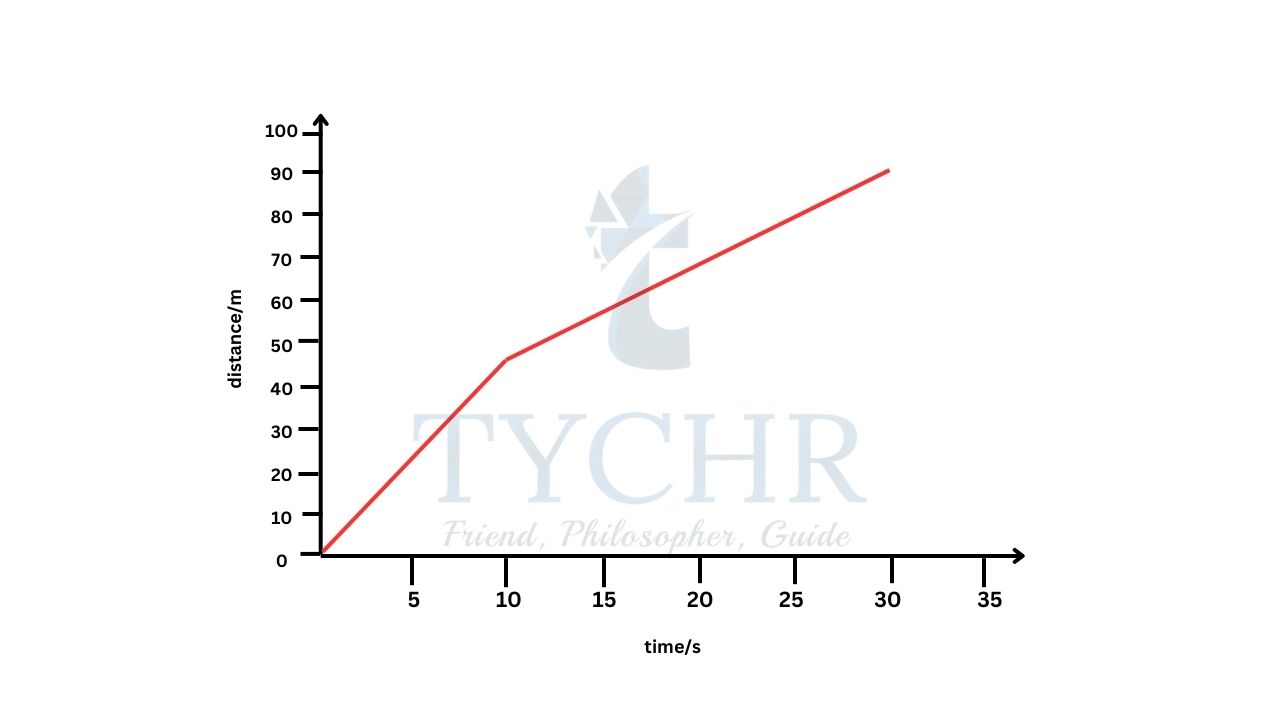
Calculate

a.) the instantaneous speed at

a. 5.0s  b. 20s

b.) The average speed for the whole 30s run

Answer. 
a) The boy runs with a constant speed from 0-10s.
So, the instantaneous speed is the gradient of 0-10s line.

instantaneous speed at 5.0s = (48−0)/(10−0) = 4.8 ms^-1

The boy runs with a constant speed from 10-30s.

So, the instantaneous speed is the gradient of 10-30s line.

instantaneous speed at 20s = (90−48)/(30−10) = 2.1 ms^-1

b) average speed is the total distance travelled divided by total time, which is (90/30) = 3.0 m s^-1.

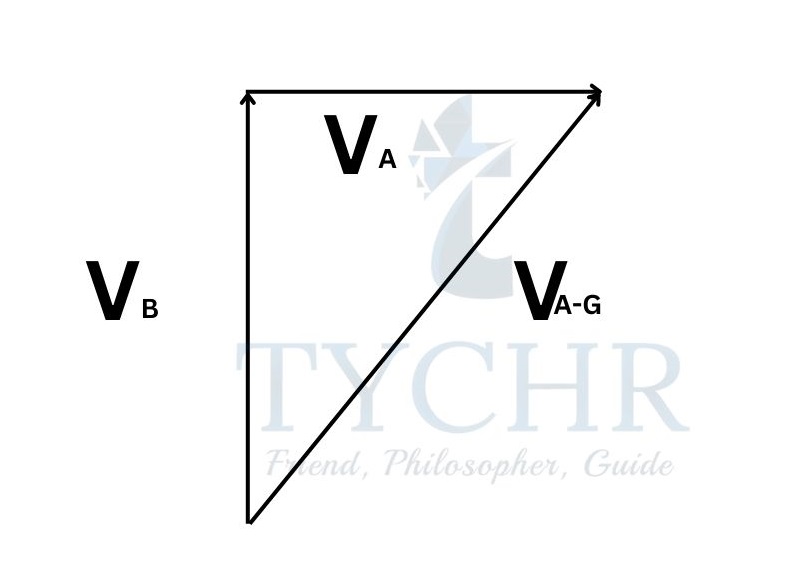
Relative velocity:

Velocity is a vector quantity. So, it must be added vectorially. If you are moving with a velocity v_A (with respect to vehicle) on a vehicle moving with a velocity v_B, then your velocity with respect to ground is the vectorial sum of v_A and v_B.

Acceleration:

Acceleration is the rate of change of velocity.
acceleration = change in velocity/time = (v − u)/t

• It is a vector quantity.
• SI unit is m s^-2.
• A body is said to accelerate if moves faster, slower (deceleration) or it’s direction of motion changes.
• When a body is decelerating, the direction of acceleration is opposite to the direction of velocity.

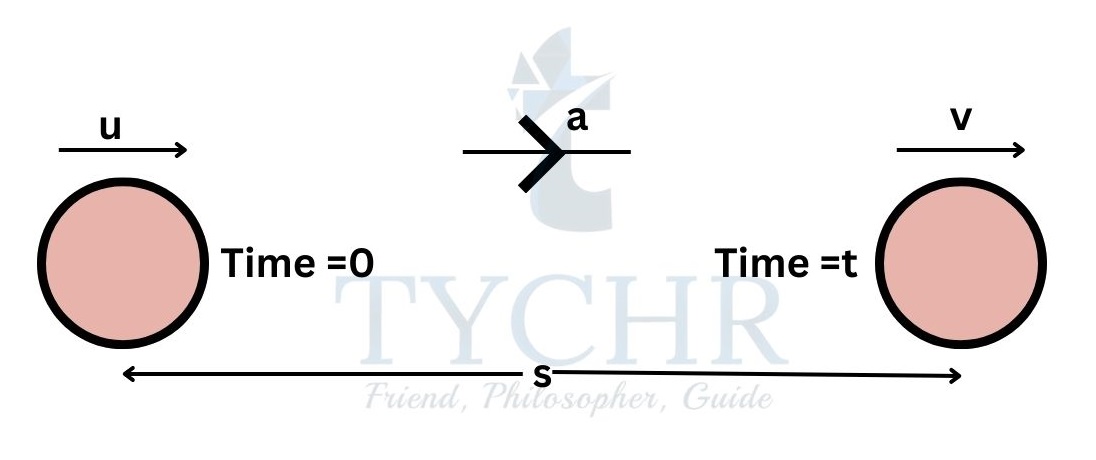
The “suvat” equations of motion:

Here s is distance, u is initial velocity, v is final velocity, t is time taken and a is the acceleration of the body (assumed to be constant).

Rearranging the terms of acceleration definition, we get
𝑣 = 𝑢 + 𝑎t    -1^st equation of motion 
average velocity =s/t=(v+u)/2 ,

rearranging the above 2 equations,
𝑠 = 𝑢𝑡 + (1/2)𝑎𝑡²    -2^nd equation

rearranging equations 1^st equation and equation of average velocity,
v² − u² = 2as   -3^rd equation

E.g.: A car travelling at 10 ms^-1 accelerates at 2 ms^-2 for 5s. what is its displacement?.

Answer. u=10 ms^-1
a=2 ms^-2
t=5s

using the equation 𝑠 = 𝑢𝑡 + (1/2)𝑎𝑡² ,
the displacement can be calculated to be 75m.

Sign convention:

In a single dimensional motion, the direction towards the right is considered. This is arbitrary and can be modified according to the ease of the problem.

Displacement towards the right is positive Velocity is positive if the motion is towards the right.

Acceleration is positive if the motion is towards right and the body speeds up or motion is towards left and the body slows down.

Problems regarding motion should be solved considering the above sign conventions.

E.g.: A body with a constant acceleration of -5 ms^-2 is travelling to the right with a velocity of 20 ms^-1. What will be the displacement after 20s.

Answer. u=20 ms^-1
t=20s
a=-5 ms^-2

from the equation,
𝑠 = 𝑢𝑡 + (1/2)𝑎𝑡²
it can be calculated that s=-600m.

this means that the final displacement is to the left of the starting point. But the initial velocity is towards right. This implies that the body has gone forward by a distance, stopped and then gone backwards.

Graphical representation of motion:

Displacement-time graph:

The gradient of the displacement-time graph is ds. Thus, the gradient of the displacement-time graph gives dt velocity.

Velocity-time graph:

Gradient of the velocity-time graph gives dv, which is acceleration. dt.

Area under the velocity-time graph is v∆t. This is displacement

Acceleration-time graph:

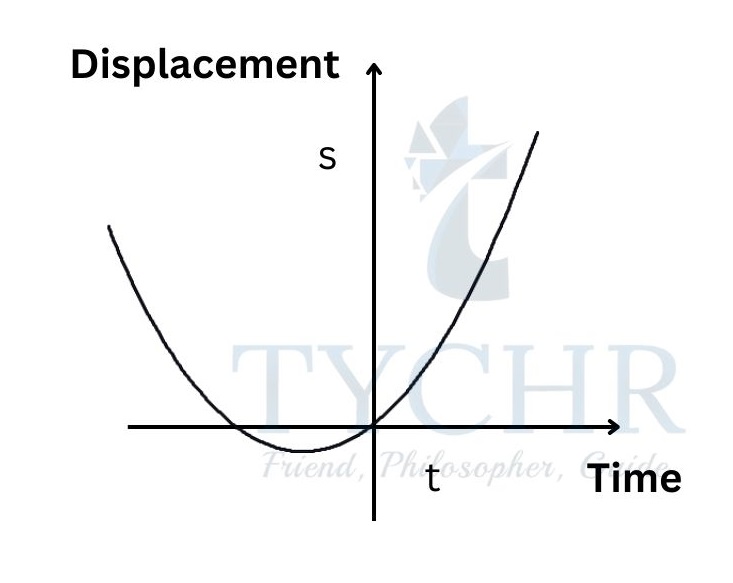
Area under the acceleration-time graph is a∆t. This is a change in velocity (v-u). E.g.: Consider the following motion of a ball

Represent the displacement, velocity and acceleration of the ball graphically.

Displacement-time:

The ball moves with constant acceleration with an initial velocity u. The equation 𝑠 = 𝑢𝑡 + (1/2)𝑎𝑡². represents the displacement of the ball with time and the graph is a parabola.

Velocity-time:

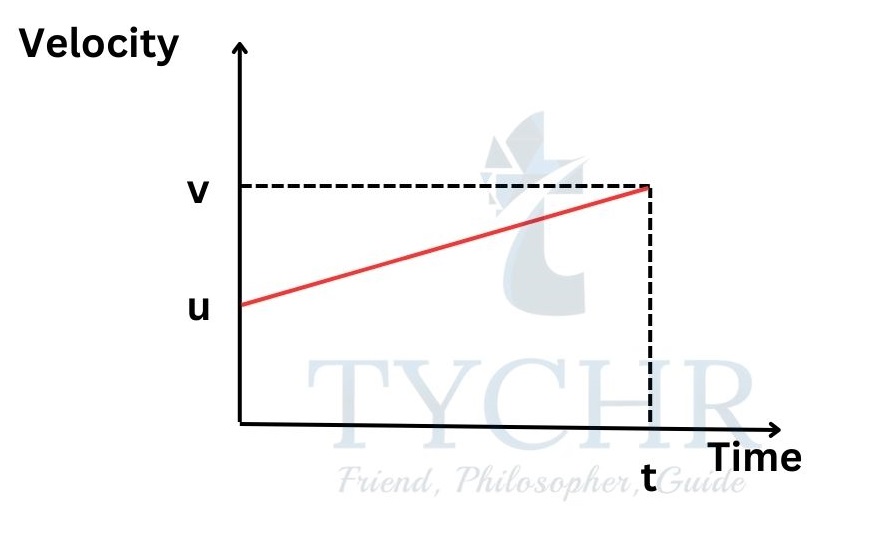
The equation representing velocity with respect to time is 𝑣 = 𝑢 + 𝑎𝑡.

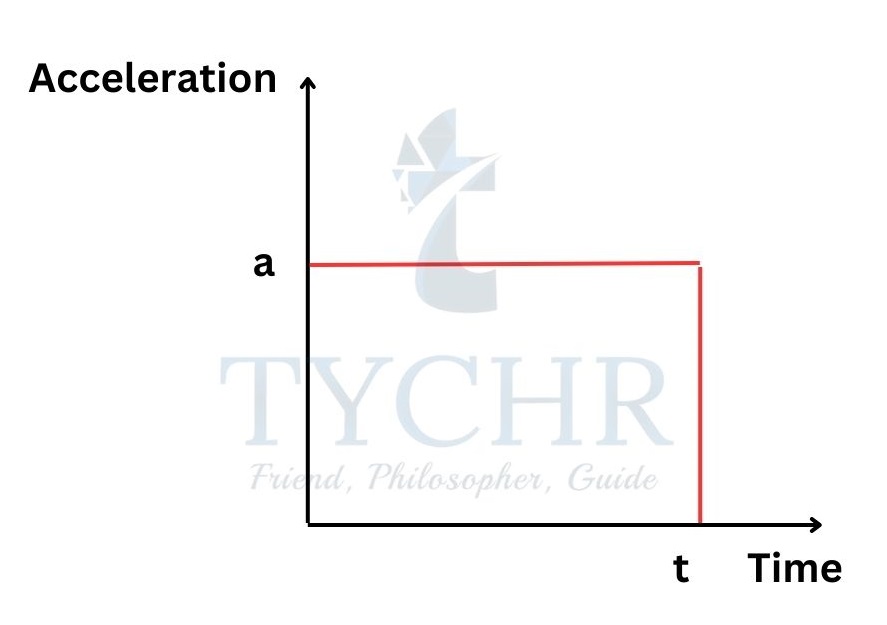
Acceleration-time:

The body moves with a constant acceleration.

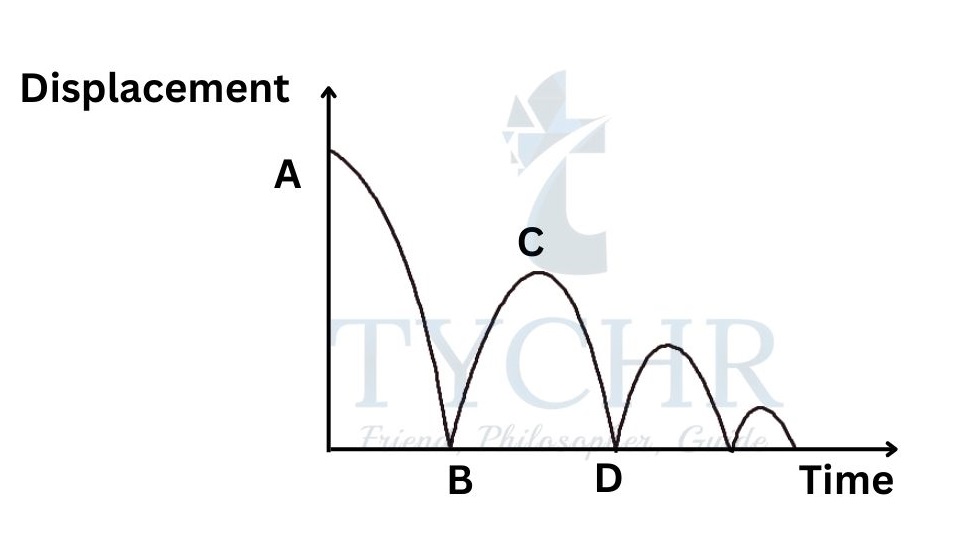
E.g.: Consider a ball dropped onto a floor. The ball falls with increasing speed and bounces back (to a lesser height) with decreasing speed  and this process repeats itself until the ball comes to a complete stop.

Modelling projectile motion:

Consider a ball projected with an initial velocity v at an angle θ with the ground. The ball faces a constant acceleration due to gravity in the downward direction. This has an average value of 9.81 ms^-2 and is represented by g. The trajectory traced by the body is a parabola. It is to be noted that this motion is considered to be unaffected by air resistance and is performed at small heights.

Few parameters are stated below for a projected body.

Range =𝑅 =𝑣²𝑠𝑖𝑛2𝜃/g
Vertical height 𝐻 =𝑣²𝑠𝑖𝑛2𝜃/2g
Time of travel t= 2𝑣𝑠𝑖𝑛𝜃/g

E.g.: A ball is projected with a velocity of 20 ms^-1 at an angle of 30˚ with the horizontal. Find the range and maximum height reached by the ball.

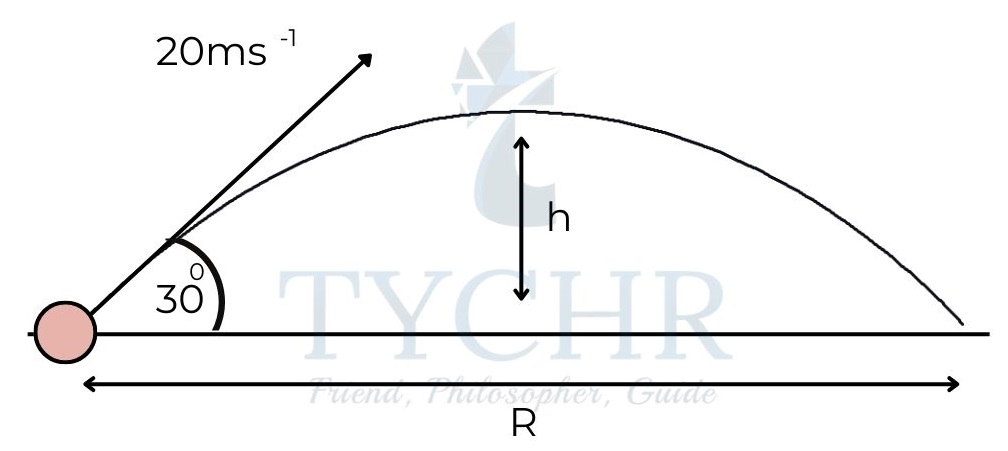
Ans: Here, v=20 ms^-1 and θ=30˚
From the equations, 𝑅 = 𝒗²𝒔𝒊𝒏𝟐𝜽/𝒈
and 𝑯 =𝒗^𝟐𝒔𝒊𝒏𝟐𝜽/𝟐g

R=20²×sin(2×30)/9.81 = 34.6m
And H=(20²×sin²30)/(2×9.81) = 5m

E.g.: An object is dropped from a hot air balloon moving with a velocity of 5 ms^-1 upwards at the instant it is 30m above ground.

a.) Calculate the maximum height reached by the object.

Answer. When the object reaches maximum height, it comes to a rest.
v=0, u=5 ms^-1, a=-9.81 ms^-2
From the equation v² − u² = 2as,
S= (0−5²)/(−2×9.81)=1.3m

So, the object reaches a height of 1.3m in addition to the 30m the calculation has been carried out from.
So, the total maximum height achieved is 31.3m.

b.) Calculate the time taken to achieve this height

Answer. v=u+at, from this equation, t= (0−5)/(−9.81) =0.51s

c.) Calculate the total time for the object to reach the ground.

Answer. Here, 𝒔 = 𝒖𝒕 +(𝟏/𝟐) 𝒂𝒕^𝟐. Here, s=-30m, u=5 ms^-1, a=-9.81 ms^-2

Substituting the values in the equation and solving gives 2 solution: 3.04s and -2.02s. 3.04s is the solution we are concerned with.

Try to understand the mathematical significance of the other solution.

Force, momentum and impulse

Force:

Force tries to change the state of motion of the body

• It is a vector quantity
• SI unit is newton (N) or kgms^-2.

Forces acting on a system can be added vectorially. Forces are usually divided into components on a cartesian system and then added for ease.

Free body diagrams:

Free body diagrams are drawn for a single body indicating all the forces acting on the body. The forces are to be drawn to scale.

E.g.: Free body diagram for a ball falling freely under gravity with no air resistance.

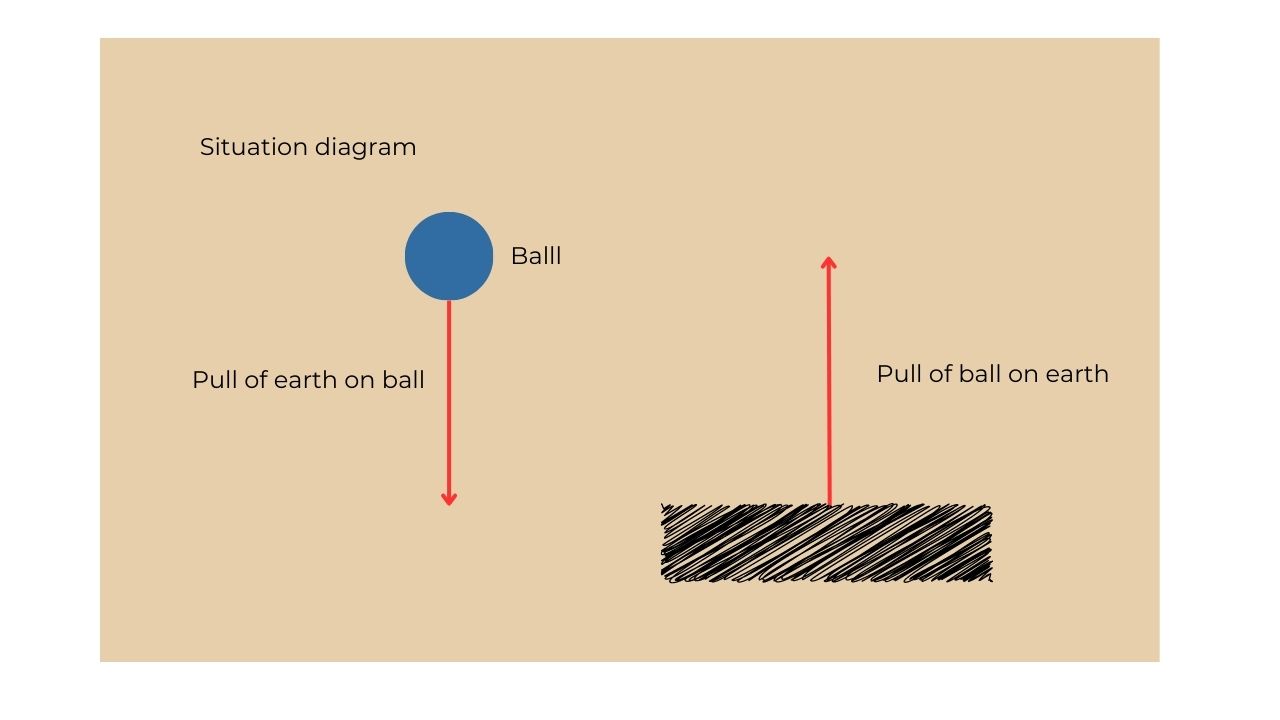
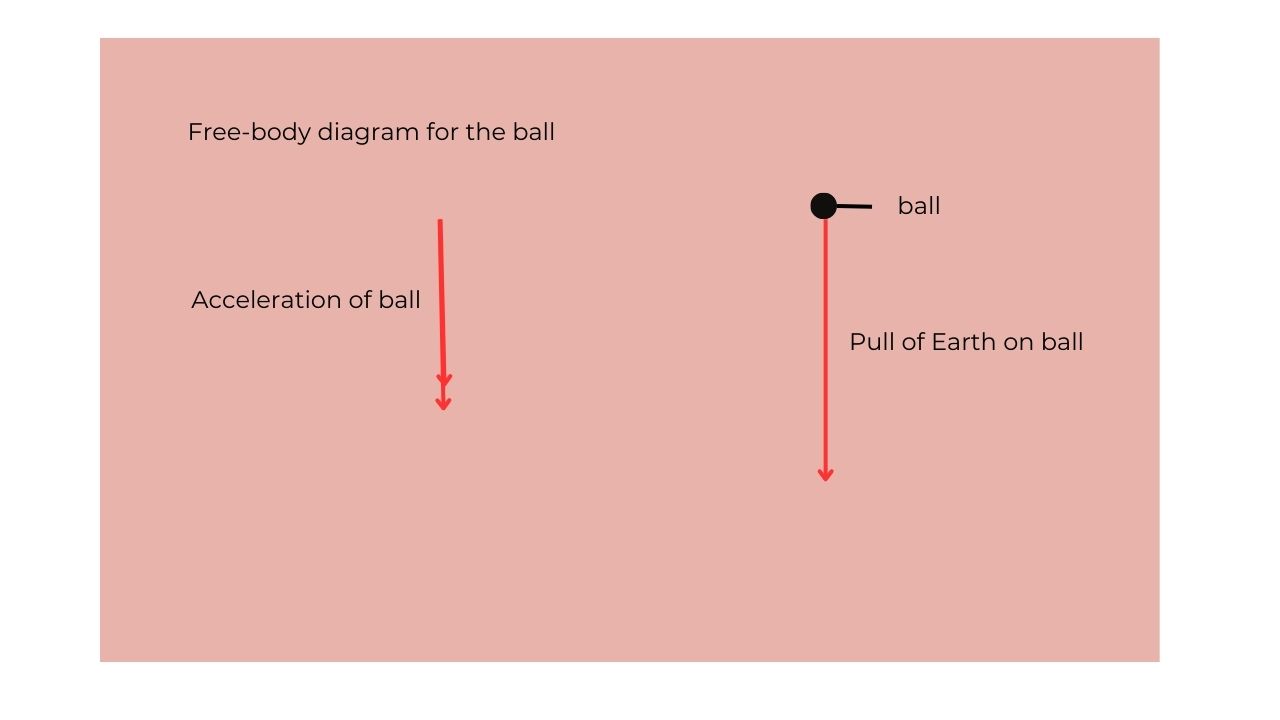
E.g.: A ball accelerating upwards in a lift.

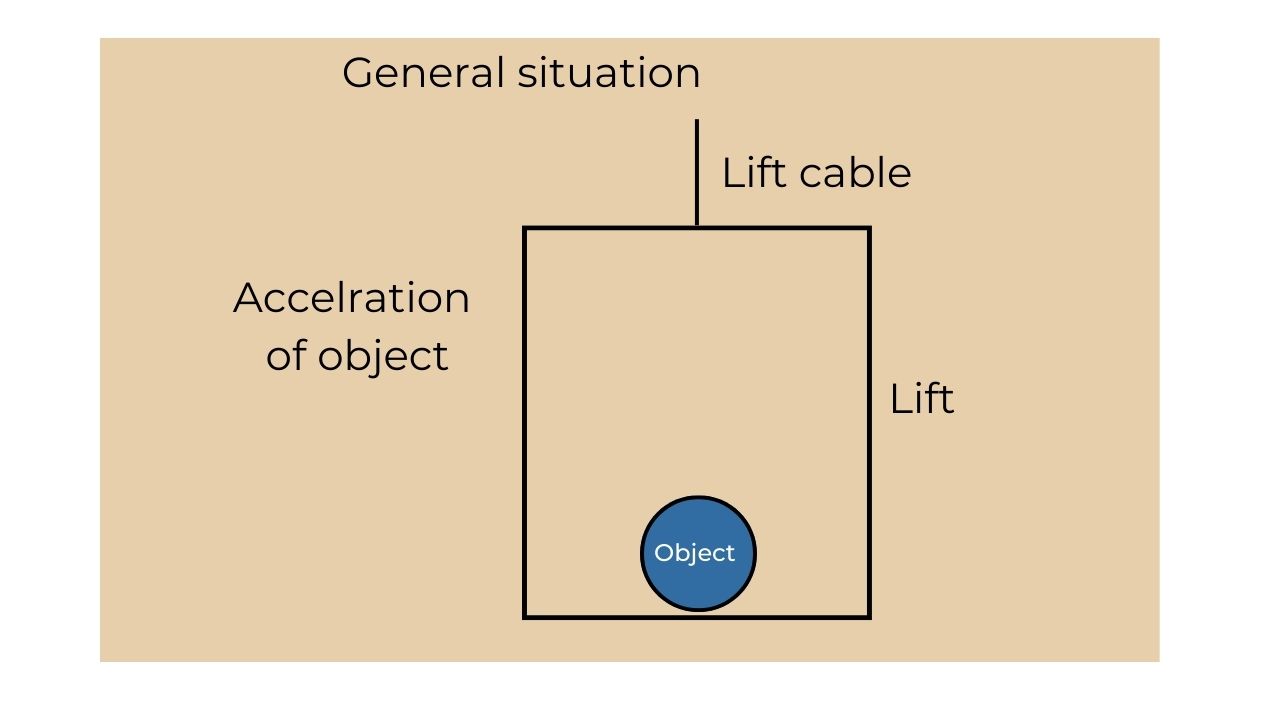
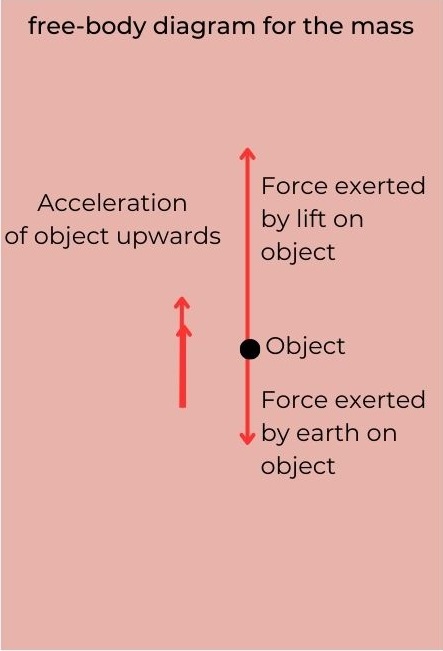
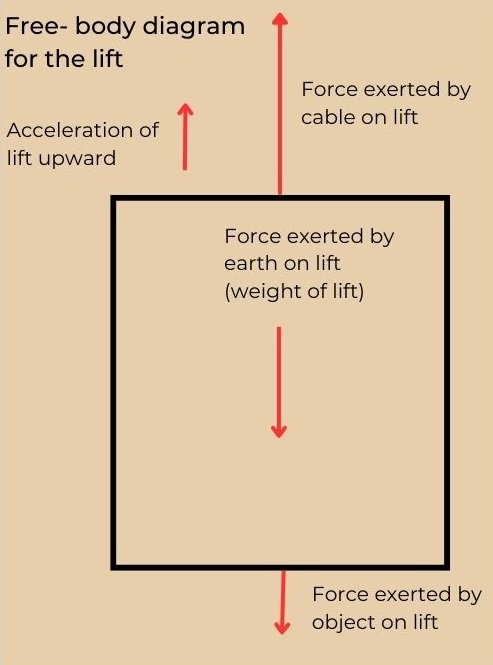
Translational equilibrium:

A system (an object or a group of objects) is said to be in translational equilibrium if the net force acting on the system is zero.

The object shown in the picture is said to be in a state of translational equilibrium since the net force acting on the object is zero.

Types of forces:

Tension:

Strings exert tension at one end when a pulling force is applied on the other end. Tension in strings can only apply pulling force.

Normal reaction:

Two objects in contact with each other exert a force on each other. This force is perpendicular to the surface of contact.

Gravitational force (weight):

The force exerted by the earth on objects around it causes an average acceleration of 9.81 ms^-2 if the air resistance is neglected.

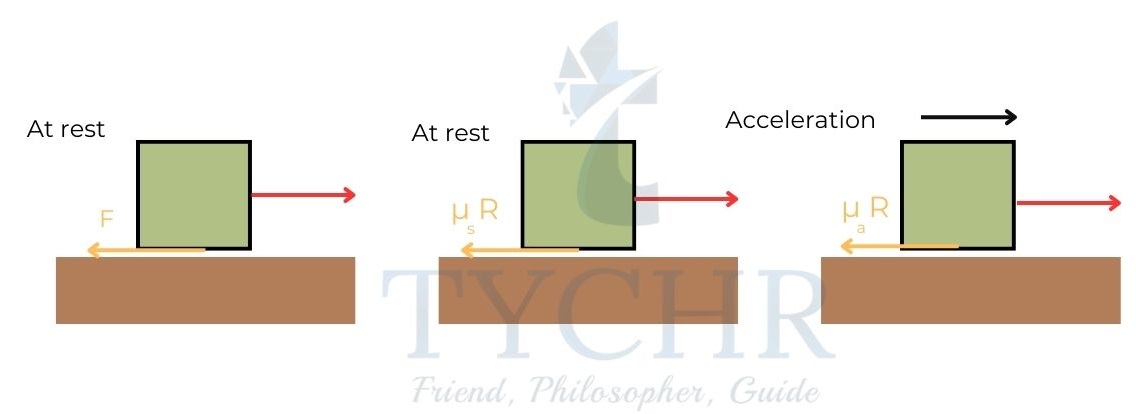
Friction:

There are two types of friction. Static and dynamic. In general, the frictional force between two objects can be described by

F=μR, where R is the normal reaction between the two objects and μ is called the coefficient of friction.

Static friction acts when the two bodies are in rest and force is acted to cause a relative motion between them.

Static friction equals the force applied until it reaches a maximum value and then friction fails to prevent the relative motion.

This maximum value of static friction can be described by the equation

F_s-max= μ_sR

μ_s is called the coefficient of static friction.

Once the motion is commenced, dynamic friction starts to act and it is independent of relative speed between the objects for small velocities.

F_d= μ_dR

μ_s is called the coefficient of dynamic friction.

Generally, μ_d< μ_s.

Buoyancy:

The force experienced by a body when it is fully or partially immersed in a fluid is called buoyancy and this is equal to the weight of fluid displaced.

Viscous force:

This force is experienced by a body undergoing motion in a fluid. This force is proportional to the velocity of the object. This is also called drag force. Stokes law for drag experienced by a sphere is F=6πɳrv. An object falling through air keeps getting faster until the drag force equals the gravitational force and then it falls with a constant velocity called terminal velocity.

Momentum:

Momentum is the product of mass and velocity.

• P=mv
• It is a vector.
• SI unit is kgms^-1.

Impulse:

Impulse is the change in momentum of a body. It is often written as the product of force and time of action of force.

Units are the same as that of momentum and it is a vector

Newton’s laws of motion:

First law:

An object continues to stay at rest or to move with a constant velocity unless an external force acts on it.

Second law:

The rate of change of momentum of a body is directly proportional to the unbalanced force acting on the body and takes place in the same direction.

F = d_p/d_t

If the mass of system does not change with time,

F = m(dv/dt) = ma

E.g.: An elevator of mass m moves up with an acceleration a. Find the tension in cables.

T-mg=ma

T=m(g+a)

E.g.: Two masses are connected by a massless rope. The table is frictionless. Find the acceleration experienced by any one of the blocks.

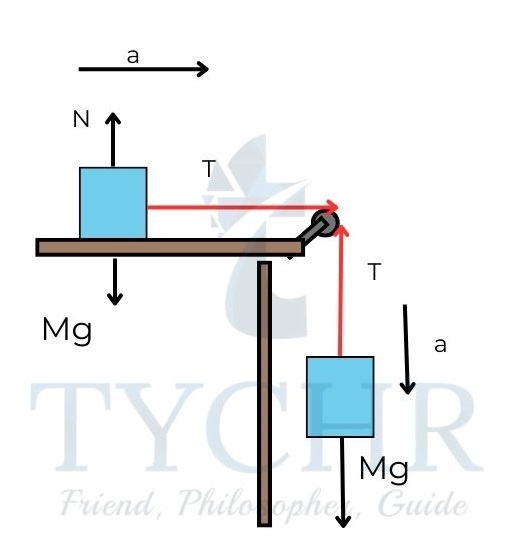
Applying Newton’s laws to the block on left
T=Ma

Applying Newton’s laws to the block on right
mg-T=ma
a=mg/(M+m)

Newton’s Third Law:

If a body A exerts a force on a body B, then the body B also exerts an equal and opposite force on A.

Law of conservation of energy:

The total momentum of a system remains constant if no external force acts on it.

Work, power and energy

Work:

Work done by a force is defined as the product of force and distance moved in the direction of force.

Work done = Force x Distance moved in the direction of force

W=FScos𝜃

Where 𝜃 is the angle between force and displacement.

Graphically, it is the area under force-displacement graph.

If the force and displacement are perpendicular to each other, then the work done by the force is zero.

It is a scalar and its SI unit is kgm²s^-2 or J.

E.g.: A force of 10N is applied on a block pulling it across a distance of 50m as shown in figure. Calculate the work done by the force.

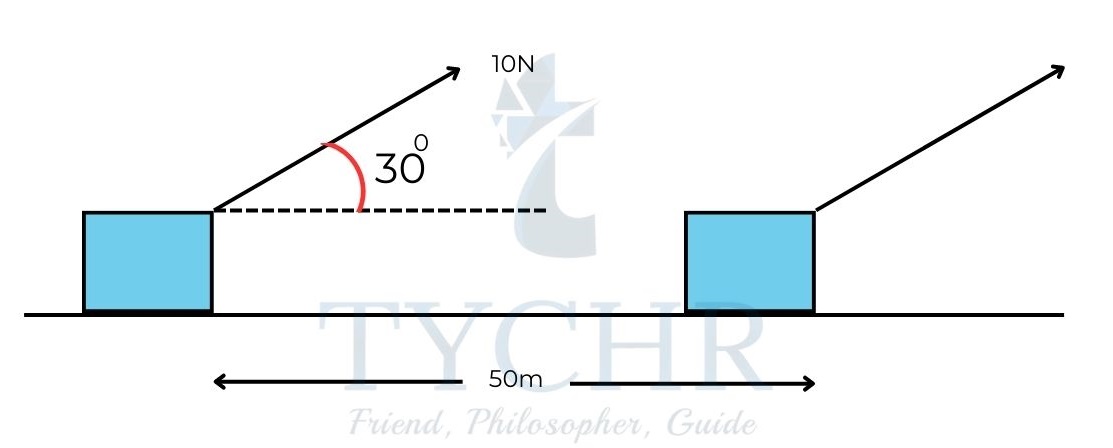
Work done W = FScosθ
W=10x50xcos(30˚)=433J

E.g.: When a car brakes, a decelerating force of 500N is produced and the car comes to rest in 25m. find the work done by frictional force.

Here, the force and displacement are in opposite direction.

W=500×25cos (180˚)=-12500J

Energy:

Energy is the quantity which enables a body to do work on another body.

Law of conservation of energy:

Energy can neither be created nor destroyed but can only be transferred from one form to another form.

Forms of energy:

Kinetic energy:

The energy possessed by a body by virtue of its motion. A body of mass ‘m’ moving with a velocity ‘v’ possesses a kinetic energy of 1/2(mv²).

Gravitational potential energy:

A body of mass ‘m’ resting at a height ‘h’ possesses a gravitational potential energy of mgh.

E.g.: A car of mass 1300kg accelerates from 12ms^-1 to 20ms^-1. Find the change in kinetic energy.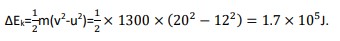

E.g.: A ball of mass 200g is thrown vertically up with a velocity of 2ms^-1. Find the maximum height reached by the ball.

Answer. The kinetic energy possessed by the body is completely converted into potential  energy by the time it reaches maximum height.

Loss in K.E = Gain in P.E
(1/2)mv² = mgh
h = v²/2g
h = 0.2m

Energy conversion:

Energy is converted in vehicles and machines with an efficiency.

Efficiency=useful work out/total energy in

Collisions:

In a collision, momentum and energy gets exchanged between objects.

Total momentum in a collision always remains constant.

Elastic collision:

In a completely elastic collision, total kinetic energy remains conserved.

• If the two bodies are of equal masses, then the velocities get exchanged.
• In case of unequal masses, the final velocities of masses are
  𝑣1 = ((𝑚₁ − 𝑚₂)/(𝑚₁ + 𝑚₂))𝑢₁ + (2𝑚_2/𝑚₁+ 𝑚₂)𝑢1

And the velocity of the second body is obtained by interchanging parameters of the 1st body with the 2nd body.

Same masses:

Different masses:

Collision in 2-D:

For a collision in 2-D, momentum components in two cartesian directions has to be conserved. Also, if the collision is elastic, kinetic energy has to be conserved. The above two constraints can be used to solve for the final velocities.

Inelastic collision:

In a perfectly inelastic collision, the two objects stick together and move with a common velocity. Momentum is conserved but there is a loss in kinetic energy.

The common velocity is given by 𝑣 = 𝑚₁𝑢/𝑚₁+𝑚₂ .

Find out the loss in kinetic energy due to inelasticity in terms of masses and initial velocities.

E.g.: A rail truck of mass 4500kg moving at a speed of 1.8 ms^-1 collides inelastically with a stationary truck of mass 1500kg. Find the velocity of the trucks after collision.

Answer. initial momentum is 4500×1.8 kgms^-1.

Final velocity is 4500×1.8 / (4500+1500) = 1.4ms^-1.

E.g.: Stone A of mass 0.5 kg travelling at 3.8 ms^-1 on a frozen pond collides with stationary stone B at rest. The stone B moves off with a velocity of 0.65 ms^-1 in the same direction. Calculate the velocity of stone A.

The initial momentum is 0.5 × 3.8 = 1.9 kgms^-1
The final momentum is 3.0 × 0.65 + 0.5v_a
1.9 = 3.0 × 0.65 + 0.5v_a
V_a=-0.1ms^-1

The final velocity of stone A is 0.1 kgms^-1 in the opposite direction to its original motion.

Power:

Power is the work done per unit time.

• It is a scalar.
• SI unit is Js^-1 or watt(W).

E.g.: A car of mass 1000 kg accelerates from rest to 100 kmh^–1 in 5 seconds. What is the average power of the car?

Answer. 100 kmh^-1 = 28 ms^-1.
The gain in KE of the car = 1/2mv² = 12× 1000 × 28² = 392 kJ
If the car does this in 5 s then power =work done/time =392/5 = 78.4 kW