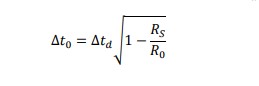Relativity Theory Notes
Check Out Our Results

OXFORD UNIVERSITY
(QS:3)

IMPERIAL COLLEGE
(QS:6)

CORNELL UNIVERSITY (QS:16)

45/45 (IBDP)
GEORGIA INSTITUTE

43/45 (IBDP)
KELLY SCHOOL
The beginnings of relativity
Reference frames:
A reference frame allows us to measure the kinematic parameters of a particle with reference to a fixed point. A reference usually consists of an origin, a cartesian set of axes. Inertial frames of reference are those which are at rest or move with a constant velocity.
Galilean transformations:
Moving between inertial reference frames and what they imply:
- Translation: Step from one reference frame to another – Position is relative.
- Rotation: The set of axes can be rotated to form another set – Direction is relative.
- Boost: One frame can move with a constant velocity relative to another – Velocity is relative.
If the distance between the origins of two reference frames S and S’ is X, then a position x in S is related to position x’ in S’ as x’=x-X.
If the velocity of S’ relative to S is v and origins coincide at t=0, then x’=x-vt.
The velocities also transform in a similar way U’=u-v.
Newton’s postulates:
Newton developed Galileo’s ideas further based on two postulates.
- Space and time are fixed and absolute.
- Two observers in two different inertial frames must make the same observations of the world.
Maxwell’s equations:
Maxwell developed four equations that describe all aspects of electromagnetism.
These equations predict the speed of light in vacuum. Also, the speed predicted in this manner does not depend on speed of observer, source or medium. So, the speed of light in all frames is the same. This also predicts the momentum of a photon to be h/𝜆.
Lorentz transformations
Postulates of special relativity by Einstein:
- The laws of physics are same in all inertial frames of reference.
- The speed of light in free space is same in all inertial frames of reference. Which means space and time are relative.
The Lorentz transformation:
There is an additional transformation that arises from the fact that time is absolute which is given by Δ𝑡 = Δ𝑡′.
The Lorentz factor is given by y 𝛾 = 1/√1−(𝑣2/𝑐2 .
Using this factor, Galilean equations are transformed as
𝑥′ = 𝛾(𝑥 − 𝑣𝑡) Δ𝑡′ = 𝛾Δ𝑡
Inverse Lorentz transformation of position is 𝑥 = 𝛾(𝑥′ + 𝑣𝑡)
Lorentz transformation of time is 𝑡′ = 𝛾(𝑡 −(𝑣/𝑐2)𝑥) and its inverse Lorentz transformation is 𝑡 = 𝛾(𝑡′ +(−𝑣/𝑐2)𝑥).
E.g.: Clocks in two frames S’ and S are adjusted so that when x=x’=0, t=t’=0. Frame S’ has a relative speed of 0.8c relative to S.
Event 1 occurs at x1=50m, t1=0.3𝜇s.
Event 2 occurs at x2=80m, t2=0.4𝜇s.
Find as measured in S’
i) the distance between x1 and x2.
ii) the time interval between t1 and t2.
Answer.
i) 𝛾 = 1.67
From the Lorentz transformation,
𝑥2′ − 𝑥1′ = 𝛾((𝑥2 − 𝑥1) − 𝑣(𝑡2 − 𝑡1)) = 10m
ii) 𝑡2′ − 𝑡1′ = 𝛾((𝑡2 − 𝑡1) −(𝑣/𝑐)((𝑥2 − 𝑥1)/𝑐)
𝑡2′ − 𝑡1′ = 30𝑛s
Velocity addition:
An object in frame A is moving with a velocity uA. Frame A is moving with a velocity v with respect to frame B with a velocity v. The velocity uB of the object as observed in frame B is given by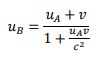
E.g.: Two rockets approach each other with speeds 0.9c and 0.8c. At what velocity will the rockets approach each other from the frame of reference of one of the rockets.
Answer.![]()
Here u=0.8c and v=-0.9c.
Substituting, we get u’=0.988c.
Invariant quantities:
These quantities are same in any inertial frame.
Spacetime interval:
Δs2 = (𝑐Δ𝑡)2 − Δ𝑥2
Rest mass:
The rest mass is the mass of a particle in frame which is at rest with respect to the particle.
Proper time:
The time interval between two events in a stationary frame (Δ𝑡0) is called proper time. It is measured in a frame where the two events occur at the same position. It is the shortest possible measured time interval between two events.
Proper length:
Proper length (𝐿0) is the length of an object measured from a frame which is at rest with respect to object. It is the longest possible measured length of the object.
Spacetime diagrams
Spacetime diagrams are useful for representing four-dimensional nature of spacetime using a graphical picture.
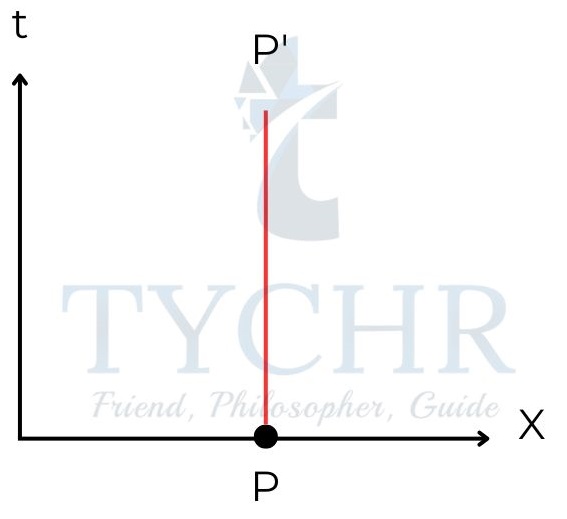
Position is plotted on X-axis with time on Y-axis. The plot of a particle is called worldline.
For a particle at rest with respect to the inertial frame of reference that is represented in the diagram, the world line (PP’) looks like the picture below.
For a particle Q moving with a constant velocity, the worldline looks like this.
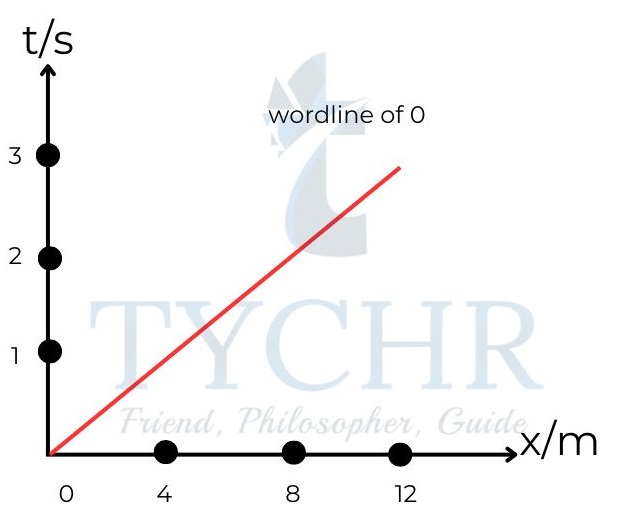
The angle between t and the worldline (𝜃) is given by:
𝑡𝑎𝑛𝜃 =𝑣 /c
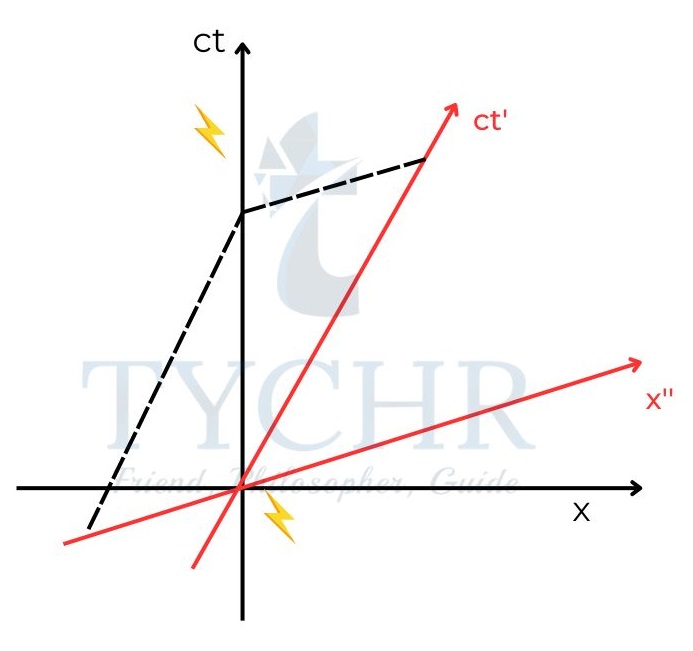
If a particle is observed that is moving at a velocity other than that of Q, its worldline can be represented in both frames as.
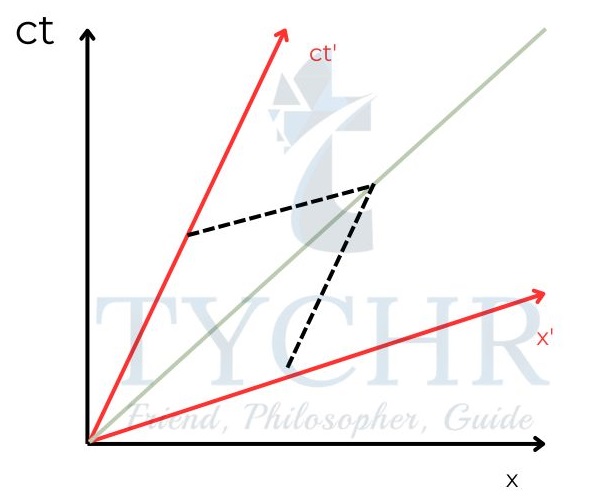
The green line represents a common world line for both frames (black for rest and red for moving frame). The ct’ axis represents the world line of the frame itself.
Simultaneity:
Using spacetime diagrams, it can be showed that simultaneous events occurring in one frame are not simultaneous in all frames.
Consider the example given below.
Two events occur simultaneously in an inertial frame. But they are not simultaneous in another frame. This is due to the fact that light travels with same speed irrespective of frame.
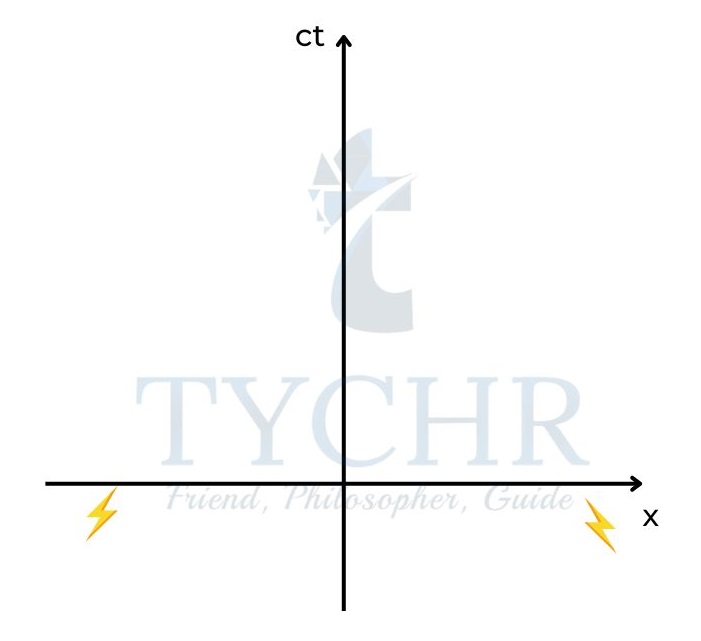
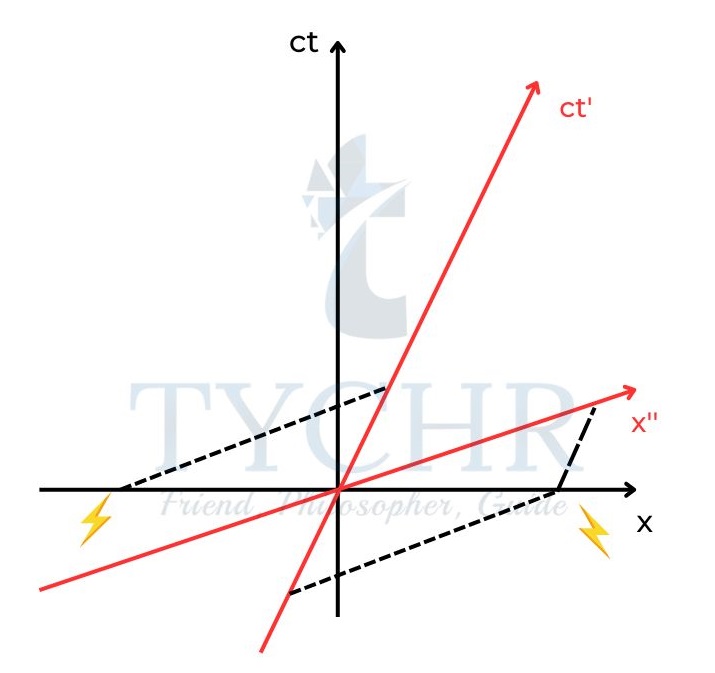
In a, the simultaneous events are represented with two lightening strikes. In b, it is clear that they are not simultaneous in another frame.
Time dilation:
Consider two events occurring at x=0 in S frame. If these events are observed in S’ frame, the time difference between the events is greater – the time has dilated in this frame.
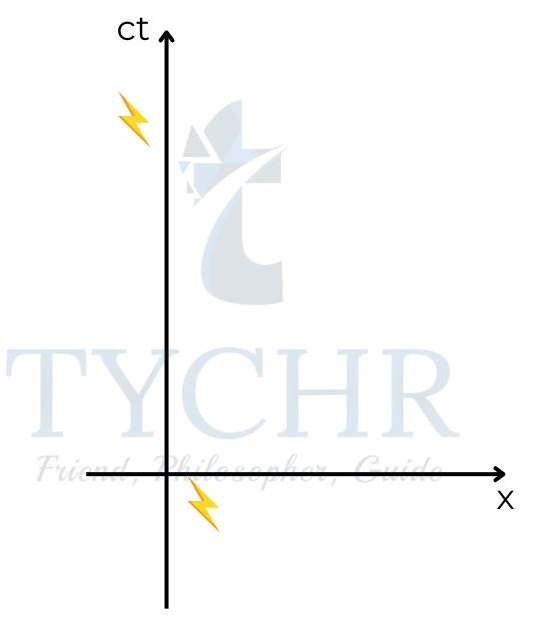
Muons are formed in atmosphere. Based on the decay constant for muons, it can be predicted that the number of muons reaching the surface of the earth are unnoticeable. But more muons than what is predicted reach the surface. Find a quantitative reason for this based on time dilation of muons due to their high speeds. |
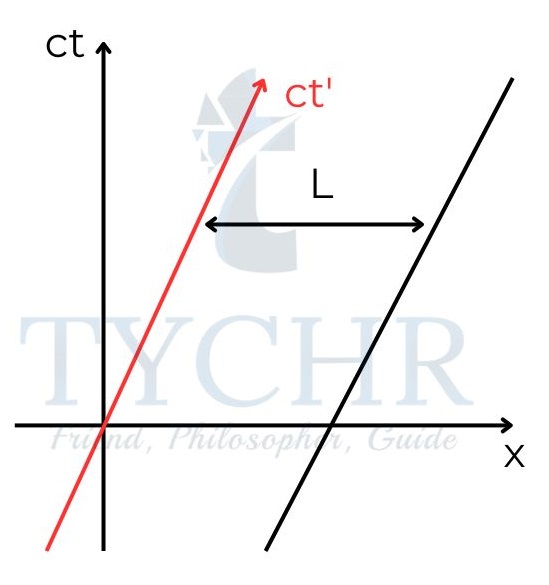
Length contraction:
Consider a rod whose length is being measured. The rod moves with a velocity equal to that of S’ frame. The length of rod measured from rest is L and L’ measured from the moving frame. L’ is greater than L. So, the length contracts when measured from a frame moving with respect to the object.
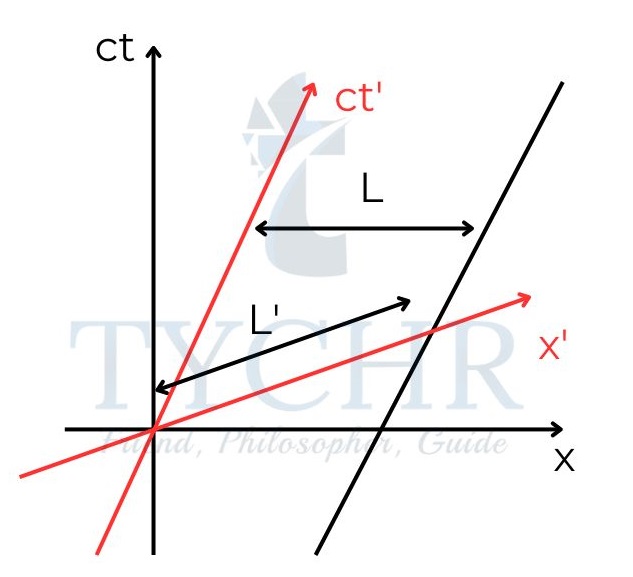
Consider an object travelling with a speed greater than that of light. Draw spacetime diagram for this. Draw the projection of the object on an axis for a frame travelling at a certain velocity. Use the time projections on this axis to show that it cannot travel faster than light. |
Relativistic mechanics
The rest mass of an object is m0. When this object moves with a velocity v, it possesses kinetic energy.
Energy:
The Newtonian mechanics predicts kinetic energy to be (1/2)𝑚𝑣2 and total energy to be (1/2)𝑚𝑣2+𝑚c2.
According to relativistic mechanics, the total energy of this object is 𝑚0𝛾𝑐2 and kinetic energy is 𝑚0(𝛾 − 1)𝑐2.
Momentum:
The momentum of the object according to relativistic mechanics is 𝑚0𝛾𝑣.
Energy-momentum formula:
Energy and momentum are related as 𝐸2 = 𝑝2𝑐2 + 𝑚02𝑐4
E.g.: Calculate the speed of an electron that is accelerated through a pd of 1MeV.
Answer. 𝐾. 𝐸 = 1𝑀𝑒𝑉
(𝛾 − 1)𝑚0𝑐2 = 1𝑀𝑒𝑉
Rest energy of an electron is 0.5MeV.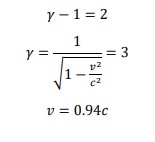
General relativity
The equivalence principle:
Einstein’s equivalence principle states that gravitational effects cannot be distinguished from inertial effects. The inertial mass and gravitational mass being equal are a consequence of this principle.
Gravitational red shift:
The frequency of light changes near mass. The decrease in frequency at a height h from a mass m is Δ𝑓/𝑓=𝑔Δℎ/𝑐2 . In accordance with the equivalence principle, the change is same for a body accelerating with g.
If the wave of light is regarded as a measure of time, then time passes slower near masses.
Bending of light near masses:
Light changes its path due to curvature of spacetime influenced by masses.
Gravitational lensing, where multiple images of a distant star can be observed around another star is a consequence of this effect.
Black holes:
For a mass M, the Schwarzschild radius is given by 𝑅𝑠 =2𝐺𝑀/𝑐2. If the whole mass falls within a sphere of this radius, then it forms a black hole. The change between two regimes r=RS is called event horizon. Events happening inside the event horizon do not affect events outside event horizon. The event horizon represents the surface inside which even light cannot escape.
The proper time interval (Δ𝑡0) for an observer at a distance R0 from a mass that has Schwarzschild radius RS is related to the time interval measured by a distant observer ( Δ𝑡d) is