Integral Calculus Notes
Statistics is a crucial branch of mathematics, providing tools for collecting, analyzing, and interpreting data. Within the IBDP Mathematics AA HL syllabus, statistical methods often rely on integral calculus for deeper understanding and more complex calculations. This study note explores the intersection of statistics and integral calculus, focusing on how integral calculus is applied in statistical concepts such as probability density functions, cumulative distribution functions, and expected values, all key components of the IB DP Mathematics AA HL curriculum. Mastering these connections is essential for success in the course.
By the end of this chapter, you will be familiar with:
- Integration as antidifferentiation
- Definite integrals
- Fundamental theorem of calculus
- Area under curves
- Boundary conditions
- Integration of various functions
- Integration by substitution
- Kinematics using integration
ANTIDERIVATIVE AND INDEFINITE INTEGRAL
By now we are familiar with differentiating common functions.
In this unit we carry out the process of differentiation in reverse. That is, we start with a given function, f(x) say, and ask what function or functions, F(x), would have f(x) as their derivative. This leads us to the concepts of an antiderivative and integration.
Consider the function f(x)=3x2+7x-2. Suppose we write its derivative as f(x), that is ![]() . We already know how to find this derivative by differentiating tem by term to obtain
. We already know how to find this derivative by differentiating tem by term to obtain ![]() Suppose now that we work back to front and ask ourselves which function or functions could possibly have 6x+7 as a derivative. Clearly, one answer to this question is the function 3x2+7x-2. We say f(x)=3x2+7x-2 is an antiderivative of f(x)=6x+7.
Suppose now that we work back to front and ask ourselves which function or functions could possibly have 6x+7 as a derivative. Clearly, one answer to this question is the function 3x2+7x-2. We say f(x)=3x2+7x-2 is an antiderivative of f(x)=6x+7.
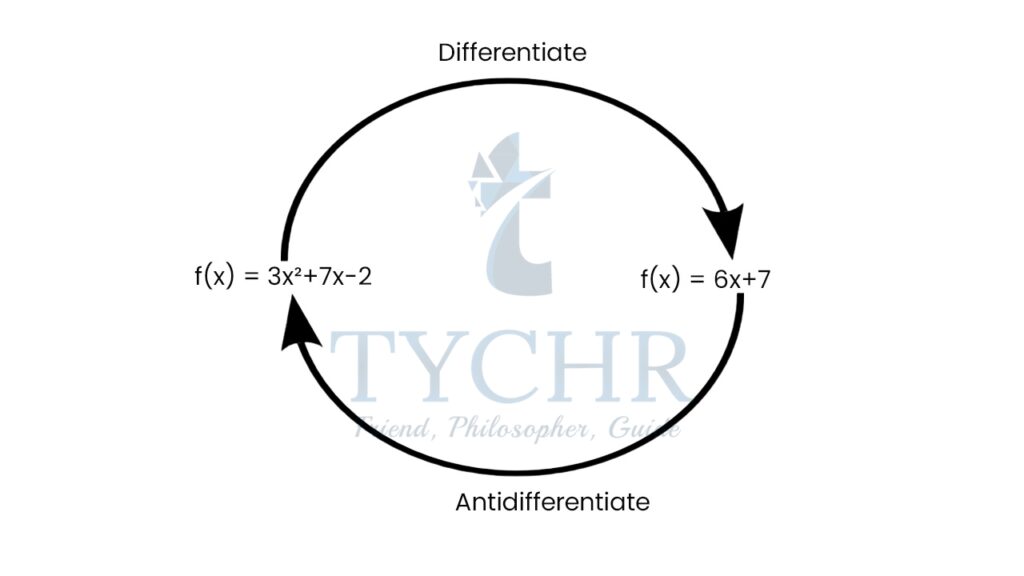
There are however other functions which have derivative 6x+7. Example
3x2+7x+3
3x2+7x
3x2+7x-12
The reason why all of these functions have the same derivative is that the constant term disappears during differentiation. So, all of these are antiderivatives of 6x+7.
Given any antiderivative of f(x), all others can be obtained by simply adding a different constant. In other words, if F(x) is an antiderivative of f(x), then so too is f(x)+C for any constant C.
If f'(x)=f(x) we write f(x)dx=f(x)+C
The expression ∫f(x)dx is called an indefinite integral.
Table of some common indefinite integrals:
f(x) | ∫f(x)dx=f(x)+C |
k (constant) | kx+C |
xn |
|
sin x | –cos x +C |
cos x | sin x +C |
ex | ex+C |
| ln x +C |
Rules for integration:
- Constant multiple rule
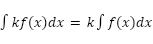
- Sum or difference rule
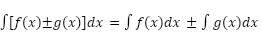
Ex. Find indefinite integrals of the following:
Solution:
INTEGRATION BY SUBSTITUTION
Integration by Substitution (also called “u-Substitution” or “The Reverse Chain Rule”) is a method to find an integral, but only when it can be set up in a special way.
Ex. ![]() We know that
We know that![]()
But here, we have another function inside the sine function.
Recall that, in chain rule of differentiation, we differentiate the inner function after differentiating the outer.
Let us multiply and divide the differentiation of the inner function in the intergral.![]() Now, we will put 3x+2=u
Now, we will put 3x+2=u
Differentiate the above equation:
3dx=du
Substitue the value of 3x+2 and 3dx in the integral![]()
Now, we can easily integrate-![]()
Putting the value of u:![]()
Using this simple substitution method, we have the following results:
f(x) | ∫f(x) |
(ax+b)n |
|
eax+b |
|
|
|
Ex. ![]() Let u=5x3+2
Let u=5x3+2
hence, du=15x2dx
We will need a factor of 15 in the integral![]() Substituting the value of u and du:
Substituting the value of u and du:![]() Now we can simply integrate:
Now we can simply integrate:![]() Substituing the value of u:
Substituing the value of u:![]()
Ex. ![]() Let sin(2x2)=u
Let sin(2x2)=u
hence, cos (2x2) 4xdx=du
We will need a factor of 4 in the integral![]() Substituting the value of u and du:
Substituting the value of u and du:![]() Now we can simply integrate:
Now we can simply integrate:![]()
![]() Substituing the value of u:
Substituing the value of u:![]()
AREA UNDER CURVE AND DEFINITE INTEGRAL
Consider that portion of the graph of y=f(x).
- Suppose f(x) lies entirely above the x axis. Clearly the area bounded by the graph A, and the x axis will depend on upon the value of x, A=A(x)

- Suppose we consider an additional contribution made to this area by moving a little to the right.
- Let this additional contribution be denoted by δA. Then δA is the change in area produced by increasing x by δx.
- Note then that δA=Ax+δx-A(x)
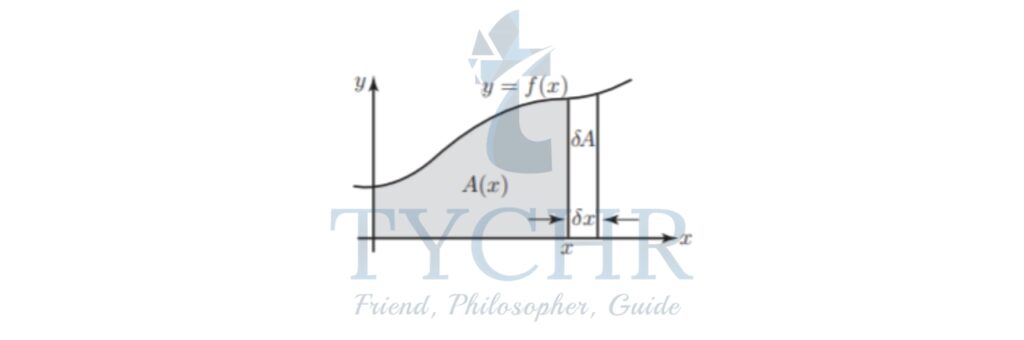
- Now, δA, can be approximated by assuming it has the form of a rectangle of height y=f(x) and width δx.
- That is δA≈f(x)δx or
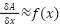
- In the limit as δx tends to zero we have
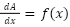
We can use the previous section to interpret this result.
Given that f(x) is the derivative of A(x) then, A(x) must be an antiderivative of f(x), i.e.
Ax=f(x)+C ①
We wrote f(x)+C for a whole family of functions all of which are antiderivatives when F(x) is. Now, we are looking for a specific antiderivative by choosing a specific value for
- C. This is obtained by noting that when x=0 the area bounded is zero, that is 0=F0+C, and this gives us a value for C, that is C=-F(0).
We can use this result as follows:
Given a function f(x), then the formula in Equation ① can tell us the area under the graph provided we can calculate an antiderivative F(x).
Suppose now we want to find the area under the graph between x=a and x=b as shown below:
The total area up to x=b is given, using Equation ①, by
A(b)=F(b)+C
The total area up to x=a is given, using Equation ①, by
A(a)=F(a)+C
And so, subtracting, the area between a and b is
A(b)-A(a)=F(b)-F(a)
Note how the C’s cancel out.
This area can be denoted by:![]()
This is what we call definite integral.
Properties of definite integral:
- Sum or difference:
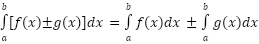
- Constant multiple:
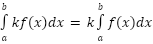
- Reverse interval:
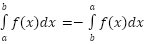
- Zero-length interval:
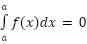
- Adding intervals:
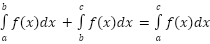
FUNDAMENTAL THEOREM OF CALCULUS
The fundamental theorem of calculus is a theorem that links the concept of differentiating a function with the concept of integrating a function.
The theorem has two versions:
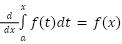 We start with a continuous function f and we define a new function for the area under the curve y=f(t)
We start with a continuous function f and we define a new function for the area under the curve y=f(t)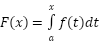 What this version of the theorem says is that the derivative of F is f. In other words, F is an antiderivative of f. Thus, the theorem relates differential and integral calculus, and tells us how we can find the area under a curve using antidifferentiation.
What this version of the theorem says is that the derivative of F is f. In other words, F is an antiderivative of f. Thus, the theorem relates differential and integral calculus, and tells us how we can find the area under a curve using antidifferentiation.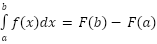 This version gives more direct instructions to finding the area under the curve y=f(x) between x=a and x=b. Simply find an antiderivative F and take F(b)-F(a).
This version gives more direct instructions to finding the area under the curve y=f(x) between x=a and x=b. Simply find an antiderivative F and take F(b)-F(a).
Ex. Calculate the area under the curve ![]() in the domain x=1 to x=2.
in the domain x=1 to x=2.
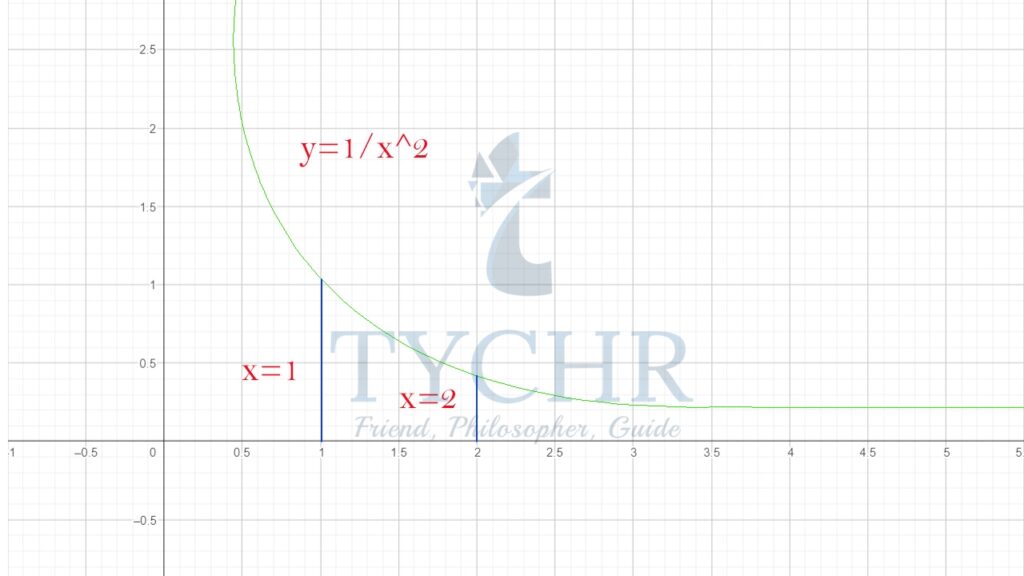
![]() Now,
Now, ![]() A=F2-F(1)
A=F2-F(1)
A=-12-(-1) ![]() units
units
Ex. Evaluate ![]() Using fundamental theorem of calculus:
Using fundamental theorem of calculus:![]()
Ex. Evaluate ![]()
![]()
![]()
![]()
![]()
![]()
Evaluating definite integrals by substitution:
Ex. Evaluate ![]() Putting 3x-2=u
Putting 3x-2=u
3dx=du
Since we are changing the variable, the limits will also change.
We have 3x-2=u
At x=2, u=4
At x=3, u=7
Now, the limits will become from u=4 to u=7 Putting the limits, u and du in the integral:![]()
![]()
![]()
![]()
AREA BETWEEN TWO CURVES
Recall that the area under the graph of y=f(x) between x=a and x=b, is given by:![]() Here, F(x) is the antiderivative of f(x)
Here, F(x) is the antiderivative of f(x)
If f(x) and g(x) are two functions, given that f(x)>g(x) in the interval [a,b], then the area between the curves y=f(x) and y=g(x) in this intevral is given by-![]() In terms of antiderivatives:
In terms of antiderivatives: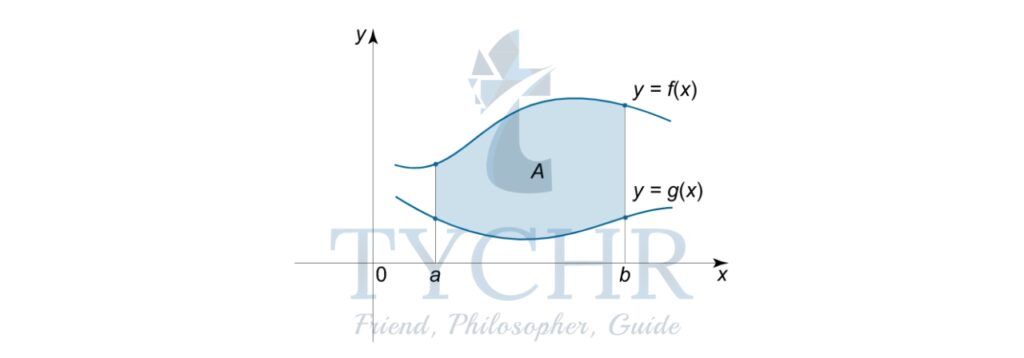
![]() Here, F(x) and G(x) are antiderivatives of the functions f(x) and g(x) respectively.
Here, F(x) and G(x) are antiderivatives of the functions f(x) and g(x) respectively.
Ex. Determine the area of the region enclosed by y=x2 and ![]()
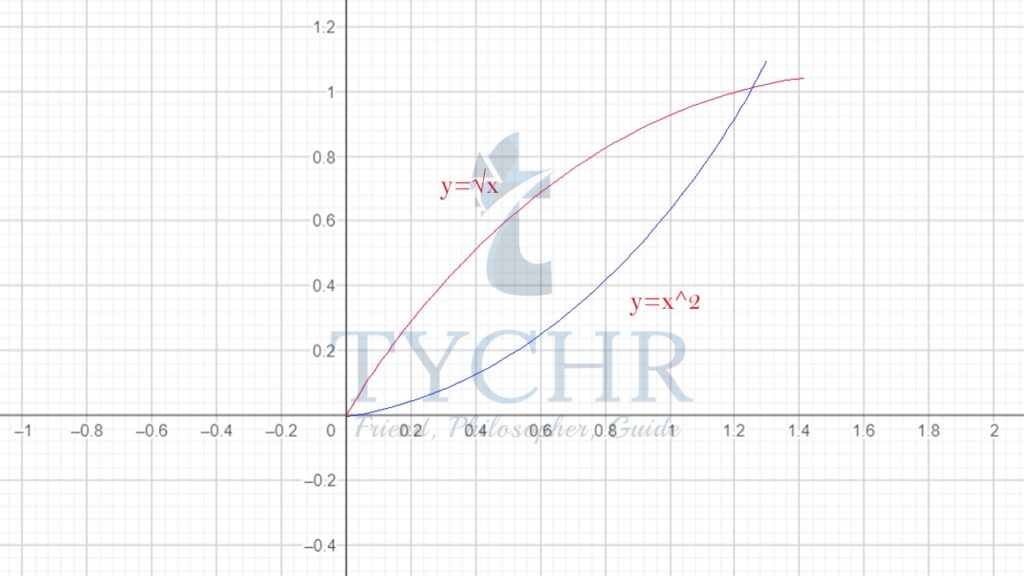
First lets plot the graph of the two functions.
The intersection of the two graphs is at 0,0 and (1,1)
The limits of the integration will be x=0 and x=1.![]()
![]()
![]()
![]() unit
unit
Ex. Find the area of the region in the first quadrant enclosed by the graphs of y2=x and y=x-2
Consider the graph:
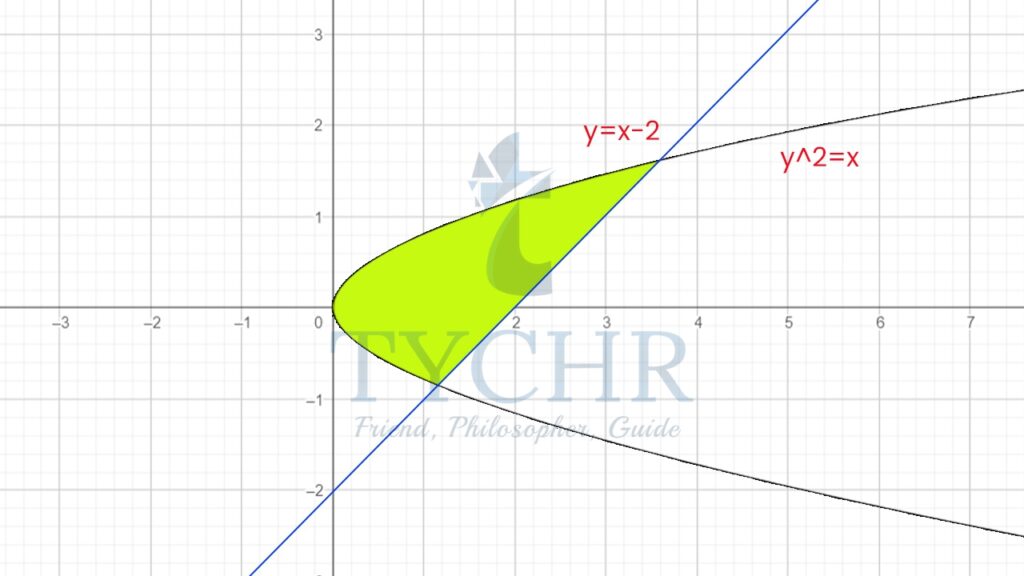
The graphs here, are along y-axis, so we will write the expressions, in terms of y:
x=y2
x=y+2
Now, we will determine the intersection of the two curves-
y2=y+2
(y+1)(y-2)=0
y=-1, y=2
Area =![]()
![]()
![]()
![]()
![]() units
units
KINEMATICS USING INTEGRATION
- If v is the velocity function for a particle moving along a straight line, then:
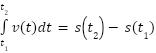 is the displacement from t1 to t2.
is the displacement from t1 to t2. 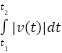 t gives the total distance travelled from t1 to t2.
t gives the total distance travelled from t1 to t2.- Similarly, the integration of acceleration function will give us the velocity function.
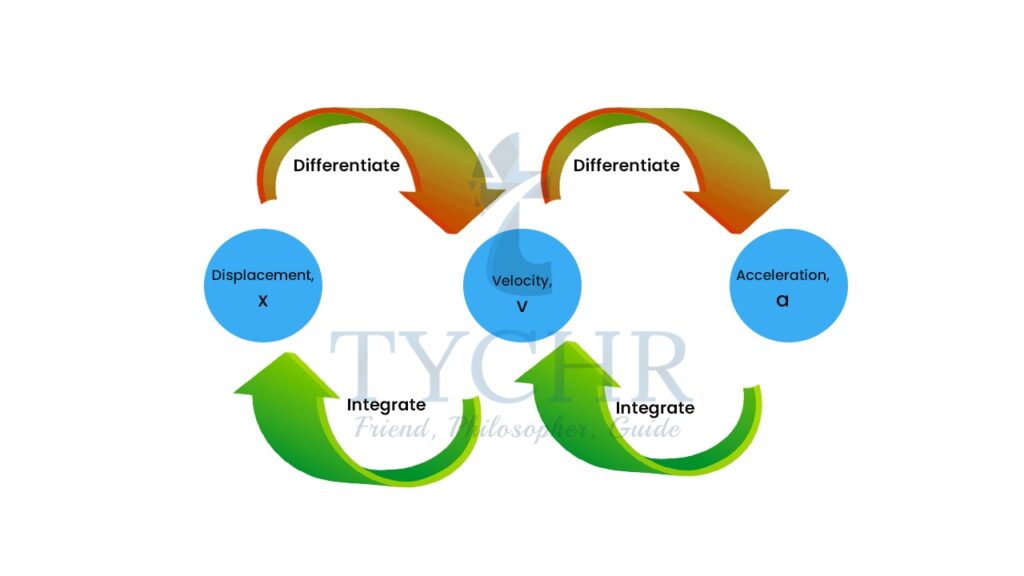
Ex. A particle P is moving along a straight line. The acceleration ams-1 from O can be written as a function of t
a=t+19
Suppose we know that when t=0, we have s=0 and when t=4 we have s=10. Find the displacement when t=10.
First we will find velocity by integrating the acceleration function:![]()
![]()
![]()
Now, we will integrate velocity to obtain the displacement:![]()
![]()
![]()
Now, putting t=0 and s=0
0=0+0+0+C2
C2=0
The displacement now becomes-![]()
Putting t=4 and s=10![]()
![]()
The displacement now becomes-![]()
Putting t=10
s=735 units
Integral calculus plays a vital role in advanced statistical analysis within the IB DP Mathematics AA HL syllabus. This study note has highlighted key applications in probability and distribution functions, and expected value calculations, all crucial for the course. Practice applying these techniques to various statistical problems is essential for solidifying your understanding. For personalized support in IB DP Mathematics AA HL, including the interplay of statistics and integral calculus and other syllabus topics, consider working with a tutor. TYCHR connects students with experienced IB Mathematics AA HL tutors who can provide tailored assistance. A strong grasp of these concepts will be instrumental in your success in IB DP Mathematics AA HL.

