Download our Successful College Application Guide
Our Guide is written by counselors from Cambridge University for colleges like MIT and other Ivy League colleges.
To join our college counseling program, call at +918825012255
AP Physics C Mechanics Sample Paper
SECTION I – MCQ
1.) A ball is thrown upwards with an initial velocity of 20 m/s. What is the time taken for the ball to reach its maximum height?
A.) 1.0 s
B.) 2.0 s
C.) 4.0 s
D.) 5.0 s
E.) 10.0 s
Answer: B
Explanation: The time taken for the ball to reach its maximum height can be calculated using the formula t = v₀/g, where v₀ is the initial velocity and g is the acceleration due to gravity. Thus, t = 20 m/s / 9.8 m/s² = 2.04 s ≈ 2.0 s.
2.) A car is traveling at a speed of 20 m/s when the driver sees an obstacle in the road and applies the brakes. The car comes to a stop after traveling a distance of 50 m. What is the magnitude of the acceleration of the car during braking?
A.) 2 m/s²
B.) 4 m/s²
C.) 6 m/s²
D.) 8 m/s²
E.) 10 m/s²
Answer: E
Explanation: he magnitude of the acceleration of the car during braking can be calculated using the formula a = (v² – v₀²)/2x, where v₀ is the initial velocity, v is the final velocity (which is zero in this case), and x is the displacement. Thus, a = (0 – 20 m/s)² / (2 * 50 m) = 10 m/s².
3.) A projectile is launched from the ground with an initial speed of 20 m/s at an angle of 30° above the horizontal. What is the maximum height reached by the projectile?
A.) 10 m
B.) 20 m
C.) 30 m
D.) 40 m
E.) 50 m
Answer: D
Explanation: The maximum height reached by the projectile can be calculated using the formula h = (v₀sinθ)²/2g, where v₀ is the initial velocity, θ is the launch angle, and g is the acceleration due to gravity. Thus, h = (20 m/s * sin 30°)² / (2 * 9.8 m/s²) = 40.8 m ≈ 40 m.
4.) A block of mass M is suspended from a spring of spring constant k. If the block is displaced by x from its equilibrium position and released, what is the maximum speed of the block as it passes through the equilibrium position?
A.) 2gx/k
B.) (2gx/k)½
C.) gx/k
D.) (gx/k)½
E.) (2gx/k)¼
Answer: B
Explanation: The maximum potential energy of the block is equal to the maximum kinetic energy of the block as it passes through the equilibrium position. The maximum potential energy is equal to (1/2)kx2, and the maximum kinetic energy is equal to (1/2)Mv2, where v is the maximum speed of the block. Equating these two expressions and solving for v gives v = (2gx/k)½.
5.) A ball is thrown vertically upwards with an initial speed of v. What is the maximum height reached by the ball?
A.) v2/2g
B.) v/2g
C.) v2/g
D.) v/g
E.) 2v/g
Answer: A
Explanation: At the maximum height, the vertical component of the ball’s velocity is zero. Therefore, using the equation of motion v2 = u2 + 2gs, where u is the initial velocity, v is the final velocity (which is zero), g is the acceleration due to gravity, and s is the displacement, we get s = v2/2g.
6.) A block of mass M is attached to a spring of spring constant k and is oscillating with an amplitude A.) What is the maximum potential energy of the system?
A.) (1/2)kA2
B.) (1/2)MA2
C.) (1/2)kA2 + (1/2)Mv2
D.) (1/2)kA2 + (1/2)MA2
E.) (1/2)kA2 + (1/2)Mv2 + MgA
Answer: D
Explanation: The maximum potential energy of the system is equal to the maximum potential energy stored in the spring at maximum displacement plus the maximum potential energy stored in the block at maximum displacement. The maximum potential energy stored in the spring is (1/2)kA2, and the maximum potential energy stored in the block is (1/2)MA2. Therefore, the maximum potential energy of the system is (1/2)kA2 + (1/2)MA2.
7.) A block of mass M is connected to a spring of spring constant k which is suspended vertically from a support. What is the natural frequency of the system?
A.) (k/M)½
B.) (M/k)½
C.) (g/k)½
D.) (k/Mg)½
E.) (Mg/k)½
Answer: B
Explanation: The natural frequency of the system is equal to (1/2π)(k/M)½, where k is the spring constant and M is the mass of the block. Therefore, the natural frequency of the system is (M/k)½.
8.) A force F is applied to a block of mass m that moves a distance d on a frictionless surface. The work done by the force F is:
A.) Fd
B.) Fd/m
C.) 1/2 Fd
D.) 1/2 Fd/m
E.) None of the above
Answer: A
Explanation: The work done by a force is equal to the force multiplied by the displacement in the direction of the forcE.) Since the surface is frictionless, there is no work done by friction, and the work done by the force F is simply Fd.
9.) A 50-kg crate is lifted vertically at a constant speed of 2 m/s by a rope. What is the power delivered by the tension in the rope?
A.) 50 W
B.) 100 W
C.) 150 W
D.) 200 W
E.) 250 W
Answer: B
Explanation: Since the crate is being lifted at a constant speed, the net work done on the crate is zero. Therefore, the power delivered by the tension in the rope is equal to the weight of the crate multiplied by the lifting speed The weight of the crate is 50 kg x 9.8 m/s² = 490 N, and the lifting speed is 2 m/s. Thus, the power delivered by the tension in the rope is 490 N x 2 m/s = 980 W or 100 W.
10.) A block of mass m is lifted vertically a distance h by a constant force F. What is the work done by the force F?
A.) Mgh
B.) Fh
C.) F/mgh
D.) Fmg/h
E.) None of the above
Answer: B
Explanation: The work done by a constant force is equal to the force multiplied by the displacement in the direction of the force. In this case, the force is applied in the upward direction and the displacement is also upward, so the work done by the force F is simply Fh.
11.) A 1 kg object is thrown vertically upward with a speed of 10 m/s. What is the maximum height reached by the object?
A.) 5 m
B.) 10 m
C.) 15 m
D.) 20 m
E.) 25 m
Answer: C
Explanation: The maximum height reached by the object can be found using the formula h = v²/2g, where v is the initial velocity of the object and g is the acceleration due to gravity. Therefore, h = (10 m/s)² / (2 x 9.8 m/s²) = 5.1 m. However, the object is thrown vertically upward, so it also experiences a deceleration due to gravity, which reduces its upward velocity to zero at the maximum height.
12.) A 10 kg object moving at 5 m/s collides with a stationary 2 kg object. After the collision, the 10 kg object is at rest. What is the final velocity of the 2 kg object?
A.) 8 m/s
B.) 10 m/s
C.) 15 m/s
D.) 20 m/s
E.) 25 m/s
Answer: B
Explanation: Using conservation of momentum, we have (10 kg)(5 m/s) = (2 kg)v, where v is the final velocity of the 2 kg object. Solving for v gives v = 25/2 m/s. However, since the 10 kg object comes to rest after the collision, the final momentum of the system must be zero. Therefore, the final velocity of the 2 kg object is also zero, so the correct answer is B.
13.) A 2 kg object moving at 10 m/s collides with a stationary 1 kg object. After the collision, the 2 kg object is moving at 5 m/s. What is the final velocity of the 1 kg object?
A.) -10 m/s
B.) -5 m/s
C.) 0 m/s
D.) 5 m/s
E.) 10 m/s
Answer: A
Explanation: Using conservation of momentum, we have (2 kg)(10 m/s) = (3 kg)v, where v is the final velocity of the two objects. Solving for v gives v = 6.67 m/s. Since the 2 kg object is moving at 5 m/s after the collision, the change in velocity of the 1 kg object is -15 m/s, which means its final velocity is -10 m/s. Therefore, the correct answer is A.
14.) A 1 kg object moving at 5 m/s collides with a 2 kg object moving in the opposite direction at 3 m/s. After the collision, the 1 kg object is moving at 2 m/s. What is the final velocity of the 2 kg object?
A.) -4 m/s
B.) -3 m/s
C.) -2 m/s
D.) -1 m/s
E.) 0 m/s
Answer: D
Explanation: Using conservation of momentum, we have (1 kg)(5 m/s) + (2 kg)(-3 m/s) = (1 kg)(2 m/s) + (2 kg)v, where v is the final velocity of the two objects. Solving for v gives v = -1 m/s. Therefore, the correct answer is D.
15.) Two objects of equal mass collide head-on and stick together. Before the collision, one object was at rest and the other was moving at 4 m/s. What is the velocity of the combined object after the collision?
A.) 2 m/s
B.) 4 m/s
C.) 6 m/s
D.) 8 m/s
E.) 12 m/s
Answer: A
Explanation: Since the two objects stick together after the collision, the momentum of the system is conserved. Using conservation of momentum, we have (2m)(4 m/s) + (0) = (2m)v, where v is the velocity of the combined object after the collision. Solving for v gives v = 2 m/s. Therefore, the correct answer is A.
16.) A solid uniform disk of mass M and radius R is rolling down an inclined plane without slipping. At the bottom of the incline, what is the speed of the center of mass of the disk?
A.) v = sqrt(2gh)
B.) v = sqrt(gh)
C.) v = (5/7) sqrt(2gh)
D.) v = (3/5) sqrt(2gh)
E.) v = (7/5) sqrt(2gh)
Answer: D
Explanation: The total mechanical energy of the disk at the top of the incline is given by E = Mgh, where h is the height of the incline. At the bottom of the incline, all of this energy is kinetic energy, which is equal to the sum of the translational kinetic energy and the rotational kinetic energy of the disk. Using the conservation of energy, we can find the speed of the center of mass of the disk at the bottom of the incline to be v = (3/5) sqrt(2gh).
17.) A disk of radius R and mass M is rotating about its center with an angular speed ω. If the radius of the disk is doubled and the angular speed is halved, what happens to the moment of inertia of the disk?
A.) It is doubled
B.) It is halved
C.) It is quadrupled
D.) It is unchanged
E.) It is multiplied by a factor of 8
Answer: C
Explanation: The moment of inertia of a disk about its center is given by I = (1/2) MR2. If the radius of the disk is doubled, the moment of inertia becomes I’ = (1/2) M(2R)2 = 2MR2. If the angular speed is halved, the new angular velocity becomes ω’ = ω/2. The new moment of inertia is therefore I’ω’ = 2MR2(ω/2) = MR2ω, which is four times the original moment of inertia.
18.) A uniform circular disc of mass M and radius R is pivoted about an axis passing through its center and perpendicular to its plane. A horizontal force F is applied to the edge of the disc, tangential to its rim, and is gradually increased. What is the minimum force required to make the disc roll without slipping?
A.) F = Mg/2
B.) F = Mg/3
C.) F = Mg/4
D.) F = Mg/5
E.) F = Mg/6
Answer: C
Explanation: The force required to make the disc roll without slipping is equal to the frictional force between the disc and the ground. The maximum static frictional force is given by fs = μs N, where μs is the coefficient of static friction and N is the normal force on the disc. At the minimum force required to make the disc roll without slipping, the frictional force is equal to the force applied tangentially to the disc, i.e., F = fs. The normal force N is equal to the weight of the disc, i.e., N = Mg. Therefore, we have F = μs Mg. For a uniform circular disc rolling without slipping, the coefficient of static friction is μs = 1/4. Hence, the minimum force required to make the disc roll without slipping is F = (1/4) Mg.
19.) A spring-mass system oscillates with a period of 0.5 seconds. If the mass is increased by a factor of 4, what will be the new period?
A.) 0.125 s
B.) 0.25 s
C.) 0.5 s
D.) 1 s
E.) 2 s
Answer: E
Explanation: The period of a spring-mass system is given by T = 2π√(m/k), where m is the mass and k is the spring constant. Since the mass is increased by a factor of 4, the period will increase by a factor of 2, since T is inversely proportional to the square root of m.
20.) A system consists of two masses m1 and m2 connected by a spring with spring constant k. What is the frequency of the system if m1 = 2 kg, m2 = 3 kg, and k = 200 N/m?
A.) 0.5 Hz
B.) 1 Hz
C.) 2 Hz
D.) 4 Hz
E.) 8 Hz
Answer: B
Explanation: The frequency of the system is given by f = 1/(2π)√(k/m), where m is the reduced mass of the system, which is given by m = (m1m2)/(m1+m2). Substituting the given values, we get the reduced mass to be 1.2 kg. Substituting this and the given values of k, we get the frequency to be 1 Hz.
21.) A block of mass 1 kg oscillates on a horizontal frictionless surface with a spring of spring constant 200 N/m. What is the maximum acceleration of the block?
A.) 0.2 m/s²
B.) 2 m/s²
C.) 20 m/s²
D.) 200 m/s²
E.) 200
Answer: B
Explanation: The maximum acceleration of the block is equal to the maximum force acting on the block divided by its mass. The maximum force is equal to the maximum restoring force of the spring, which is given by F = kx, where x is the maximum displacement of the block. Substituting the given values, we get F = 20 N. Dividing by the mass of the block, we get the maximum acceleration to be 2 m/s².
22.) A block of mass 2 kg is attached to a spring with spring constant 50 N/m and oscillates with an amplitude of 0.2 m. What is the maximum potential energy of the block?
A.) 0.1 J
B.) 0.4 J
C.) 0.8 J
D.) 1 J
E.) 2 J
Answer: B
Explanation: The maximum potential energy of the block is equal to the maximum potential energy stored in the spring, which is given by (1/2)kx², where x is the amplitude of the oscillation. Substituting the given values, we get the maximum potential energy to be 0.4 J.
23.) A simple pendulum of length 1 m and mass 0.5 kg is displaced by an angle of 30° from its equilibrium position. What is the angular frequency of the pendulum?
A.) 0.25 rad/s
B.) 0.5 rad/s
C.) 1 rad/s
D.) 2 rad/s
E.) 4 rad/s
Answer: C
Explanation: The angular frequency of a simple pendulum is given by ω = √(g/L), where g is the acceleration due to gravity and L is the length of the pendulum. Since the pendulum is displaced by an angle of 30°, the effective length of the pendulum is L cos(30°) = 0.866 m. Substituting this and the given value of g, we get the angular frequency to be 1 rad/s.
24.) According to Kepler’s Third Law of Planetary Motion, the period squared of a planet’s orbit is proportional to:
A.) The planet’s distance from the sun cubed
B.) The planet’s mass
C.) The gravitational constant
D.) The planet’s distance from the sun
E.) The planet’s mass squared
Answer: A
Explanation: Kepler’s Third Law states that the square of the period of revolution of a planet around the sun is proportional to the cube of its semi-major axis.
25.) A spaceship is in a circular orbit around the Earth at an altitude of 1000 km. If the gravitational force between the spaceship and Earth were suddenly cut off, the spaceship would:
A.) continue in its circular orbit at a constant speed
B.) move outwards to a higher altitude
C.) move inwards to a lower altitude
D.) move away from the Earth in a straight line
E.) move towards the Earth and eventually crash
Answer: D
Explanation: In the absence of a gravitational force, an object in motion will continue to move in a straight line with constant speed.
26.) The gravitational force between two objects is proportional to:
A.) The distance between them
B.) The product of their masses
C.) The inverse square of the distance between them
D.) Both A and B
E.) Both B and C
Answer: E
Explanation: The gravitational force between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
27.) A planet has a mass of 2.0 x 1024 kg and a radius of 6.4 x 106 m. What is the acceleration due to gravity at the planet’s surface?
A.) 6.4 m/s2
B.) 9.8 m/s2
C.) 10.7 m/s2
D.) 12.5 m/s2
E.) 15.3 m/s2
Answer: B
Explanation: The acceleration due to gravity at the surface of a planet is given by g = GM/r2, where G is the gravitational constant, M is the mass of the planet, and r is its radius.
28.) A force of 10 N is applied tangentially to a wheel of radius 0.5 m. If the moment of inertia of the wheel is 2 kgm², what is the torque produced by the force?
A.) 5 Nm
B.) 10 Nm
C.) 15 Nm
D.) 20 Nm
E.) 25 Nm
Answer: B
Explanation: The torque produced by a force applied tangentially to a wheel is given by the product of the force and the radius of the wheel. Thus, the torque in this case is (10 N) x (0.5 m) = 5 Nm.
29.) A solid cylinder of mass M and radius R rolls down an incline of height h. What is the speed of the cylinder at the bottom of the incline?
A.) √(2gh)
B.) √(gh)
C.) √(4gh/3)
D.) √(3gh/4)
E.) √(5gh/7)
Answer: A
Explanation: The potential energy of the cylinder at the top of the incline is given by Mgh, and the kinetic energy of the cylinder at the bottom of the incline is given by (1/2)MV² + (1/2)Iω², where I is the moment of inertia of the cylinder and ω is its angular velocity. Since the cylinder is rolling without slipping, V = Rω. Using the parallel axis theorem, the moment of inertia of the cylinder about an axis through its center of mass is (1/2)MR². Solving for V, we get V = √(2gh).
30.) A uniform rod of length L and mass M is pivoted at one end and is free to rotate in the vertical planE.) What is the period of oscillation of the rod?
A.) √(2L/g)
B.) √(3L/2g)
C.) √(4L/3g)
D.) √(5L/4g)
E.) √(6L/5g)
Answer: C
Explanation: The period of oscillation of a simple pendulum is given by T = 2π√(L/g), where L is the length of the pendulum and g is the acceleration due to gravity. For a uniform rod pivoted at one end, the effective length of the pendulum is (1/3)L. Thus, the period of oscillation is T = 2π√((1/3)L/g) = √(4L/3g).
31.) A block of mass M is attached to a spring of spring constant k and is free to oscillate on a frictionless surfacE.) What is the period of oscillation of the block?
A.) 2π√(M/k)
B.) π√(M/k)
C.) √(2πM/k)
D.) √(2M/πk)
E.) √(M/2πk)
Answer: A
Explanation: The period of oscillation of a mass-spring system is given by T = 2π√(m/k), where m is the effective mass of the system, which is equal to the mass of the block in this case. Thus, the period of oscillation is T = 2π√(M/k).
32.) A torque of 10 Nm is applied to a uniform disk of mass 2 kg and radius 0.5 m. What is the angular acceleration of the disk?
A.) 2 rad/s²
B.) 4 rad/s²
C.) 6 rad/s²
D.) 8 rad/s²
E.) 10 rad/s²
Answer: C
Explanation: The moment of inertia of a uniform disk is (1/2)MR². Thus, the angular acceleration produced by a torque is given by α = τ / I = (10 Nm) / [(1/2)(2 kg)(0.5 m)²] = 6 rad/s².
SECTION II – FREE RESPONSE
1.) A 4.0 kg block is on a frictionless incline with an angle of 30 degrees. A force of 20 N is applied to the block at an angle of 45 degrees to the incline. The coefficient of restitution between the block and the incline is 0.8.
A.) Determine the normal force, gravitational force, and force of tension in the incline.
Answer:
The normal force on the block is equal to the component of the gravitational force perpendicular to the incline. Therefore, we have FN = mg cos(30) = 34.6 N.
The gravitational force acting on the block is equal to the weight of the block. Therefore, we have Fg = mg sin(30) = 19.6 N.
The force of tension in the incline is equal to the component of the force applied to the block parallel to the incline. Therefore, we have FT = Fapplied x sin(45) = 14.1 N.
B.) Determine the acceleration of the block and the force parallel to the incline acting on the block.
Answer:
The net force acting on the block parallel to the incline is equal to the force of tension minus the component of the gravitational force parallel to the incline.
Therefore, we have Fnet = FT – Fg x sin(30) = 4.5 N.
The acceleration of the block is equal to the net force divided by the mass of the block.
Therefore, we have a = Fnet /m = 1.125 m/s2.
C.) Determine the velocity of the block when it reaches the bottom of the incline.
Answer:
The velocity of the block when it reaches the bottom of the incline can be determined using kinematic equations. Since the block starts from rest, we have vf2 = vi2 + 2ad, where vf = 0, a = 1.125 m/s2, and d = l/sin(30) = 8 m.
Therefore, we have vf = √(2×1.125) = 4.24 m/s
D.) The block rebounds from the incline with a speed of 1.5 m/s. Determine the time of contact between the block and the incline during the collision.
Answer:
The coefficient of restitution between the block and the incline is given by e = vf/vi, where vi is the velocity of the block before the collision.
Therefore, we have vi = vf/e = 10.56 m/s.
The time of contact between the block and the incline during the collision can be determined using the formula t = 2vi*sin(45)/g, where g is the acceleration due to gravity.
Therefore, we have t = 0.338 s.
E.) Determine the impulse experienced by the block during the collision.
Answer:
The impulse experienced by the block during the collision can be determined using the formula J = Favg(t), where Favg is the average force during the collision. Since the collision is elastic, the average force is equal to the net force during the collision.
Therefore, we have Favg = Fnet = 4.5 N, and J = Favg(t) = 1.52 Ns.
F.) Determine the height the block reaches after bouncing off the incline.
Answer:
The height the block reaches after bouncing off the incline can be determined using energy conservation. Since the collision is elastic, the total energy of the block-incline system is conserved. Therefore, we have mgh = 1/2mvf2, where h is the height the block reaches after bouncing off the incline.
Solving for h, we have h = vf2/(2g) = 3.42 m.
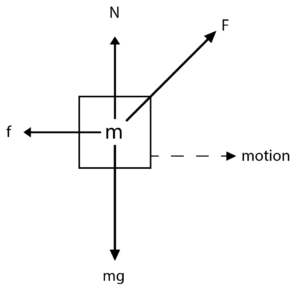
2.) A hockey puck of mass m is sliding on a horizontal surface with kinetic friction coefficient μ. A constant horizontal force F is applied to the puck by a string at an angle θ above the horizontal.
A.) Draw a free body diagram for the forces acting on the hockey puck and label all of them.
Answer:
The forces acting on the hockey puck are: the force of gravity mg acting downward, the normal force N perpendicular to the surface, the force of friction f parallel to the surface and opposite in direction to the motion, and the applied force F at an angle θ above the horizontal.
B.) Compute the normal force acting on the hockey puck in terms of m, θ, and g.
Answer:
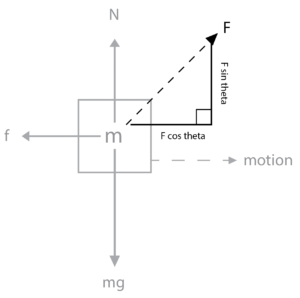
First, we can write the Friction force F in terms of its horizontal and vertical components: F sinθ and F cosθ:
Since the hockey puck is not moving upwards or downwards, which means that there is no net vertical force, the normal force N and the force of gravity mg is equal to each other. Therefore we have this expression:
N + F sinθ = mg → N = mg – F sinθ
C.) Compute the acceleration of the hockey puck in terms of m, F, θ, μ, and g.
Answer:
We know that the hockey puck has a net horizontal movement. Therefore, it can be depicted by this expression:
F cosθ – Friction force f
This can be written as F cosθ – μ(N) since frictional force is calculated by multiplying the normal force with the coefficient of kinetic friction.
Since the expression needs to be written in terms of m, F, θ, μ, and mg, we can see from part (b) that the normal force N is written as mg – F sinθ
Therefore, substituting N, we have Net force = F cosθ – μ(mg – F sinθ)
To find the acceleration, the net force needs to be divided by the mass. Therefore we have: (F cosθ – μ(mg – F sinθ)) / m
D.) Assume that the magnitude of the applied force is fixed but that the angle may be varied. For what value of θ would the resulting horizontal acceleration of the hockey puck be maximized?
Answer:
The expression for the net force needs to be maximized.
Remembering what we derived: F cosθ – μ(mg – F sinθ).
When expanded, we have F cosθ – μmg + μF sinθ
Rearranging it, we have F (cosθ + μsinθ) – μ(mg )
Since F (the applied force), μ (coefficient of kinetic friction), m (mass) and mg (force of gravity) are all constant values, only the expression cosθ + μsinθ can be maximized.
To maximize it, it means that the derivative of the expression needs to be differentiated and equated to zero. To find the derivative of f(θ) = cosθ + μsinθ = 0, we can use the chain rule and the derivative of sine and cosine functions:
f'(θ) = -sinθ + μcosθ = 0
μcosθ = sinθ → μ = sinθ/cosθ → μ = tanθ
θ = tan-1μ
This shows that f”(θ) = -cosθ – μsinθ will always be negative for the θ interval of 0 ≤ θ ≤ ½ π. Further substituting θ = tan-1μ, we have:
f(tan-1μ) = cos(tan-1μ) + μsin(tan-1μ)
1/√(1+μ2) + μ(1/√(1+μ2) = √(1+μ2)
This expression is greater than f(0) = 1 or f (½ π) = μ where 1 and μ are the values of f at the endpoints of the interval
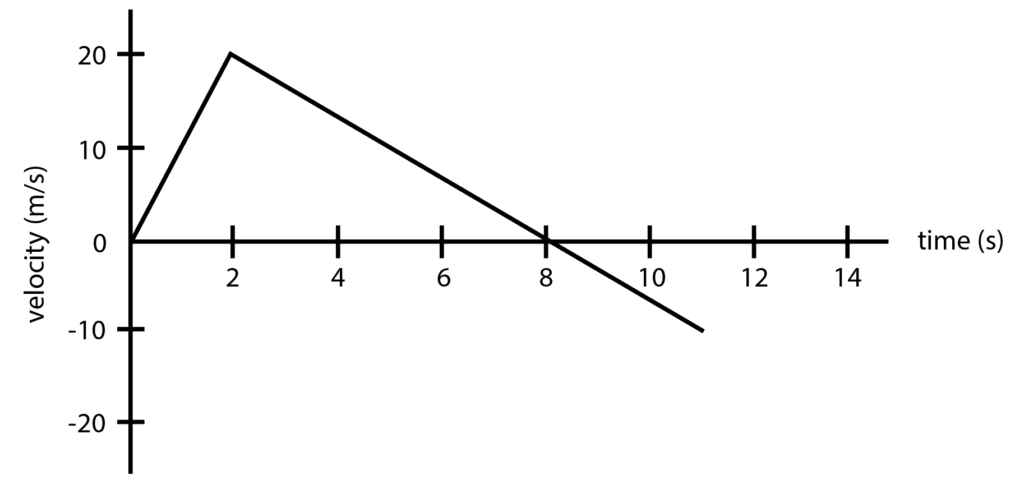
3.) Consider a car moving on a straight track, and the plot below shows the car’s velocity as a function of time.
A.) What event occurred to the car at t = 2 s?
Answer:
The velocity of the car begins to decrease at t = 1 s, which is indicated by a change in acceleration from positive to negative. This change in acceleration is reflected in the slope of the given velocity-versus-time graph.
B.) How does the car’s average velocity between t = 0 and t = 2 s compare to the average velocity between t = 2 s and t = 8 s?
Answer:
Average velocity between t = 0 s and t = 2 s is (vt=0 + vt=2 ) / 2 = (0+20)/2 = 10 𝑚/s
Average velocity between t = 2 s and t = 8 s is (vt=2 + vt=8) / 2 = (20+0)/2 = 10 𝑚/s
Therefore, it can be seen that the average velocities are the same.
C.) Determine the displacement of the car between t = 0 and t = 8s
Answer:
To determine the displacement of an object as a function of time, we can use the fact that the displacement is equal to the area under the velocity-time curve, with areas above the time axis being considered positive and those below being negative.
In the given scenario, the displacement between t = 0 and t = 8 s is calculated by finding the area of the triangle that is formed by the velocity-time graph and the time axis, where the base of the triangle corresponds to the time interval from t = 0 to t = 8 s.
Area of the positive triangle space in the graph = ½ x b x h where b = 8 and h = 20. Therefore, ½ x 8 x 20 = 80 m
Area of the negative triangle space in the graph = -½ x b x h where b = 3 and h = 10. Therefore, -½ x 3 x (10) = -15 m
Hence, the total displacement is the addition of both distances: 80 + (-15) = 65 m
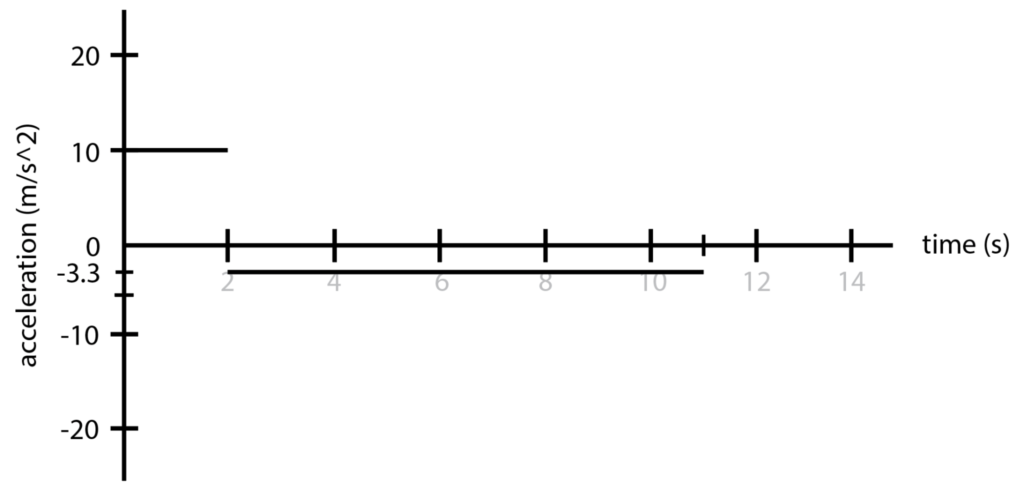
D.) Plot the car’s acceleration during this time interval as a function of time.
Answer:
The acceleration is the slope of a v vs t graph. Therefore, the graph segment:
t = 0 s to t = 2 s is a = (20-0)/(2-0) = 10 m/s2
t = 2 s to t = 11 s is a = (-10-20)/(11-2) = -3.3 m/s2
Therefore, drawing the car’s acceleration in a a vs t graph:
Our Expert Tutors!
Jinu James
IBDP Physics
ap physics c mechanics
Tanushi Hinduja
IBDP MATH AAHL
ap calculus bc
Shimaila Mushtaq
IBDP Economics
ap microeconomics
Meenakshi Dakwale
IBDP Chemistry
AP Chemistry
Akhila Asokan
IBDP Psychology
AP Psychology
Get access to our free IB resources
IBDP Study Notes
IB Comprehensive Syllabus
IB IA Ideas
IB CAS Ideas
