Table of Contents
IGCSE Math is a secondary school qualification that is recognized globally and is designed to provide a strong foundation in mathematics. The curriculum covers a wide range of topics such as algebra, geometry, trigonometry, statistics, and calculus. It is designed to develop logical and critical thinking skills, problem-solving abilities, and a strong understanding of mathematical concepts.
IGCSE Math is a two-year program that is typically taken by students in grades 9 and 10. It is offered by the University of Cambridge International Examinations (CIE) and is widely accepted by universities and employers around the world. The course is divided into two levels: Core and Extended. The Core level covers the essential mathematical concepts that are needed for everyday life, while the Extended level provides a more in-depth understanding of the subject.
Assessment is based on a combination of written exams and coursework. Students who successfully complete the program are awarded a certificate of achievement, which is recognized by universities and employers around the world. Overall, IGCSE Math is an excellent qualification for students who wish to pursue higher education in mathematics or a related field, or for those who simply want to develop their mathematical skills and knowledge.
Paper Pattern:
Paper 1:
| Duration | 1 hour |
| Total Marks | 56 |
| Type of Questions | Short Answer Questions |
| Calculator Usage | Allowed(Only certain types of scientific calculators allowed) |
Paper 3:
| Duration | 2 hours |
| Total Marks | 104 |
| Type of Questions | Structured Questions |
| Calculator Usage | Allowed(Only certain types of scientific calculators allowed) |
Core 1: Number
In this unit, students delve into fundamental concepts of numbers as also outlined in the comprehensive IGCSE Syllabus for Grade 9 Maths, including operations, properties, and number patterns.
| Subtopic Number | Subtopic | IGCSE Points to understand |
| C1.1 | Identify and use natural numbers, integers (positive, negative and zero), prime numbers, square and cube numbers, common factors and common multiples, rational and irrational numbers (e.g. π, 2 ), real numbers, reciprocals. | Natural numbers: Natural numbers are whole numbers greater than zero. They are used to count things.
Integers: Integers are whole numbers (positive, negative, or zero) and are used to represent values such as gains and losses, temperatures, and elevations. Prime numbers: Prime numbers are numbers that have only two factors, one and itself. Examples include 2, 3, 5, 7, 11, 13, 17, 19, and so on. Common factors and common multiples: Common factors are numbers that divide evenly into two or more numbers. Common multiples are numbers that are multiples of two or more numbers. Rational and irrational numbers: Rational numbers are numbers that can be expressed as a ratio of two integers, while irrational numbers cannot. Examples of irrational numbers include pi (π) and the square root of 2. Real numbers: Real numbers are all the numbers on the number line, including rational, irrational, positive, negative, and zero. Reciprocals: Reciprocals are numbers that, when multiplied together, result in 1. For example, the reciprocal of 4 is 1/4, and the reciprocal of 1/2 is 2. |
| C1.2 | Understand notation of Venn diagrams.
Definition of sets e.g. A = {x: x is a natural number} B = {a, b, c, …} |
Notation of Venn diagrams: Venn diagrams are visual representations of sets using overlapping circles or rectangles. They can be used to show relationships between sets and to solve problems involving set operations such as union, intersection, and complement.
Definition of sets: A set is a collection of distinct objects or elements. Sets can be defined by listing the elements between braces or by using set-builder notation. For example, the set A = {1, 2, 3, 4} contains the elements 1, 2, 3, and 4, while the set B = {x | x is a positive integer less than 5} contains the same elements but is defined using set-builder notation. The set C = {a, b, c} contains the elements a, b, and c. |
| C1.3 | Calculate with squares, square roots, cubes and cube roots and other powers and roots of numbers | Squares: Squaring a number means multiplying it by itself. For example, the square of 5 is 5×5 = 25.
Square roots: The square root of a number is the value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because 5×5 = 25. Cubes: Cubing a number means multiplying it by itself three times. For example, the cube of 3 is 3x3x3 = 27. Cube roots: The cube root of a number is the value that, when multiplied by itself three times, gives the original number. For example, the cube root of 27 is 3, because 3x3x3 = 27. Other powers and roots: In addition to squares and cubes, numbers can be raised to any power (e.g. to the fourth power, to the fifth power, etc.) and can have any root (e.g. the fourth root, the fifth root, etc.). Calculating with powers and roots involves using the appropriate formulas or rules for each type of operation. |
| C1.4 | Use directed numbers in practical situations. | Directed numbers are positive or negative numbers used to indicate movement or direction. They are used in practical situations, such as measuring temperatures below zero or calculating distances between two points in opposite directions. Multiple operations such as addition, subtraction, ordering, multiplication and division can be performed on these numbers. |
| C1.5 | Use the language and notation of simple vulgar and decimal fractions and percentages in appropriate contexts. | Fractions: A fraction is a way of expressing a part of a whole. The top number is called the numerator, and the bottom number is called the denominator. Fractions can be written as vulgar fractions (e.g., 2/3) or as decimals (e.g., 0.5 or 0.75).
Decimals: A decimal is a way of expressing a number that is not a whole number. It is written with a decimal point and digits after the point. Decimals can be used to represent parts of a whole or to compare quantities. Percentages: A percentage is a way of expressing a fraction or a decimal as a number out of 100. Percentages can be used to compare quantities, to express a part of a whole, or to show a change over time. Conversion between fractions, decimals, and percentages: Understanding how to convert between fractions, decimals, and percentages is important for solving problems and working with data. For example, knowing that 50% is the same as 0.5 or 1/2 can be useful when calculating discounts or working with data in graphs. Applications in real-life situations: The language and notation of fractions, decimals, and percentages are used in many real-life situations, such as cooking recipes, financial calculations, and data analysis. Being able to understand and use these concepts is important for making informed decisions and solving problems in everyday life. |
| C1.6 | Order quantities by magnitude and demonstrate familiarity with the symbols =, ≠, <, > , ⩾, ⩽ . | Magnitude refers to the size or scale of a quantity or number. This subtopic involves understanding the relative size of numbers and using symbols to compare them.
The symbols used to compare quantities are:
Understanding how to order quantities by magnitude and use these symbols is important for many mathematical operations, including solving equations and inequalities. |
| C1.7 | Understand the meaning of indices (fractional, negative and zero) and use the rules of indices. Use the standard form A × 10n where n is a positive or negative integer, and 1 ⩽ A < 10. | Understand the meaning of indices (fractional, negative and zero): This subtopic involves understanding the meaning of indices and how to work with fractional, negative, and zero indices. This includes understanding how to convert between different forms of an expression involving indices, as well as understanding the properties of indices such as the product and quotient rules.
Use the rules of indices: This subtopic involves using the rules of indices to simplify expressions involving powers and roots, and to solve equations involving indices. This includes understanding how to use the product, quotient, power, and root rules of indices, as well as understanding how to apply these rules in various contexts. Use the standard form A × 10n where n is a positive or negative integer, and 1 ⩽ A < 10: This subtopic involves understanding how to write numbers in standard form and how to perform calculations involving numbers in standard form. This includes understanding the meaning of the terms “mantissa” and “exponent,” as well as understanding how to convert between standard form and ordinary decimal form. |
| C1.8 | Use the four rules for calculations with whole numbers, decimals and fractions (including mixed numbers and improper fractions), including correct ordering of operations and use of brackets | Four rules of calculations: Addition, subtraction, multiplication, and division are the four basic arithmetic operations. These rules apply to whole numbers, decimals, and fractions, including mixed numbers and improper fractions.
Correct ordering of operations: To solve a mathematical problem that involves more than one operation, it is important to perform the operations in the correct order. The order of operations is usually remembered by the acronym PEMDAS, which stands for Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right). Use of brackets: Brackets are used in mathematical expressions to indicate that the operations inside the brackets should be performed first. This can help to avoid confusion and ensure that the correct order of operations is followed. |
| C1.9 | Make estimates of numbers, quantities and lengths, give approximations to specified numbers of significant figures and decimal places and round off answers to reasonable accuracy in the context of a given problem | Estimating numbers: Estimation is the process of making an educated guess about the value of a number, quantity or length. It is useful when working with large or complex numbers or when a precise answer is not needed.
Approximating to specified numbers of significant figures and decimal places: This involves rounding a number to a certain number of significant figures or decimal places. This is important in science, engineering and other technical fields where precise measurements are required. Rounding off answers to reasonable accuracy: This involves rounding a final answer to a reasonable number of decimal places or significant figures depending on the context of the problem. This ensures that the answer is both accurate and practical to work with in the given context. |
| C1.10 | Give appropriate upper and lower bounds for data given to a specified accuracy | Upper and lower bounds: Upper and lower bounds are the maximum and minimum possible values for a measurement or calculation. These bounds are used to estimate the true value of a quantity, especially when the actual value is uncertain or cannot be determined with complete accuracy.
Significant figures: Significant figures are the digits that carry meaning in a number. When giving an upper or lower bound, it is important to consider the number of significant figures and to round the answer accordingly. Accuracy and precision: Accuracy refers to how close a measurement or calculation is to the true or accepted value. Precision refers to the degree of exactness or reproducibility of a measurement or calculation. When giving upper and lower bounds, it is important to consider both accuracy and precision in order to give a reasonable estimate of the true value. Error bounds: Error bounds are the limits of the possible error or uncertainty in a measurement or calculation. These bounds are used to ensure that the result of a calculation or measurement is within an acceptable range of accuracy. |
| C1.11 | Demonstrate an understanding of ratio and proportion. Calculate average speed. Use common measures of rate. | Ratio and Proportion: Understand the concept of ratio and proportion, and solve problems using ratios and proportions. Also, solve problems involving direct and inverse proportion.
Average Speed: Understand the concept of speed and average speed, and solve problems involving average speed. Common Measures of Rate: Understand the concept of rate and solve problems involving common measures of rate such as distance per unit time, work per unit time, and cost per unit weight. |
| C1.12 | Calculate a given percentage of a quantity. Express one quantity as a percentage of another. Calculate percentage increase or decrease. | Calculate a given percentage of a quantity: This involves finding a specified percentage of a given quantity, which requires multiplying the percentage value by the quantity.
Express one quantity as a percentage of another: This involves expressing a given quantity as a percentage of another quantity, which requires finding the ratio of the two quantities and multiplying by 100 to convert the ratio to a percentage. Calculate percentage increase or decrease: This involves finding the percentage increase or decrease between two quantities, which requires finding the difference between the two quantities, dividing by the original quantity, and multiplying by 100 to convert the value to a percentage. |
| C1.13 | Use a calculator efficiently. Apply appropriate checks of accuracy | Calculator Functions: Understanding the functions and operations of a calculator including addition, subtraction, multiplication, division, square root, exponentials, logarithms, trigonometric functions, and memory functions.
Efficient Use of Calculator: Using the calculator efficiently by knowing which functions to use for a given problem, inputting the values correctly, and using brackets where necessary to avoid errors. Checking Accuracy: Applying appropriate checks to ensure the accuracy of calculator calculations, such as estimating the answer before calculating, checking that the answer is reasonable, and performing the calculation using a different method to verify the answer. |
| C1.14 | Calculate times in terms of the 24-hour and 12-hour clock. Read clocks, dials and timetables. | Times in terms of 24-hour and 12-hour clock: Students learn to convert times between the 24-hour and 12-hour clock, and to understand the conventions used when writing times in each system.
Reading clocks and dials: Students learn to read and interpret clocks and dials, including analog and digital clocks, as well as other types of gauges and instruments that display numerical data. Timetables: Students learn to read and interpret timetables, which show schedules for events such as public transportation, sporting events, or performances. This includes understanding the layout and format of timetables, as well as calculating time intervals and journey durations based on the information provided. |
| C1.15 | Calculate using money and convert from one currency to another. | Currency exchange rates: Understanding currency exchange rates and how they are used to convert one currency to another.
Currency conversion: The process of converting one currency to another using exchange rates and performing calculations with different currencies. Buying and selling currencies: Understanding how to buy and sell currencies, including commission and transaction fees. Profit and loss in currency exchange: Understanding how to calculate profit and loss when exchanging currencies, including exchange rate fluctuations. Real-world applications: Applying currency conversion and exchange rate calculations to real-world situations, such as international travel, online shopping, and global business transactions. |
| C1.16 | Use given data to solve problems on personal and household finance involving earnings, simple interest and compound interest. Extract data from tables and charts | Personal and Household Finance:
|
| C1.17 | Extended Curriculum Only |
Core 2: Algebra and Graphs
Core 2 focuses on algebraic expressions, equations, and graphing functions.
| Subtopic Number | Subtopic | IGCSE Points to understand |
| C2.1 | Use letters to express generalised numbers and express basic arithmetic processes algebraically. Substitute numbers for words and letters in formulae. Rearrange simple formulae. Construct simple expressions and set up simple equations. | Algebraic expressions: Algebraic expressions are mathematical phrases that use letters, numbers, and symbols to represent quantities and operations. They can be simplified, evaluated, and used in calculations.
Simplifying algebraic expressions: Simplifying algebraic expressions involves combining like terms, removing parentheses, and applying the distributive property. This allows for easier calculations and a clearer representation of the expression. Substituting values: Substituting values involves replacing letters or variables in an algebraic expression with specific numbers. This allows for the evaluation of the expression and the calculation of a specific result. Expanding brackets: Expanding brackets involves applying the distributive property to an expression with brackets. This involves multiplying each term inside the brackets by the term outside the brackets. Factorising: Factorising involves breaking down an expression into its factors. This can help to simplify the expression or identify common factors. Solving equations: Solving equations involves finding the value of the variable that makes the equation true. This can be done by using inverse operations to isolate the variable. Forming equations: Forming equations involves translating a real-world problem into an algebraic equation. This requires an understanding of the problem and the ability to identify the relevant variables and operations. Simultaneous equations: Simultaneous equations are equations that contain two or more variables. They can be solved by either substitution or elimination. Quadratic equations: Quadratic equations are equations that contain a variable raised to the power of two. They can be solved by either factorisation or the quadratic formula. Inequalities: Inequalities are expressions that compare two quantities using inequality symbols such as <, >, ≤, or ≥. They can be solved using similar methods to equations, but the solution is a range of values rather than a single value. |
| C2.2 | Manipulate directed numbers. Use brackets and extract common factors.
Expand products of algebraic expressions. |
Manipulate directed numbers:
Use brackets:
Extract common factors:
|
| C2.3 | Extended Curriculum Only | |
| C2.4 | Use and interpret positive, negative and zero indices. Use the rules of indices. | Use and interpret positive, negative and zero indices: This subtopic covers the use of indices (also known as exponents) in mathematics, including positive, negative, and zero indices. Students will learn how to interpret and use these indices in a variety of contexts, such as scientific notation and algebraic expressions.
Use the rules of indices: This subtopic covers the rules of indices, including how to multiply and divide powers with the same base, raise a power to a power, and use the zero and negative index rules. Students will also learn how to simplify expressions with indices using these rules. |
| C2.5 | Derive and solve simple linear equations in one unknown. Derive and solve simultaneous linear equations in two unknowns. | Derive and solve simple linear equations in one unknown: This subtopic covers the process of deriving and solving linear equations that involve a single unknown variable. Students learn how to simplify equations, isolate the variable, and solve for the unknown value using basic algebraic techniques.
Derive and solve simultaneous linear equations in two unknowns: This subtopic covers the process of deriving and solving simultaneous linear equations that involve two unknown variables. Students learn how to use substitution and elimination methods to solve for the values of both unknowns. They also learn how to interpret and check the solutions to ensure they are valid. |
| C2.6 | Extended Curriculum Only | |
| C2.7 | Continue a given number sequence. Recognise patterns in sequences including the term to term rule and relationships between different sequences. Find and use the nth term of sequences. | Continue a given number sequence: This involves identifying the pattern in a given sequence of numbers and using it to extend the sequence.
Recognise patterns in sequences including the term to term rule and relationships between different sequences: This involves identifying the underlying pattern in a given sequence of numbers and determining the rule for generating subsequent terms. Find and use the nth term of sequences: This involves using the term-to-term rule to determine a formula for the nth term of a sequence, and then using this formula to find specific terms in the sequence. |
| C2.8 | Extended Curriculum Only | |
| C2.9 | Extended Curriculum Only | |
| C2.10 | Interpret and use graphs in practical situations including travel graphs and conversion graphs. Draw graphs from given data. | Interpret and use graphs in practical situations: This subtopic involves interpreting and using different types of graphs, such as line graphs, bar graphs, and pie charts, to understand and present data. Students will learn how to read and interpret graphs and use them to draw conclusions and make predictions.
Travel graphs: A travel graph is a type of graph that shows the distance travelled against time. Students will learn how to read and interpret travel graphs, as well as how to use them to calculate average speed and distance. Conversion graphs: A conversion graph is a type of graph that shows the relationship between two different units of measurement. Students will learn how to use conversion graphs to convert between different units, such as miles and kilometers, or pounds and kilograms. Drawing graphs from given data: In this subtopic, students will learn how to draw graphs from given data, including line graphs, bar graphs, and scatter plots. They will also learn how to choose an appropriate scale for their graphs and how to label the axes and title of the graph. |
| C2.11 | Construct tables of values for functions of the form ax + b, ±x 2 + ax + b, x a (x ≠ 0), where a and b are integer constants. Draw and interpret these graphs. Solve linear and quadratic equations approximately, including finding and interpreting roots by graphical methods. Recognise, sketch and interpret graphs of functions. | Constructing tables of values and drawing graphs for functions:
Solving equations approximately:
Recognizing, sketching, and interpreting graphs of functions:
|
| C2.12 | Extended Curriculum Only | |
| C2.13 | Extended Curriculum Only |
Core 3: Coordinate Geometry
This unit covers coordinate geometry, including plotting points, calculating distances, and understanding gradients.
| Subtopic Number | Subtopic | IGCSE Points to understand |
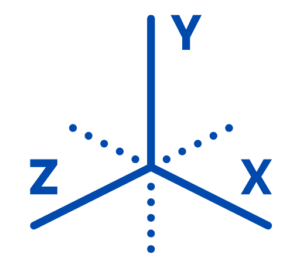
| C3.1 | Demonstrate familiarity with Cartesian coordinates in two dimensions | Understanding Cartesian Coordinates: Cartesian coordinates are a system used to locate points in a plane using two perpendicular lines (axes), the x-axis and y-axis. The point of intersection between these two axes is called the origin. Each point on the plane can be represented by an ordered pair (x,y), where x is the distance from the origin along the x-axis, and y is the distance from the origin along the y-axis.
Plotting Points on the Coordinate Plane: To plot a point on the coordinate plane, we start at the origin and move horizontally (left or right) by the value of the x-coordinate, and then vertically (up or down) by the value of the y-coordinate. The point where these two movements intersect is the point on the plane. Recognizing Quadrants: The plane is divided into four quadrants, numbered counterclockwise from quadrant I (upper right) to quadrant IV (lower right). Each quadrant has a unique combination of positive and negative x and y values. Finding the Distance between Two Points: To find the distance between two points on the plane, we use the distance formula: distance = √((x₂ – x₁)² + (y₂ – y₁)²) where (x₁,y₁) and (x₂,y₂) are the coordinates of the two points. Recognizing Lines and Slopes: A line is a set of points that extends infinitely in both directions. The slope of a line is a measure of how steep it is, and is defined as the change in y over the change in x between any two points on the line. The slope-intercept form of a line is y = mx + b, where m is the slope and b is the y-intercept (where the line crosses the y-axis). Graphing Linear Equations: To graph a linear equation in two variables, we can find two or more points that satisfy the equation, plot them on the plane, and then draw a straight line through them. We can also use the slope-intercept form of the equation to identify the y-intercept and slope, and then graph the line using these values. Understanding Systems of Equations: A system of equations is a set of two or more equations with two or more variables. The solution to a system of equations is the set of values for the variables that make all of the equations true simultaneously. A system of equations can have one, none, or infinitely many solutions. We can solve a system of equations using substitution or elimination, and we can graph the system on the coordinate plane to visualize the solutions. |
| C3.2 | Find the gradient of a straight line | Gradient: The gradient of a straight line is a measure of its steepness. It is calculated by dividing the change in the y-coordinate by the change in the x-coordinate between two points on the line.
Method to find gradient: The gradient of a straight line can be found using the formula: gradient = (change in y-coordinate) / (change in x-coordinate) or simply by using the slope formula, which is (y2 – y1) / (x2 – x1). Interpretation of gradient: The gradient can be interpreted as the rate of change of the dependent variable with respect to the independent variable. A positive gradient indicates an increasing relationship between the variables, while a negative gradient indicates a decreasing relationship. Uses of gradient: The gradient is used in many applications of mathematics, such as finding the equation of a line, determining the rate of change in a physical system, and in calculus to calculate derivatives. |
| C3.3 | Extended Curriculum Only | |
| C3.4 | Interpret and obtain the equation of a straight line graph in the form y = mx + c. | Equation of a Straight Line: The equation of a straight line is an algebraic representation of a line on a coordinate plane. It is written in the form y = mx + c, where m is the gradient of the line and c is the y-intercept of the line.
Finding the Equation of a Straight Line: Given two points on a line, we can find the equation of the line by calculating the gradient of the line and using one of the points to find the y-intercept. Alternatively, if we know the gradient of the line and the y-intercept, we can directly write the equation in the form y = mx + c. Interpreting the Equation of a Straight Line: The equation of a straight line can provide information about the slope of the line, its intercept with the y-axis, and the direction of the line (whether it is rising or falling). Graphing a Straight Line: Given an equation in the form y = mx + c, we can graph the line by plotting the y-intercept (c) and then using the gradient (m) to find additional points on the line. Alternatively, we can use two points on the line to graph it. Applications of Straight Line Graphs: Straight line graphs can be used to model a variety of real-world phenomena, such as distance-time graphs for motion, cost-revenue graphs for business, and temperature-time graphs for weather. By interpreting the slope and intercept of the line, we can make predictions and draw conclusions about the situation being modeled. |
| C3.5 | Determine the equation of a straight line parallel to a given line. | Parallel Lines: Lines are parallel if they have the same gradient (slope) and different y-intercepts. Two parallel lines will never meet or intersect.
Finding the Equation of a Line: To find the equation of a line, you need to know its gradient and y-intercept. This is usually done in the form y = mx + c, where m is the gradient and c is the y-intercept. Point-Slope Form: Another way to find the equation of a line is by using the point-slope form, which uses a point on the line and the gradient to find the equation. The formula is y – y1 = m(x – x1), where (x1, y1) is the given point and m is the gradient. Using Parallel Lines to Find Equations: If you have the equation of one line and need to find the equation of a parallel line, you can use the fact that parallel lines have the same gradient. Simply substitute the gradient of the first line into the equation y = mx + c and solve for the y-intercept. Applications: The concept of parallel lines and finding equations of parallel lines is useful in a variety of real-life situations, such as designing roads, constructing buildings, and creating mathematical models. |
| C3.6 | Extended Curriculum Only |
Core 4: Geometry
Geometry concepts, such as angles, shapes, and transformations, are explored in this unit,also aligning with the comprehensive IGCSE Syllabus for Grade 9 Maths.
| Subtopic Number | Subtopic | IGCSE Points to understand |
| C4.1 | Use and interpret the geometrical terms: point, line, parallel, bearing, right angle, acute, obtuse and reflex angles, perpendicular, similarity and congruence. Use and interpret vocabulary of triangles, quadrilaterals, circles, polygons and simple solid figures including nets. | Point: A point is a location in space that has no dimension or size. It is represented by a dot and is named using a capital letter.
Line: A line is a straight path that extends infinitely in both directions. It has no thickness and is represented by a straight line with two arrowheads. Parallel: Two lines are parallel if they are always the same distance apart and never meet. Bearing: A bearing is a measurement of an angle in degrees, measured clockwise from north. Right angle: A right angle is an angle that measures exactly 90 degrees. Acute angle: An acute angle is an angle that measures less than 90 degrees. Obtuse angle: An obtuse angle is an angle that measures between 90 and 180 degrees. Reflex angle: A reflex angle is an angle that measures between 180 and 360 degrees. Perpendicular: Two lines are perpendicular if they meet at a right angle. Similarity: Two figures are similar if they have the same shape but not necessarily the same size. Congruence: Two figures are congruent if they have the same shape and size. Triangle: A triangle is a closed two-dimensional shape with three straight sides and three angles. Quadrilateral: A quadrilateral is a closed two-dimensional shape with four straight sides and four angles. Circle: A circle is a closed curved shape where all points on the curve are the same distance from the center point. Polygon: A polygon is a closed two-dimensional shape with straight sides. Solid figure: A solid figure is a three-dimensional shape with length, width, and height. Nets: Nets are two-dimensional shapes that can be folded to create three-dimensional figures. |
| C4.2 | Measure and draw lines and angles. Construct a triangle given the three sides using a ruler and a pair of compasses only. | Measure and draw lines: This subtopic covers how to measure the length of a line segment accurately using a ruler, and how to draw straight lines with a ruler.Measure and draw angles: This subtopic covers how to measure angles using a protractor and how to draw angles with a protractor and ruler.
Construct a triangle given the three sides: This subtopic covers how to use a ruler and pair of compasses to construct a triangle given the lengths of its three sides. The process involves drawing three circles with centers at the endpoints of the sides, and then finding the intersection of these circles to locate the vertices of the triangle. |
| C4.3 | Read and make scale drawings. | Scale: A scale is a ratio or proportion that represents the relationship between a measurement on a drawing or map and the actual measurement of the object or area it represents.
Scale drawings: Scale drawings are drawings that show an object, building or area with accurate proportions relative to the actual size of the object. Scale drawings are often used in architecture, engineering, and design. Representing objects on a smaller scale: When representing objects on a smaller scale, the dimensions of the object are reduced by the same factor, which is the scale factor. Representing objects on a larger scale: When representing objects on a larger scale, the dimensions of the object are increased by the same factor, which is the scale factor. Using scales on maps: Maps often use scales to represent the distances between locations accurately. The scale on a map may be represented as a ratio or as a graphical scale bar. Using scales in technical drawings: Technical drawings such as blueprints or engineering plans use scales to accurately represent the dimensions of the object being designed or constructed. Reading and interpreting scale drawings: To read a scale drawing, you need to understand the scale factor and the units of measurement used. You can then use the scale to calculate measurements and dimensions of the object being represented. Making scale drawings: To make a scale drawing, you need to choose an appropriate scale factor and accurately measure the dimensions of the object you are representing. You can then use the scale factor to reduce or enlarge the dimensions of the object and draw the scale drawing with accurate proportions. |
| C4.4 | Calculate lengths of similar figures | Similar figures are figures that have the same shape but may differ in size. In this subtopic, you will learn how to calculate the lengths of corresponding sides of similar figures using scale factors.
|
| C4.5 | Recognise congruent shapes. | Congruent shapes are geometric figures that have the same size and shape. Two shapes are said to be congruent if they can be transformed into each other through rigid motions, such as rotations, reflections, and translations.
Identifying congruent shapes: This involves recognising the characteristics of congruent shapes, such as equal side lengths, equal angles, and identical shapes. It may also involve identifying congruent parts of a shape, such as sides or angles. Using congruence to solve problems: This involves using the concept of congruence to solve various types of problems, such as finding missing side lengths or angles in congruent triangles. It may also involve using congruence to prove the properties of shapes or to solve more complex problems involving multiple shapes. Applying congruence in real-world situations: This involves applying the concept of congruence to real-world situations, such as in architecture or engineering, where precise measurements and identical shapes are important for construction and design. |
| C4.6 | Recognise rotational and line symmetry (including order of rotational symmetry) in two dimensions. | Symmetry: A shape or an object is said to have symmetry if it can be divided into identical parts by a line or a point.
Line Symmetry: A shape has line symmetry if it can be divided into two identical parts by a line, also known as a line of symmetry. Rotational Symmetry: A shape has rotational symmetry if it can be rotated by a certain angle and still look the same. The order of rotational symmetry is the number of times a shape can be rotated to coincide with its original position. Examples: A circle has infinite rotational symmetry, a square has 4 lines of symmetry and rotational symmetry of order 4, a rectangle has 2 lines of symmetry but no rotational symmetry, and a regular hexagon has 6 lines of symmetry and rotational symmetry of order 6. |
| C4.7 | Calculate unknown angles using the following geometrical properties:
• angles at a point • angles at a point on a straight line and intersecting straight lines • angles formed within parallel lines • angle properties of triangles and quadrilaterals • angle properties of regular polygons • angle in a semicircle • angle between tangent and radius of a circle. |
Angles at a point: Angles at a point add up to 360 degrees. Therefore, if you know the value of some of the angles at a point, you can find the value of the missing angle by subtracting the sum of the known angles from 360.
Angles at a point on a straight line and intersecting straight lines: If two straight lines intersect, the opposite angles are equal. Also, if a straight line intersects two parallel lines, the corresponding angles are equal, the alternate angles are equal, and the interior angles on the same side of the transversal add up to 180 degrees. Angles formed within parallel lines: When a transversal intersects two parallel lines, the corresponding angles, alternate angles, and interior angles on the same side of the transversal are equal. Angle properties of triangles and quadrilaterals: A triangle has three interior angles that add up to 180 degrees. In a quadrilateral, the sum of the interior angles is equal to 360 degrees. Special types of quadrilaterals, such as squares, rectangles, and parallelograms, have additional angle properties that can be used to calculate unknown angles. Angle properties of regular polygons: Regular polygons have equal interior angles, which can be calculated by dividing 360 degrees by the number of sides in the polygon. Angle in a semicircle: The angle at the center of a circle formed by two radii is 90 degrees. Therefore, the angle in a semicircle is also 90 degrees. Angle between tangent and radius of a circle: The angle between a tangent and a radius of a circle is 90 degrees. |
Core 5: Mensuration
Core 5 involves the study of mensuration, encompassing the measurement of area, volume, and surface area
| Subtopic Number | Subtopic | IGCSE Points to understand |
| C5.1 | Use current units of mass, length, area, volume and capacity in practical situations and express quantities in terms of larger or smaller units. | Units of mass: Understanding units of mass such as grams, kilograms, and tonnes, and converting between them in practical situations.
Units of length: Understanding units of length such as millimeters, centimeters, meters, and kilometers, and converting between them in practical situations. Units of area: Understanding units of area such as square centimeters, square meters, and hectares, and converting between them in practical situations. Units of volume: Understanding units of volume such as cubic centimeters, cubic meters, and liters, and converting between them in practical situations. Units of capacity: Understanding units of capacity such as milliliters and liters, and converting between them in practical situations. Expressing quantities in terms of larger or smaller units: Using prefixes such as kilo-, mega-, milli-, and micro- to express quantities in larger or smaller units, and converting between them in practical situations. Practical applications: Applying knowledge of units of measurement and conversions to practical situations, such as measuring ingredients for cooking, calculating distances for travel, and estimating volumes of containers. |
| C5.2 | Carry out calculations involving the perimeter and area of a rectangle, triangle, parallelogram and trapezium and compound shapes derived from these. | Perimeter of a rectangle: The perimeter of a rectangle is the total distance around its sides. It is calculated by adding the lengths of all the sides.
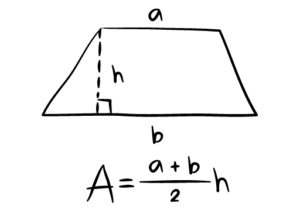
Area of a rectangle: The area of a rectangle is the amount of space inside the shape. It is calculated by multiplying the length by the width. Perimeter of a triangle: The perimeter of a triangle is the total distance around its sides. It is calculated by adding the lengths of all the sides. Area of a triangle: The area of a triangle is the amount of space inside the shape. It is calculated by multiplying half the base by the height. Perimeter of a parallelogram: The perimeter of a parallelogram is the total distance around its sides. It is calculated by adding the lengths of all the sides. Area of a parallelogram: The area of a parallelogram is the amount of space inside the shape. It is calculated by multiplying the base by the height. Perimeter of a trapezium: The perimeter of a trapezium is the total distance around its sides. It is calculated by adding the lengths of all the sides. Area of a trapezium: The area of a trapezium is the amount of space inside the shape. It is calculated by multiplying the average of the two parallel sides by the height. Compound shapes derived from rectangles, triangles, parallelograms, and trapeziums: Compound shapes are made up of two or more simple shapes. The perimeter and area of compound shapes can be calculated by adding or subtracting the perimeters and areas of the individual shapes. |
| C5.3 | Carry out calculations involving the circumference and area of a circle. Solve simple problems involving the arc length and sector area as fractions of the circumference and area of a circle. | Circumference of a circle: The circumference of a circle is the distance around the edge of the circle.
Area of a circle: The area of a circle is the amount of space inside the circle. Arc length of a circle: The arc length of a circle is the length of a portion of the circumference of a circle. Sector of a circle: A sector of a circle is a region bounded by two radii and an arc, with a central angle measured in radians. Sector area of a circle: The sector area of a circle is the area of a sector of a circle, which is a fraction of the total area of the circle. |
| C5.4 | Carry out calculations involving the surface area and volume of a cuboid, prism and cylinder. Carry out calculations involving the surface area and volume of a sphere, pyramid and cone. | Surface Area and Volume of a Cuboid: Learn how to calculate the surface area and volume of a cuboid, which is a 3D figure with six rectangular faces.
Surface Area and Volume of a Prism: Learn how to calculate the surface area and volume of a prism, which is a 3D figure with two identical and parallel faces that are polygonal in shape. Surface Area and Volume of a Cylinder: Learn how to calculate the surface area and volume of a cylinder, which is a 3D figure with a circular base and a curved surface that is perpendicular to the base. Surface Area and Volume of a Sphere: Learn how to calculate the surface area and volume of a sphere, which is a 3D figure with all points on its surface equidistant from its center. Surface Area and Volume of a Pyramid: Learn how to calculate the surface area and volume of a pyramid, which is a 3D figure with a polygonal base and triangular faces that meet at a common vertex. Surface Area and Volume of a Cone: Learn how to calculate the surface area and volume of a cone, which is a 3D figure with a circular base and a curved surface that tapers to a point (apex) at the top. |
| C5.5 | Carry out calculations involving the areas and volumes of compound shapes. | Compound shapes: Compound shapes are shapes that are made up of two or more simpler shapes. Examples include shapes made up of rectangles, triangles, and semicircles.
Decomposing compound shapes: Decomposing compound shapes involves breaking them down into simpler shapes so that their area or volume can be calculated more easily. Area of compound shapes: To find the area of a compound shape, you can decompose it into simpler shapes, calculate the area of each shape, and then add them together. Volume of compound shapes: To find the volume of a compound shape, you can decompose it into simpler shapes, calculate the volume of each shape, and then add them together. |
Core 6: Trigonometry
Trigonometric functions and their applications, in accordance with the comprehensive IGCSE Maths Syllabus, are the focus of this unit.
| Subtopic Number | Subtopic | IGCSE Points to understand |
| 6.1 | Interpret and use three-figure bearings. | Bearings are used to describe directions and angles in navigation and surveying.
A bearing is an angle measured clockwise from north, written as a three-digit number, such as 030°. The first two digits represent the angle measured in degrees, and the third digit represents the angle measured in minutes. Bearings can be used to describe the direction from one point to another, such as the direction of a ship from a lighthouse. Bearings can be used to calculate the distance between two points using trigonometry. |
| 6.2 | Apply Pythagoras’ theorem and the sine, cosine and tangent ratios for acute angles to the calculation of a side or of an angle of a right angled triangle. | Pythagoras’ Theorem: This theorem states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. This can be used to find the length of any side of a right-angled triangle if the lengths of the other two sides are known.
Sine, Cosine, and Tangent Ratios: These are trigonometric ratios that relate the angles and sides of a right-angled triangle. Sine is the ratio of the length of the side opposite the angle to the length of the hypotenuse, cosine is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse, and tangent is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. These ratios can be used to find the length of a side or the measure of an angle in a right-angled triangle if one length and one angle are known. Calculation of a Side or Angle: These concepts can be used to find the length of a side or the measure of an angle in a right-angled triangle when some information is given. The process involves identifying the right angle, labeling the sides with their opposite angles and trigonometric ratios, and applying the relevant formula to find the unknown quantity. |
| 6.3 | Extended Curriculum Only | |
| 6.4 | Extended Curriculum Only | |
| 6.5 | Extended Curriculum Only |
Core 7: Vectors and Transformations
This unit introduces vectors and transformations, including vector operations and geometric transformations.
| Subtopic Number | Subtopic | IGCSE Points to understand |
| 7.1 | Describe a translation by using a vector represented by e.g. x y e o, AB or a. Add and subtract vectors. Multiply a vector by a scalar | Translation: A transformation that moves every point of a shape by a fixed distance in a fixed direction.
Vector: A quantity that has both magnitude and direction. Vectors are commonly represented by arrows, and the length of the arrow corresponds to the magnitude of the vector while the direction of the arrow indicates its direction. Vector notation: The notation used to represent vectors, typically written in the form <x, y>, where x and y are the horizontal and vertical components of the vector, respectively. Adding vectors: The process of combining two or more vectors to form a single vector. Subtracting vectors: The process of finding the difference between two vectors by adding the opposite of the second vector to the first vector. Scalar multiplication: The process of multiplying a vector by a scalar (a real number). This results in a new vector with the same direction as the original vector but a different magnitude. |
| 7.2 | Reflect simple plane figures in horizontal or vertical lines. Rotate simple plane figures about the origin, vertices or midpoints of edges of the figures, through multiples of 90°. Construct given translations and enlargements of simple plane figures. Recognise and describe reflections, rotations, translations and enlargements. | Reflect simple plane figures in horizontal or vertical lines: This involves reflecting a figure over a horizontal or vertical line to create a new figure that is a mirror image of the original.
Rotate simple plane figures about the origin, vertices, or midpoints of edges of the figures through multiples of 90°: This involves rotating a figure about a specific point on the coordinate plane (e.g. the origin, a vertex, or a midpoint of an edge) through 90, 180, or 270 degrees. Construct given translations and enlargements of simple plane figures: This involves translating or enlarging a figure based on given instructions. Recognize and describe reflections, rotations, translations, and enlargements: This involves identifying and describing the type of transformation that has been applied to a figure, such as a reflection, rotation, translation, or enlargement. |
| 7.3 | Extended Curriculum Only |
Core 8: Probability
Probability theory, including events, probability calculations, and conditional probability, is covered in this unit, as per the IGCSE Math Syllabus.
| Subtopic Number | Subtopic | IGCSE Points to understand |
| 8.1 | Calculate the probability of a single event as either a fraction, decimal or percentage. | Probability of a single event: Probability is a measure of the likelihood of an event occurring. It is calculated as the number of favourable outcomes divided by the total number of possible outcomes. For a single event, the probability can be expressed as a fraction, decimal or percentage.
Calculating probability: To calculate the probability of a single event, we need to determine the number of favourable outcomes and the total number of possible outcomes. The probability is then calculated by dividing the number of favourable outcomes by the total number of possible outcomes. The result can be expressed as a fraction, decimal or percentage. Events and outcomes: An event is a specific outcome or set of outcomes of an experiment. Outcomes are the possible results of an experiment. For example, when tossing a coin, the possible outcomes are heads and tails. Experimental and theoretical probability: Experimental probability is the probability of an event based on actual observations or experiments. Theoretical probability is the probability of an event calculated using mathematical formulas or models. Sample space: The sample space is the set of all possible outcomes of an experiment. It can be represented using a list, table or diagram. Mutually exclusive events: Mutually exclusive events are events that cannot occur at the same time. For example, when rolling a dice, the events of getting an even number and getting an odd number are mutually exclusive. Independent events: Independent events are events where the occurrence of one event does not affect the probability of the other event occurring. For example, when flipping a coin twice, the outcome of the first flip does not affect the outcome of the second flip. |
| 8.2 | Understand and use the probability scale from 0 to 1. | Probability scale: Understanding and using the probability scale from 0 to 1, where 0 represents an impossible event
and 1 represents a certain event. Probability of an event: Calculating the probability of an event using the probability scale and expressing it as a fraction, decimal, or percentage. Theoretical probability: Understanding and calculating the theoretical probability of an event using the formula: P(event) = Number of favorable outcomes / Total number of possible outcomes. Experimental probability: Understanding and calculating the experimental probability of an event using the formula: P(event) = Number of times event occurred / Total number of trials. Mutually exclusive events: Understanding and identifying mutually exclusive events, where the occurrence of one event excludes the occurrence of another event. Independent events: Understanding and identifying independent events, where the occurrence of one event does not affect the probability of the occurrence of another event. Dependent events: Understanding and identifying dependent events, where the occurrence of one event affects the probability of the occurrence of another event. |
| 8.3 | Understand that the probability of an event occurring = 1 – the probability of the event not occurring. | This subtopic explains the concept of complementary events in probability, where the probability of an event occurring is equal to 1 minus the probability of the event not occurring. It involves understanding the relationship between the probability of an event and its complementary event, and how to use this relationship to find the probability of the event. Examples of complementary events include getting a head or a tail when flipping a coin, or rolling a number that is either odd or even on a dice. |
| 8.4 | Understand relative frequency as an estimate of probability. Expected frequency of occurrences. | Relative frequency as an estimate of probability: Relative frequency is a method used to estimate the probability of an event occurring by calculating the frequency of its occurrence relative to the total number of observations. The more observations made, the more accurate the estimate becomes.
Expected frequency of occurrences: Expected frequency is the anticipated number of times an event is expected to occur over a certain period based on probability calculations. It is calculated by multiplying the total number of observations by the probability of the event occurring. For example, if the probability of a certain event occurring is 0.25 and there are 100 observations, the expected frequency would be 25. |
| 8.5 | Calculate the probability of simple combined events, using possibility diagrams, tree diagrams and Venn diagrams. | Possibility diagrams: Possibility diagrams are diagrams that show all the possible outcomes of a given event. They are useful in calculating the probability of simple combined events.
Tree diagrams: Tree diagrams are diagrams that show the possible outcomes of a sequence of events. They are useful in calculating the probability of complex events. Venn diagrams: Venn diagrams are diagrams that show the relationships between different sets of data. They are useful in calculating the probability of events that involve more than one set of data. Calculating the probability of simple combined events: Simple combined events are events that involve more than one possible outcome. The probability of these events can be calculated using formulas and diagrams. Using possibility diagrams to calculate probability: Possibility diagrams can be used to calculate the probability of simple combined events by counting the number of possible outcomes and dividing by the total number of outcomes. Using tree diagrams to calculate probability: Tree diagrams can be used to calculate the probability of complex events by multiplying the probabilities of each event in the sequence. Using Venn diagrams to calculate probability: Venn diagrams can be used to calculate the probability of events that involve more than one set of data by analyzing the overlaps between the sets. Expected value of occurrences: Expected value is a measure of the average outcome of a given event over a large number of trials. It can be calculated by multiplying the probability of each outcome by its corresponding value and summing the products. |
| 8.6 | Extended Curriculum Only |
Core 9: Statistics
In line with the comprehensive IGCSE Syllabus for Maths, this unit explores statistical concepts, including data collection, analysis, and interpretation, as essential components of mathematical understanding.
| Subtopic Number | Subtopic | IGCSE Points to understand |
| 9.1 | Collect, classify and tabulate statistical data. | Data collection: The process of gathering information, usually through surveys, experiments, or observations, that can be used to analyze and draw conclusions about a population or sample.
Types of data: Data can be classified as qualitative or quantitative. Qualitative data describes qualities or characteristics, while quantitative data measures quantities or amounts. Organizing data: Data can be organized in tables, charts, graphs, or frequency distributions. This helps to identify patterns, trends, and outliers in the data. Measures of central tendency: Mean, median, and mode are statistical measures used to describe the center of a dataset. Measures of dispersion: Range, variance, and standard deviation are statistical measures used to describe the spread of a dataset. Frequency distributions: A frequency distribution is a table that shows how many times each value or range of values occurs in a dataset. Bar charts and histograms: Bar charts and histograms are graphical representations of frequency distributions. Scatter plots: Scatter plots are used to show the relationship between two variables. They are useful for identifying trends or patterns in the data. Stem-and-leaf plots: Stem-and-leaf plots are a method for organizing and displaying numerical data in a way that shows the distribution of the data. |
| 9.2 | Read, interpret and draw simple inferences from tables and statistical diagrams. Compare sets of data using tables, graphs and statistical measures. Appreciate restrictions on drawing conclusions from given data. | Read, interpret and draw simple inferences from tables and statistical diagrams: Students will learn how to read and interpret statistical data presented in tables and diagrams such as bar charts, pie charts, and line graphs. They will also learn how to draw inferences from this data, such as identifying trends and patterns.
Compare sets of data using tables, graphs, and statistical measures: This subtopic focuses on comparing different sets of data using statistical measures such as the mean, median, and mode. Students will also learn how to create and interpret different types of graphs to compare data, such as scatter plots and box-and-whisker plots. Appreciate restrictions on drawing conclusions from given data: This subtopic will help students understand the limitations of statistical data and the need to be cautious when drawing conclusions. They will learn how to identify potential biases and errors in data and how to address them. Students will also learn about the importance of sample size and how it affects the reliability of statistical data. |
| 9.3 | Construct and interpret bar charts, pie charts, pictograms, stem-and-leaf diagrams, simple frequency distributions, histograms with equal intervals and scatter diagrams. | Bar charts: A bar chart is a graph that represents data using rectangular bars. The height of each bar corresponds to the size of the category it represents. Bar charts can be used to compare data across different categories.
Pie charts: A pie chart is a circular graph that shows the distribution of data across different categories. The size of each slice of the pie represents the proportion of the data that falls into that category. Pictograms: A pictogram is a chart that uses pictures or symbols to represent data. The size of the picture or symbol corresponds to the value of the data it represents. Stem-and-leaf diagrams: A stem-and-leaf diagram is a way to display data using digits. The stems represent the tens or hundreds digit, and the leaves represent the ones digit. This allows for easy comparison of data values. Simple frequency distributions: A simple frequency distribution is a table that shows the number of times each data value appears in a dataset. Histograms with equal intervals: A histogram is a graph that displays data using rectangular bars. The bars are arranged side-by-side, with each bar representing a range of data values. The height of each bar corresponds to the frequency of data values within that range. Scatter diagrams: A scatter diagram is a graph that shows the relationship between two variables. The variables are plotted on the x and y axes, and each point on the graph represents a data value for both variables. |
| 9.4 | Calculate the mean, median, mode and range for individual and discrete data and distinguish between the purposes for which they are used. | Mean: The mean is the average of a set of data. To find the mean, add up all the values and divide by the number of values in the data set. The mean is commonly used to summarize a set of data.
Median: The median is the middle value in a set of data when the values are arranged in numerical order. If there are an even number of values, the median is the average of the two middle values. The median is used to describe the middle of a set of data, and is less affected by extreme values than the mean. Mode: The mode is the value that appears most frequently in a set of data. A data set may have more than one mode, or no mode at all. The mode is used to describe the most common value or values in a set of data. Range: The range is the difference between the largest and smallest values in a set of data. The range is used to describe the spread or variability of a set of data. |
| 9.5 | Extended Curriculum Only | |
| 9.6 | Extended Curriculum Only | |
| 9.7 | Understand what is meant by positive, negative and zero correlation with reference to a scatter diagram. | Correlation: Correlation is a statistical measure that indicates how strongly two variables are related to each other.
Positive correlation: When the values of two variables increase or decrease together, it is known as a positive correlation. In a scatter diagram, the points on the graph will be arranged in a rising trend from left to right. Negative correlation: When one variable increases while the other decreases, it is known as negative correlation. In a scatter diagram, the points on the graph will be arranged in a falling trend from left to right. Zero correlation: When there is no apparent relationship between two variables, it is known as zero correlation. In a scatter diagram, the points will be randomly scattered across the graph without any trend or pattern. |
| 9.8 | Draw, interpret and use lines of best fit by eye | Drawing lines of best fit: A line of best fit is a straight line that is drawn through the center of a set of data points on a scatter plot. It is used to show the general trend or pattern in the data. To draw a line of best fit by eye, you should try to make the line as close as possible to all the data points.
Interpreting lines of best fit: Once a line of best fit has been drawn, you can use it to make predictions or estimates about other data points that are not on the scatter plot. The slope of the line of best fit gives an indication of the direction and strength of the relationship between the variables. Using lines of best fit: Lines of best fit can be used to make predictions or estimates about other data points that are not on the scatter plot. For example, if you have data on the ages and heights of a group of people, you could use a line of best fit to predict the height of someone based on their age. |
READ ALSO: Comprehensive IGCSE Physics Syllabus