By the end of this chapter, you should be familiar with:

• Finding distance between two points in 3-D space
• Finding the midpoint of a line segment in 3-D space
• Volume and surface area of solids
• The size of angle between two lines
• Finding sides and angles of a right-angled triangle using trigonometric ratios.
• Sine and cosine rule
• Computing the area of a triangle using the formula
• Solving problems using trigonometry
• Solving problems involving compass bearings

MEASUREMENT IN THREE DIMENSIONS

DISTANCE BETWEEN TWO POINTS IN 3-D

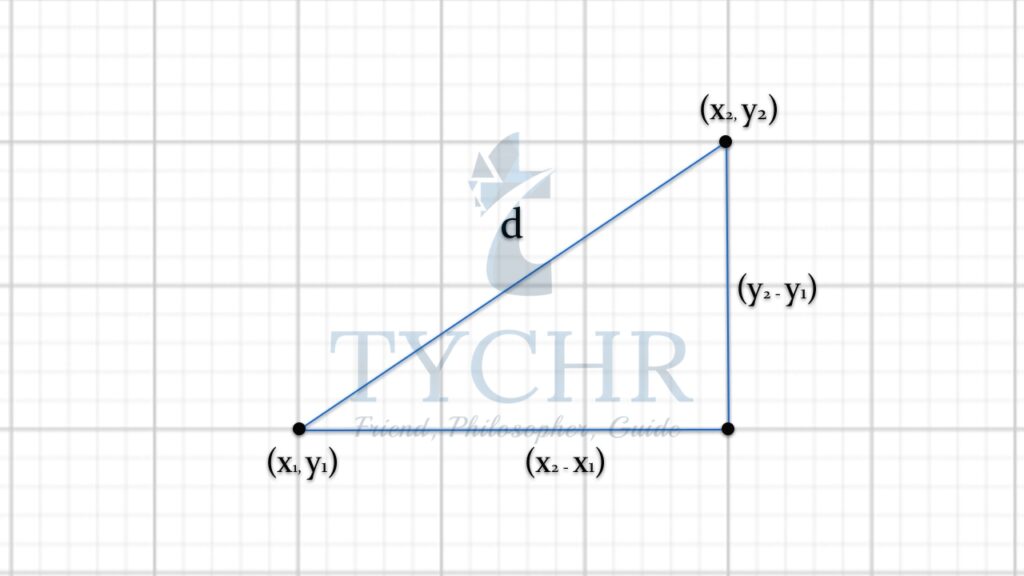
We are familiar with the distance between 2 point in 2-D plane.

The distance d between 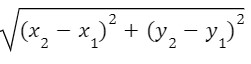2-points (x₁,y₁) and (x₂,y₂) will be- (By pythagorus theorem)

Now, the distance between 2-points in 3-D plane can be calculated easily:
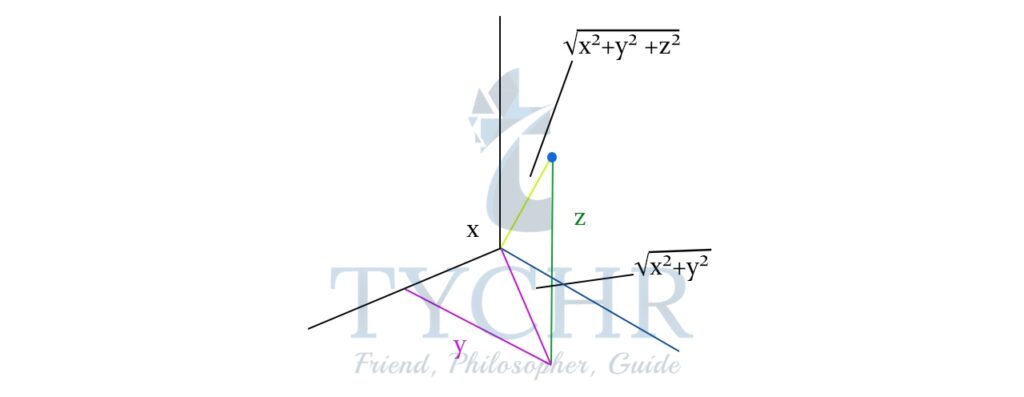
Consider 2 points in the 3-D plane- (x₁, y₁, z₁) and (x₂, y₂, z₂).

Let the distance (x₂-x₁ )=x
(y₂-y₁)=y
(z₂-x₁)=z

From the diagram, and the use of pythagorus theorem, it can be deduced that-

MIDPOINT OF LINE SEGMENT IN 3-D

We are familiar with the midpoint M of a line segment in 2-D plane with endpoints (x₁,y₁) and (x₂,y₂). It has the coordinates- M((x₁+x₂)/2 , (y₁+y₂)/2) i.e. the average of x-coordinates and y-coordinates respectively.

Similarly, The midpoint M of a line segment in 3-D plane with endpoints (x₁,y₁,z₁) and (x₂,y₂,z₂). will be-
M = ((x₁+x₂)/2 , (y₁+y₂)/2 , (z₁+z₂)/2)

Ex. Find the midpoint and length of AB when A is (1,0,-2) and B is (3,2,4)
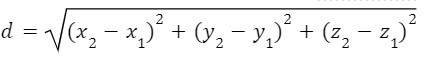
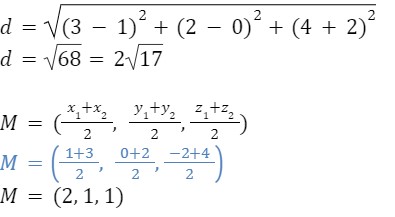
Applying the distance formula – M = ((x₁+x₂)/2 , (y₁+y₂)/2 , (z₁+z₂)/2)
M = ((1+3)/2 , (0+2)/2 , (-2+4)/2)
M = (2, 1, 1 )

VOLUME AND SURFACE AREA OF 3-D SOLIDS

Feature of various solids:

1. Cuboid
   
2. Sphere
   
3. Prism
   
4. Pyramid
   
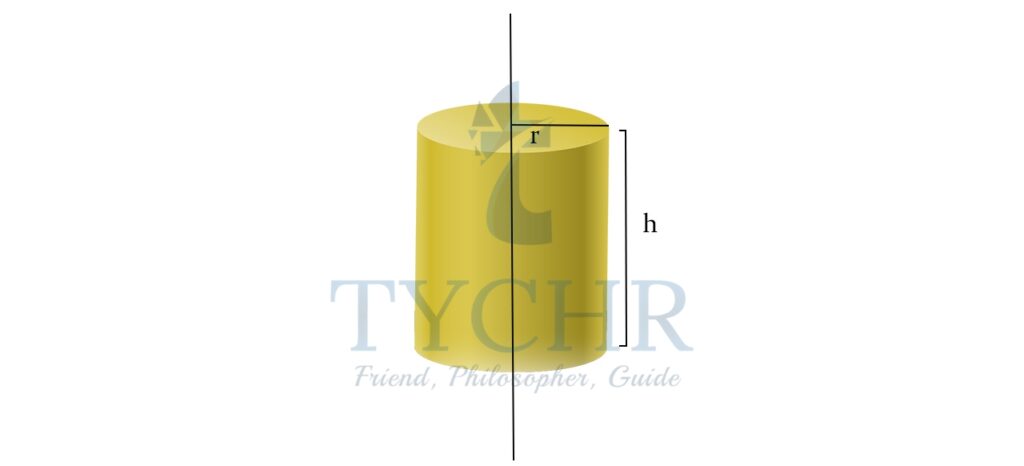
5. Cylinder
   
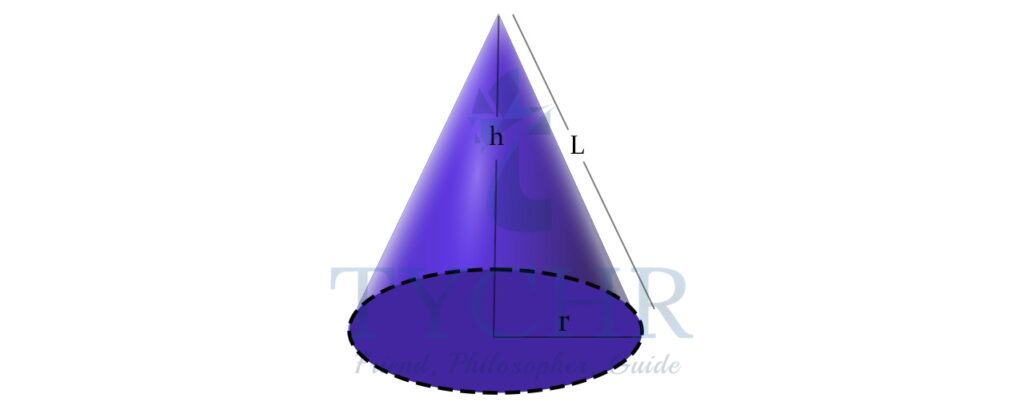
6. Cone
   

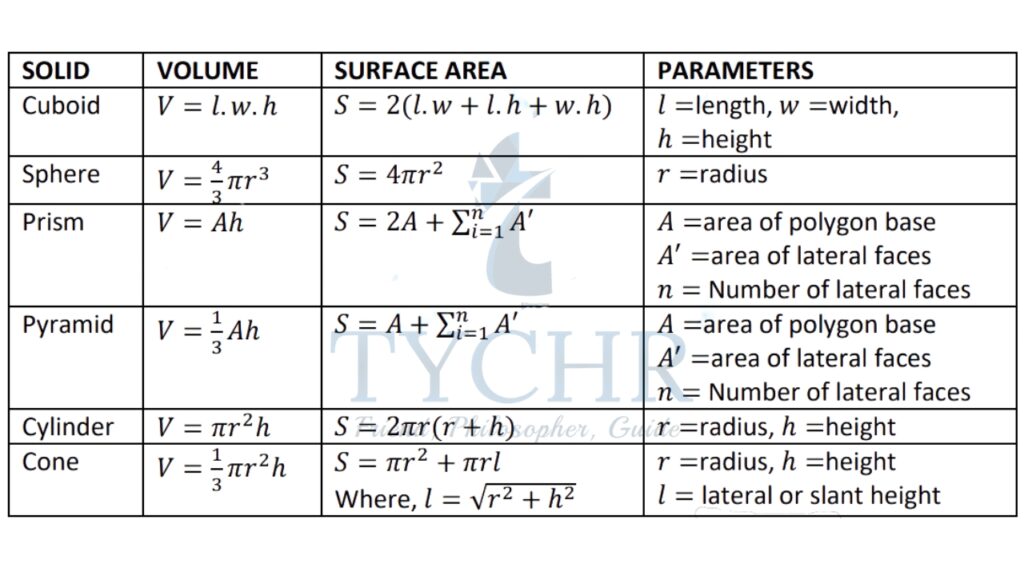
The list of formulas required:

SOLID VOLUME SURFACE AREA PARAMETERS

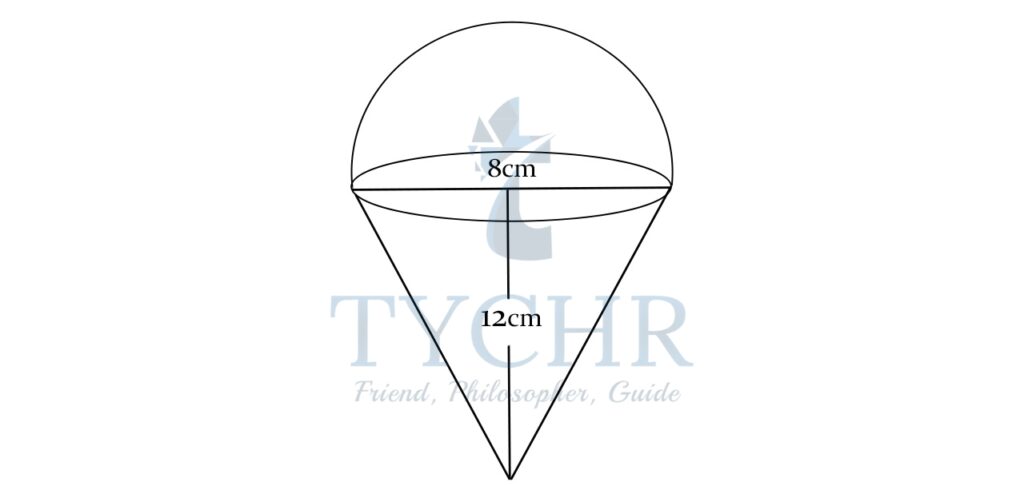
Ex. An ice cream cone is in the shape of a hemisphere sitting on top of a cone. What is the volume and surface area of the ice cream cone? The height of the cone is 12cm and the radius of the hemisphere is 4cm.

r=4cm, h=12cm
Let the slant height be l
𝑙 = √(12²+4²) = 𝑙 = 4√10

Volume of ice-cream cone(VEx. Find the volume and surface area of the following prism: )= Volume of cone + volume of hemisphere
𝑉 = (1/3)𝜋𝑟²ℎ + (2/3)𝜋𝑟³      (Volume of hemisphere is half that of sphere)
𝑉 = ((1/3) × (22/7) × 4² × 12) + ((2/3) × (22/7) × 4³ )
V=201.14+134.09
V=335.23 cm³

Surface area of ice-cream cone(S)= Lateral surface area of cone + surface area of hemisphere
S=πrl+2πr²
𝑆 = ((22/7) × 4 × 4√10) + (2 ×(22/7) × 4² )
S=259.58 cm2

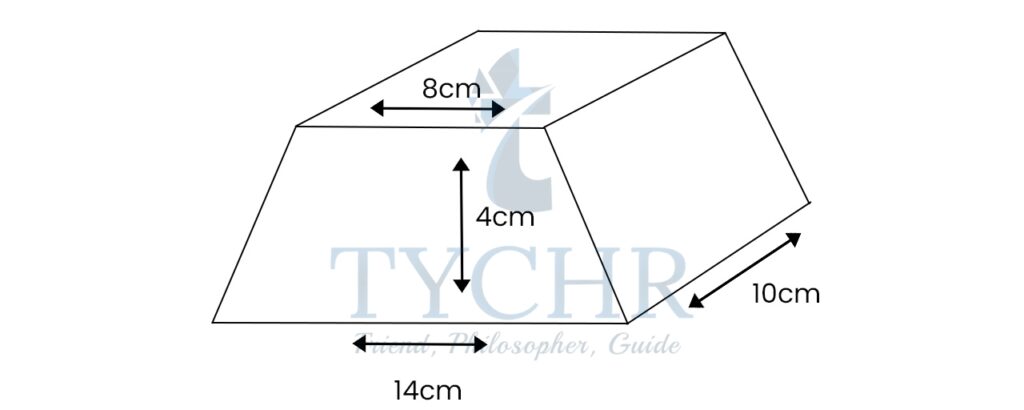
Ex. Find the volume and surface area of the following prism:
Area of base polygon (A) = Area of the trapezium= (1/2) (14 + 8) × 4 = 44 cm²
Volume of prism= Ah=44×10=440 cm3
The slant side of trapezium =√(4²+3² )=5 cm
Area of lateral faces (A’ )= Area of rectangle=10×5=50 cm2
Surface area= 2A+4A’=2(44)+4(50)=288 cm2

RIGHT-ANGLED TRIANGLE TRIGONOMETRY

RIGHT-ANGLED TRIANGLES

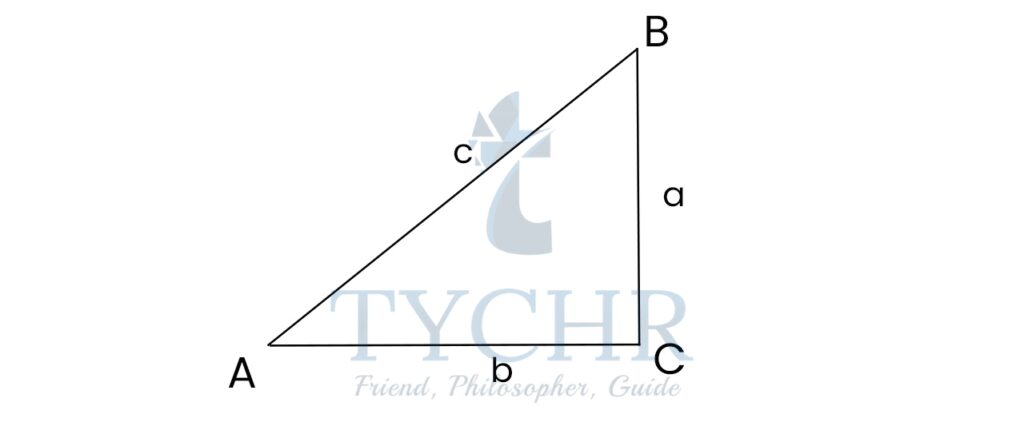
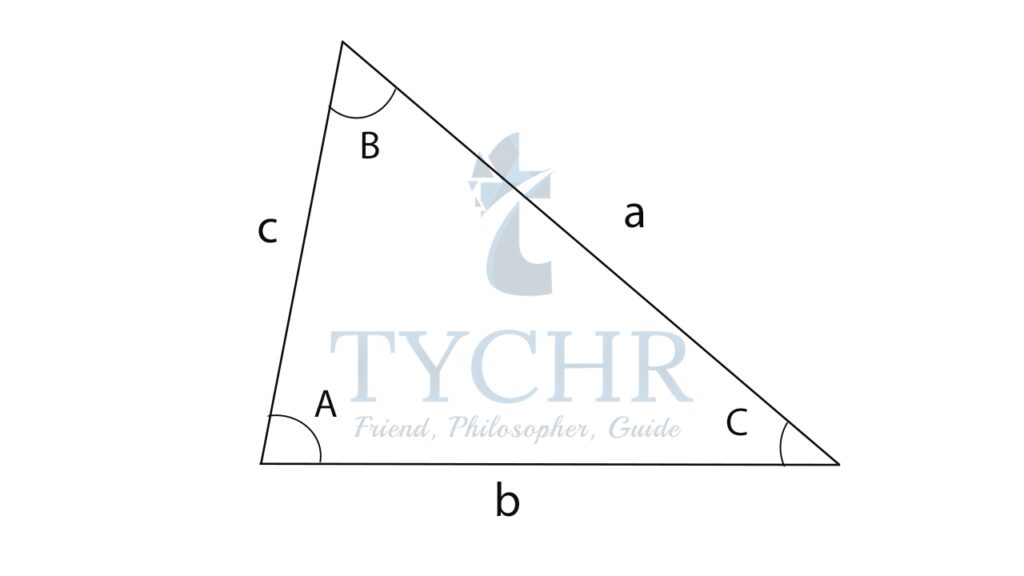
A convenctional notation of a right-angled triangle is shown below:

Here, A, B and C are vertices, and a,b and c are the sides.
For angles, we usually use α,β or θ.

TRIGONOMETRY WITH TRIANGLES

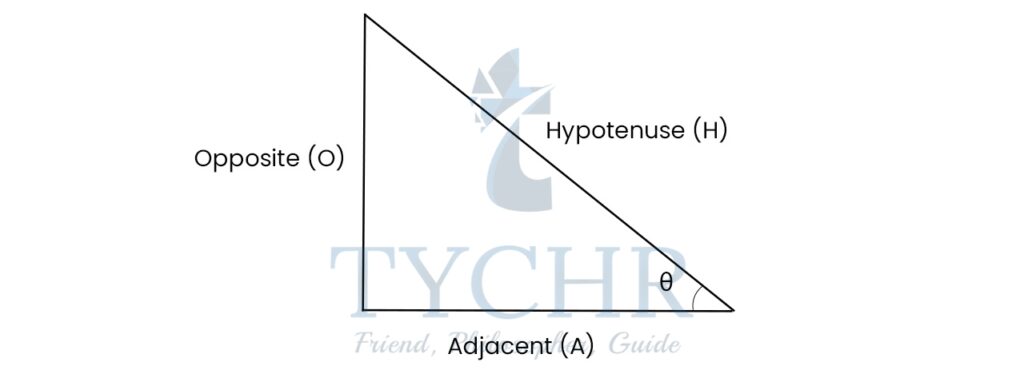
If θ is an acute angle of a right-angled triangle, then:

sin 𝜃 = Side oppositeθ / Hypotenuse
cos 𝜃 = Side adjacentθ/Hypotenuse
tan 𝜃 = Side oppositeθ/Side adjacent θ

Note: Properties of similar triangles are the foundation of right-angled triangle trigonometry. Regardless of the size of the triangle, if the ratio of any two sides remain constant (trigonometric ratio), θ will be same and the triangles will be similar.

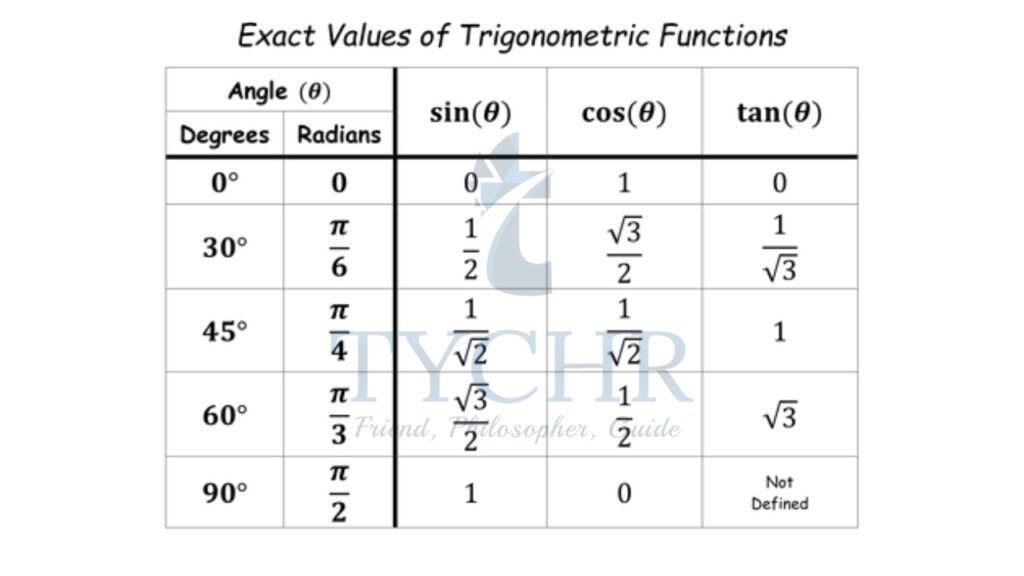
In the previous chapter, we the values of sine, cosine and tangent for common acute angles, let’s review them again. (One must memorise these for certain questions):

FINDING UNKNOWNS OF RIGHT-ANGLED TRIANGLES

We can use Pythagoras’s theorem and trigonometric functions to find the size of any unknown side or angle.
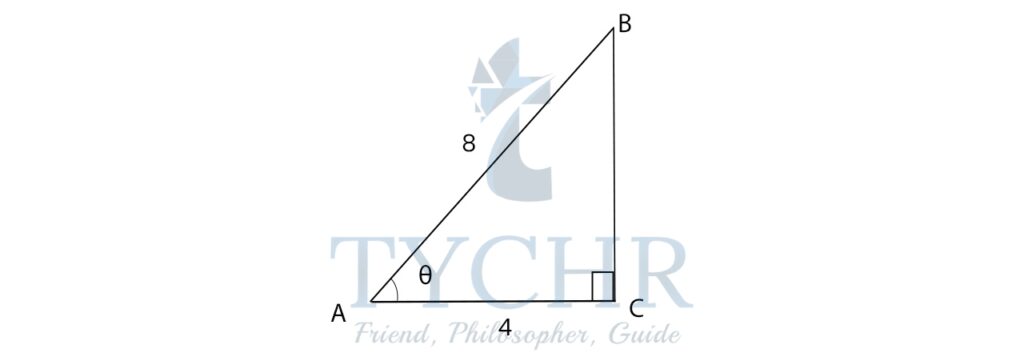
Ex. Find the value of θ:

Adjacent side=4
Hypotenuse=8
We know that
cos 𝜃 = adjacent side/hypotenuse = 4/8 = 1/2
The value of cosine is 1/2 at 𝜃 = 𝜋/3

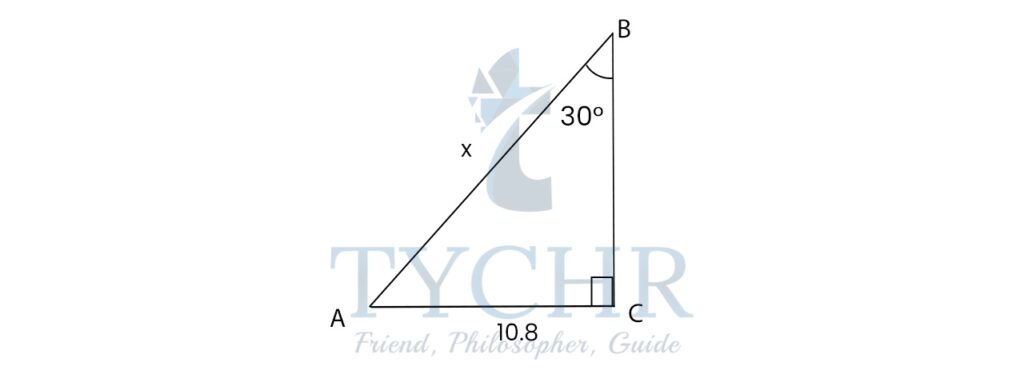
Ex. Find the value of x:

Opposite side=10.8
Hypotenuse=x
θ=30⁰
We know that sin 𝜃 = opposite side/hypotenuse
sin30 = 10.8/𝑥
1/2 = 10.8 /𝑥
𝑥 = 21.6

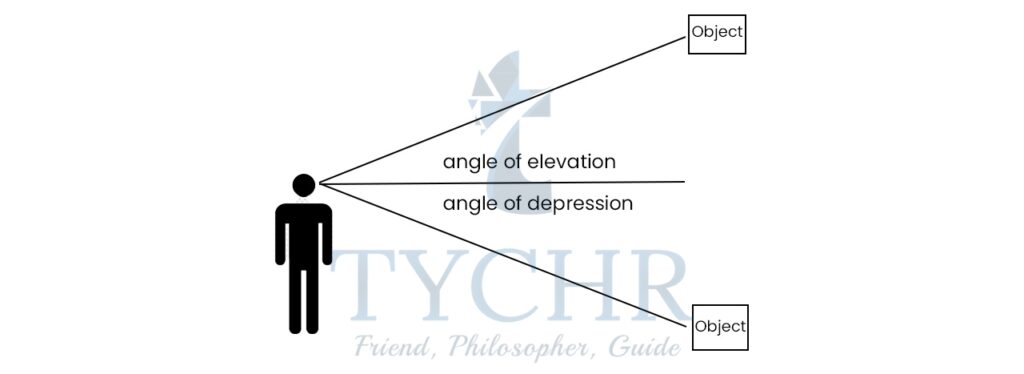
ANGLES OF DEPRESSION AND ELEVATION

Angle of elevation is the angle up from the horizontal and the line from the object to the person’s eye.
Angle of depression is the angle down from the horizontal and the line from the object to the person’s eye.

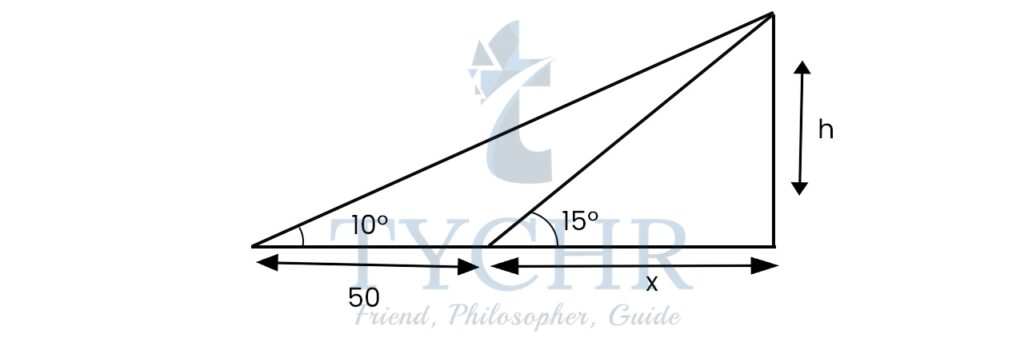
Ex. A man is moving towards a wall with height h. The angle of elevation of a point on the top of the wall increases from 10⁰ to 15⁰ as the man walks a distance of 50 metres. Find h.

From smaller triangle- tan15 = h/x

From larger triangle- tan15 = h/x
Taking the value of h from both of the above equations and setting them equal:
x tan⁡15=(x+50)tan⁡10
x tan⁡15=x tan⁡10+50 tan⁡10
𝑥 = 50tan10/(tan 15−tan10)
x=96.225

Substituting the value of x in h=x tan⁡15
h=96.225 tan⁡15
h=25.783

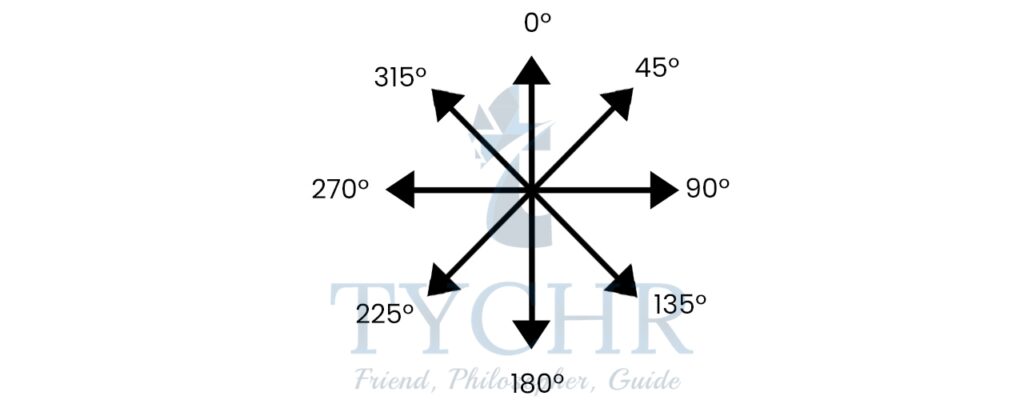
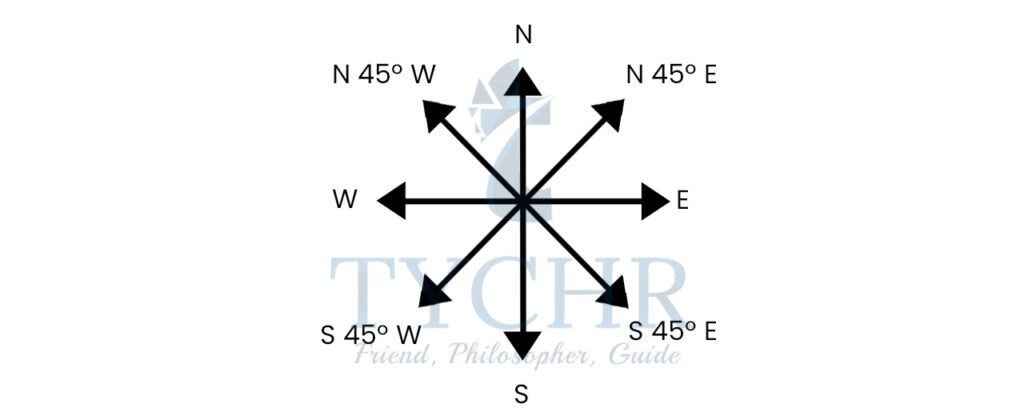
BEARINGS

A bearing is used to indicate the direction of an object from a given point.
Three-figure bearings are measured clockwise from North, and can be written as three figures, such as 145°, 30°, or 335°.

Compass bearings are measured from either North or from South, and can be written such as N20°E, N55°W, S36°E, or S67°W, where the angle between the compass directions is less than 90°.

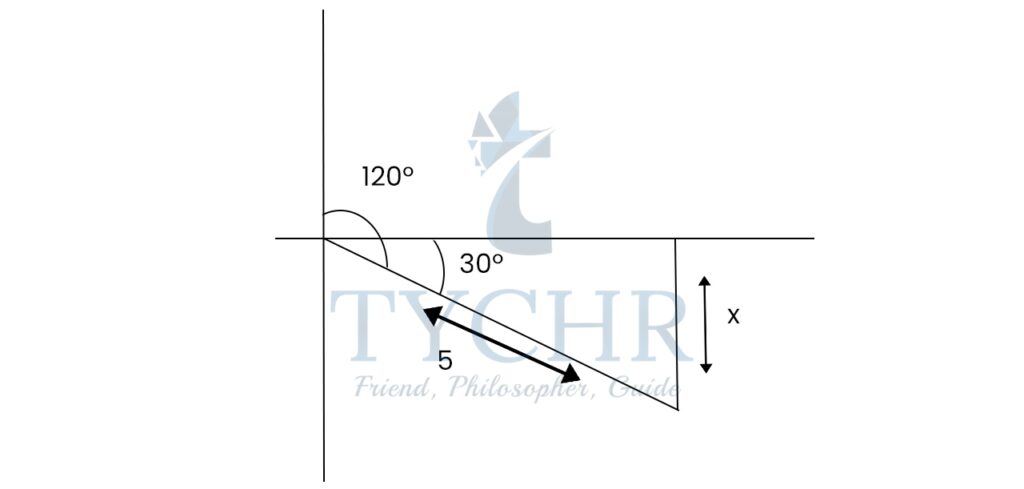
Ex. Andrew runs 5 km on a bearing of 120° from the start. How far south has he travelled?

sin30°=x/5
x = 5sin30°
x = 5/2 = 2.5
Andrew travelled 2.5 km south.

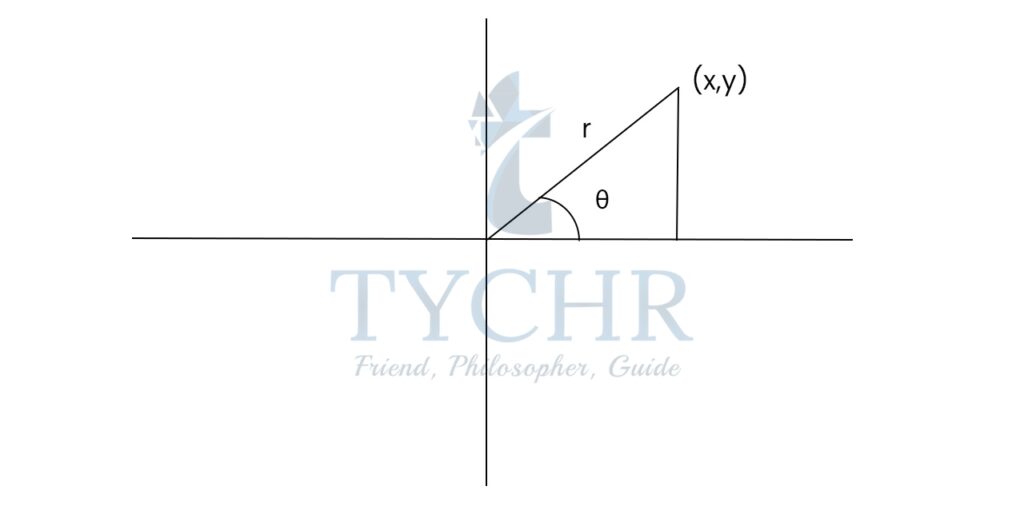
TRIGONOMETRIC FUNCTIONS OF ANY ANGLE

TRIGONOMETRIC RATIOS OF ANGLES WHICH ARE NOT ACUTE

Consider a triangle on the coordinate axes:

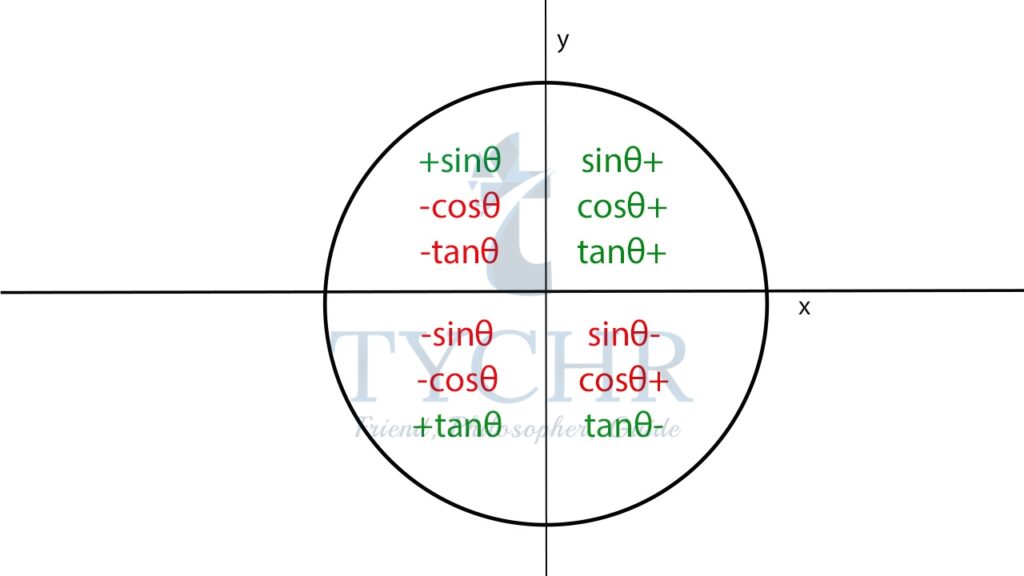
By pythagorus theorem, r²=x²+y²
r = √(x²+y²)
sin𝜃 = y/r, cos𝜃 = x/r, tan𝜃 = y/x

Extending this idea to angles greater than 90°:
Ex. Find the sine, cosine and tangent of the obtuse angle that measures 150°.

The angle is in the 2nd quadrant, where sine is positive and cosine and tangent are negative. The value of the ratios at 150° will be same as that of 30°.
sin150°=1/2,
cos150° = -√3/2,
tan150° = -1/√3

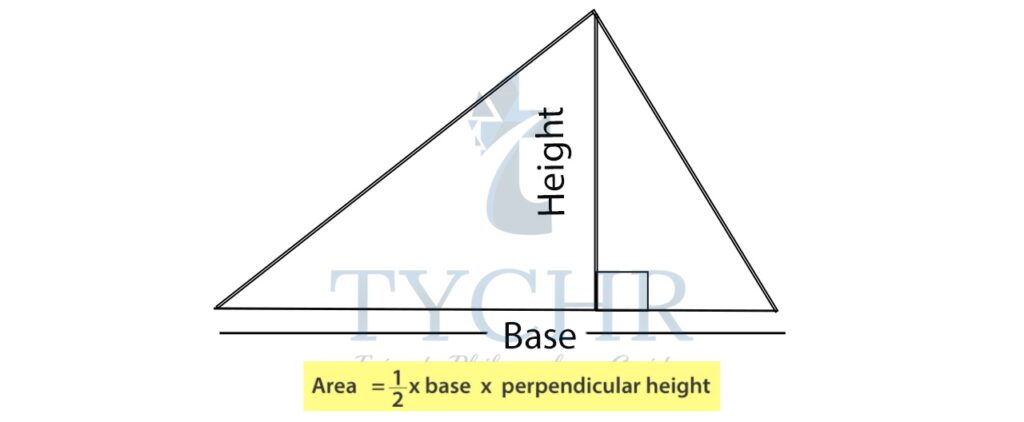
AREAS OF TRIANGLE

We are familiar with the area of triangle, if the base and the height perpendicular to the base is given:

Now, consider the following diagram:

The value of sin⁡C from the right-angled triangle BDC:
sinC = h/a
h = a sinC

We know that the area of triangle is (1/2)bh 
Replacing the value of h:
Area = (1/2) ab sinC

This formula allows you to find the area of a triangle where you do not have a right angle but do have two sides and the angle between them (the included angle).

(1/2)ab sinC = (1/2)bc sinA = (1/2) ac sinB 

This formula is applicable even when the angle between the given 2 sides is obtuse.
(sin⁡(180-θ)=sin⁡(θ)
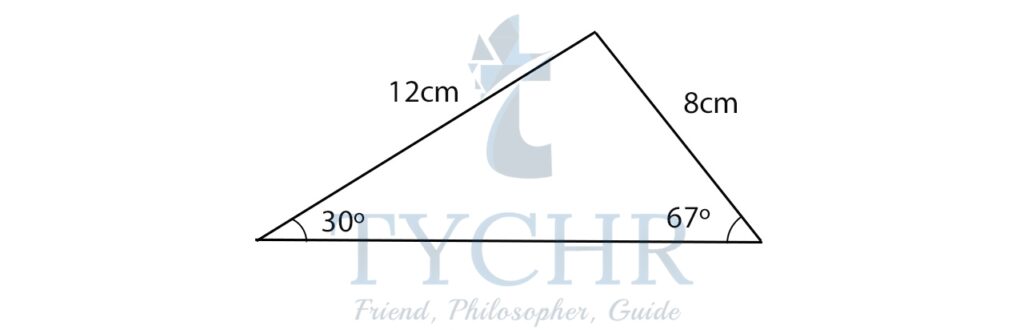
Ex. Find the area of the given triangle:

The sum of all angles of a triangle is 180°.
Let the angle included between the given sides be x.
30+67+x=180
x=83°

The area will be- (1/2)x12x8x sin 83° 
Area=47.64 cm2

EQUATIONS OF LINES AND ANGLES BETWEEN TWO LINES

Angle between a line and the x-axis:
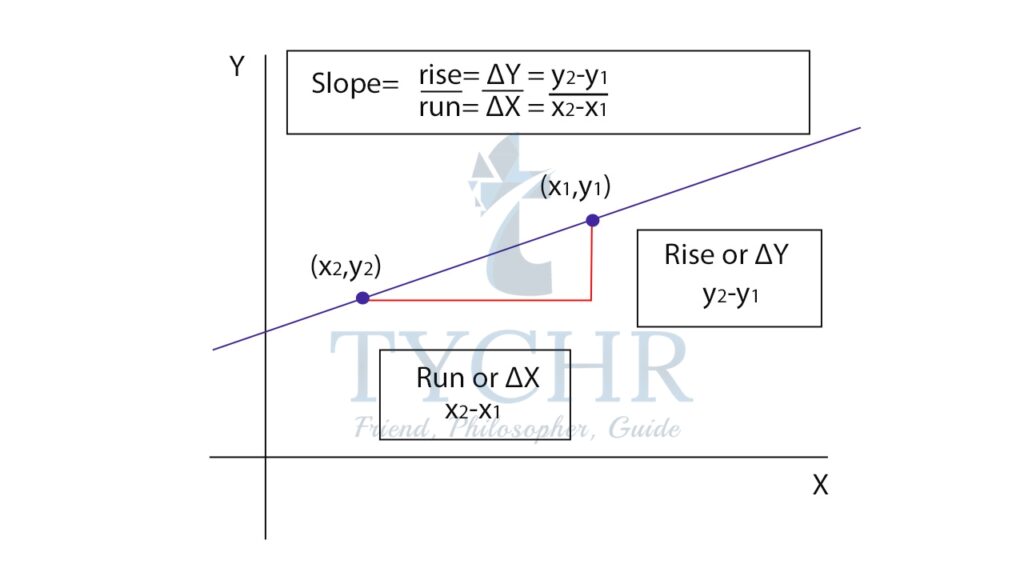
We are familiar with the equations of line in different forms. We know that the slope m of a line is given by – 𝑚 = 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑐ℎ𝑎𝑛𝑔𝑒/ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙 𝑐ℎ𝑎𝑛𝑔𝑒 = (𝑦₂−𝑦₁)/(𝑥₂−𝑥₁) , where (x₁,y₁) and (x₂,y₂) are points on the line.

Now observe there is a right-angled triangle formed.
We know that tan 𝜃 = 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑠𝑖𝑑𝑒/𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑠𝑖𝑑𝑒 = ∆𝑦/∆𝑥 = (𝑦₂−𝑦₁)(𝑥₂−𝑥₁)= m
Therefore, the angle between the x-axis and the line will be θ=tan^(-1)⁡m

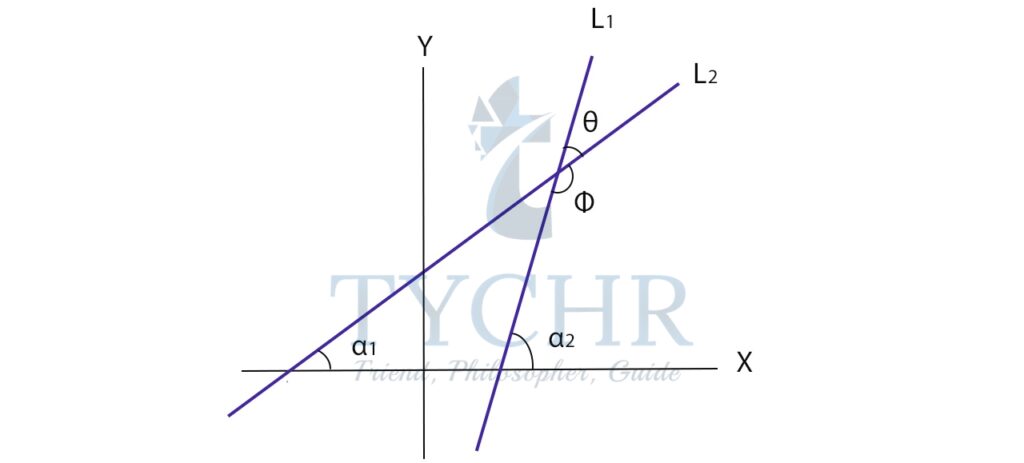
Angle between two lines:

There is a acute and a obtuse angle between two lines, which evidently sums up to 1800. When asked for an angle between 2 lines, the convention is to give the acute angle.
The acute angle is θ and the obtuse angle is ∅.
The angle between the first line and the x-axis is α₁
The angle between the second line and the x-axis is α₂

Applying exterior angle property of triangle:
α₁=α₂+θ
θ=α₁-α₂

In general, the angle between 2 lines will be:
θ=|α₁-α₂ |

Ex. Find the acute angle between the lines y=5x-3 and y= (1/2)x -4y
The angle between y=5x-3 and the x-axis will be α₁=tan^-1⁡5=78.690
The angle between y = (1/2)x – 4 and the x-axis will be α₂=tan^-1⁡(1/2)=26.565

The angle between the lines will be θ=|α₁-α₂|=|78.690-26.565|
θ=52.1249

THE SINE RULE AND THE COSINE  RULE

The sine and cosine rules are used to find unknowns of a triangle which is not right-angled.

THE SINE RULE

We know that the area of a triangle is given by:
1/2 ab sin⁡C=1/2 bc sin⁡A=1/2 ac sin⁡B
Dividing each term by 1/2 ab: sinC/c = sinA/a = sinB/b Rearranging:

sinA/a = sinB/b = sinC/c The sine rule is used when:
Two angles and one side is given
Two sides and a non-included angle is given

THE COSINE RULE

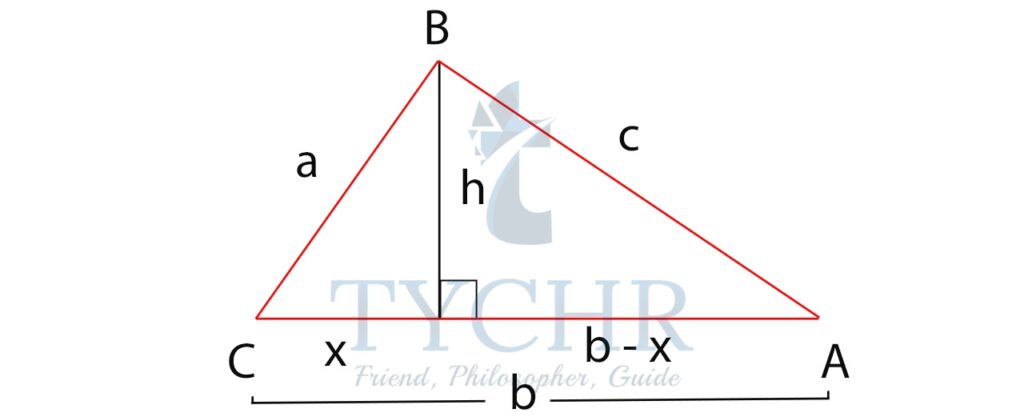
Applying pythagorus theorem to triangle ABD
c² = h² + (b-x)²
c² = h² + b² + x² – 2bx    ①

Applying pythagorus theorem to triangle CBD
a² = h² + x²  ②

Subtracting equation ② from ①:
c² – a² = b ²-2bx
2bx = a² + b² – c²
x = (a² + b² + c² )/2b

Now, from triangle ABD:
cosA = (b-x)/c
Putting the value of x: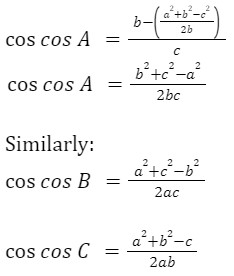The cosine rule is used when:

Three sides are given
Two sides and the included angle are given

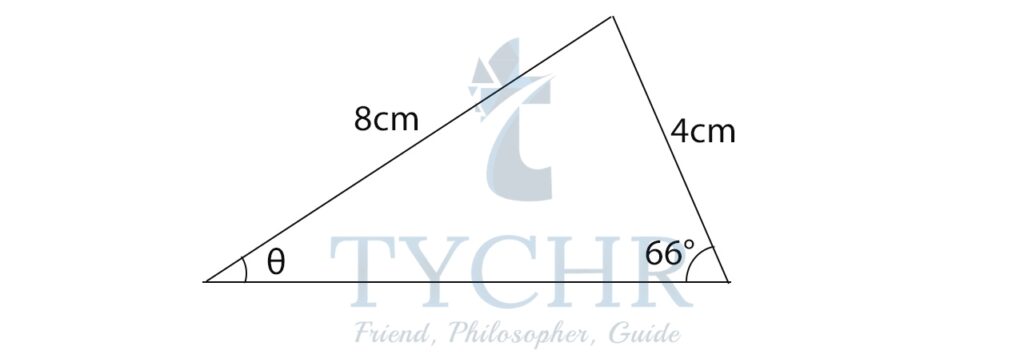
Ex. Find the value of θ:

Applying sine rule:
sin66°/8 = sinθ/4
Using GDC:
θ=27.1790

Ex. Find x:

Applying sine rule:
sin33°/x = sin108°/24
Using GDC:
x=13.744

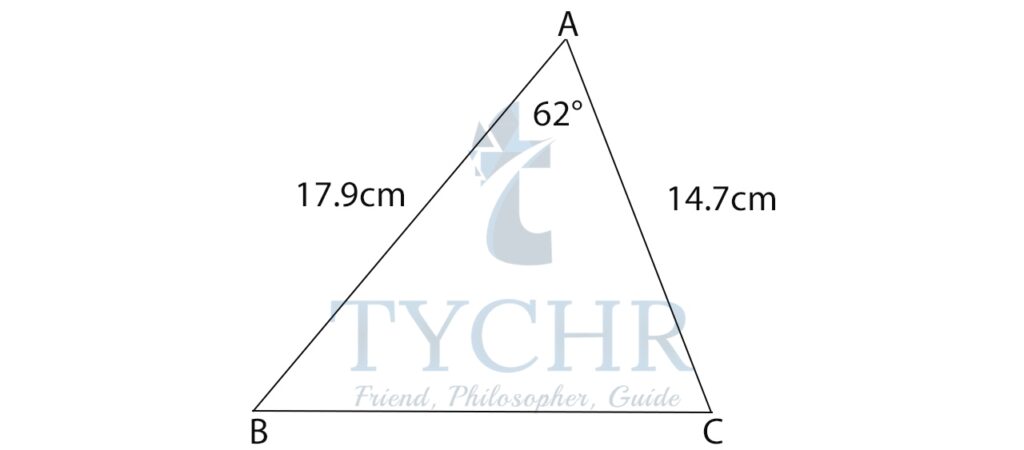
Ex. Find BC
BC=a, AB=c, AC=b
Applying cosine rule:
cosA = (b² + c² – a² )/2bc
cos62°= ((14.7)² + (17.9)² – a²)/(2(14.7)(17.9))
536.5-a²=247.06
a²=289.43
a=17.012
BC=17.012 cm

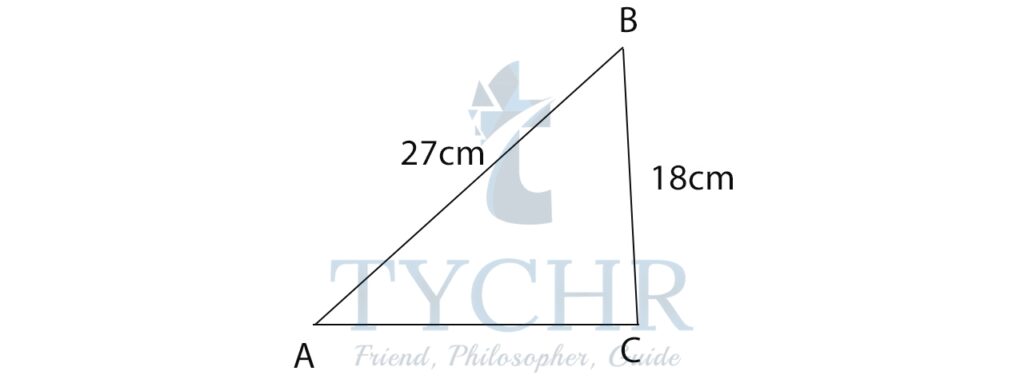
Ex. Find angle A

AB=c=27 cm
BC=a=18 cm
AC=b=21 cm
Using cosine rule:
cosA = (b² + c² – a² )/2bc
cosA = (21² + 27² – 18² )/2(21)(27)
cos⁡A=0.746
A=41.75°