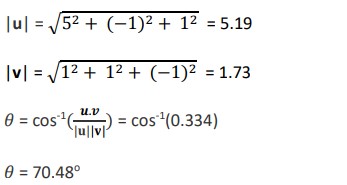By the end of this chapter you should be familiar with:

• Vector quantities
• Determining the vector equations of lines
• Kinematic models
• Scalar and vector products
• Angle between vectors in 3-D space

Scalar is a quantity which only has magnitude but a vector has both magnitude and direction.

VECTOR REPRESNTATION

You can represent vectors by drawing them. When a vector is represented graphically, its magnitude is represented by the length of an arrow and its direction is represented by the direction of the arrow. Here is an example:

Any vector w can be represented by an arrow.
A second arrow with the same magnitude that points in the opposite direction is -w.
Another arrow n times the magnitude and in the same direction would be represented as nw.
In 3-D space, the unit vectors along x, y and z axes are 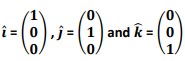 respectively. They are also known as base vectors.

VECTOR ADDITION AND SCALAR MULTIPLICATION

Addition and multiplication are done the same way as complex numbers.
When scalars and their scalar multiples are combined, the result is called a linear combination.
Let’s take an example to recall how addition and scalar multiplication was done for complex numbers.

Example: Let vector u = -3i + 5j +2k and v = i – 2k. Find vector component w when w = u – 2v

Solution: w = -3i +5j +2k -2(i – 2k) = -5i + 5j +6k

UNIT VECTORS

Unit vectors have a magnitude of 1. They are represented by 𝒗̂= v/|v| where |v| represents the magnitude of vector v.

Example: Find the unit vector p for the given vector, 12i – 3j – 4k.
Solution: Let’s find the magnitude of p,
|p| = √𝑎² + 𝑏² + 𝑐² = √12² + 3² + 4² = 13
Let’s use this magnitude to find the unit vector now:
𝑝̂= p/|p| = (12i – 3j – 4k)/13 = (12𝑖/13) − (3𝑗/13) − (4𝑘/13)

VECTOR AND PARAMETRIC EQUATIONS OF LINES

Lets consider the gradient to be equal q/p where for every non-zero p units in the x-direction, the line changes by q units in the y-direction. The gradient can also be written as m = p i ̂ + q j ̂ and the line has a y-intercept passing through the point (0,b).
Using y = mx + c,
y = (𝑞/𝑝) x + b
𝑥−0/𝑝 = 𝑦−𝑏/𝑞
Therefore, the equation of lines is:
𝑥−𝑥₀/𝑝=𝑦−𝑦₀/𝑞

For 3-D the equation would be, 𝑥−𝑥₀/𝑝=𝑦−𝑦₀/𝑞 = z−z₀/z
where m = p 𝒊̂+ q 𝒋̂+ s 𝒌̂

Example: Find the equation of A(-5,2) with m = 2/3

Solution: Using 𝑥−𝑥₀/𝑝=𝑦−𝑦₀/𝑞
(x + 5)/3 = (y-2)/2
2x – 3y + 16 = 0

The position vector of a point P, with coordinates (x, y, z), is the vector 𝑟⃗ with initial point on the origin and terminal point on P.
𝑟⃗ = x i + y j+ z k

Parametric form of an equation is given by:

k = 𝑥−𝑥₀/𝑝=𝑦−𝑦₀/𝑞 = z−z₀/z where k is a constant.

KINEMATICS

VELOCITY AND ACCELERATION VECTORS

The trajectory of a moving point can be determined at every moment t by an expression for the position vector of the point as a function of time.

𝑟⃗ = x(t) i + y(t) j+ z(t) k

Each of the three components x(t), y(t) and z(t) is a function of time. In a time interval ∆t = t2 – t1 the displacement of the point is equal to
∆𝑟̂ = 𝑟⃗₂− 𝑟⃗₁  where r2 and r1 are position vectors

If the velocity vector, v = x i + y j+ z k
then the acceleration vector, a = dv/dt

Example: A particle has velocity v(t) where v = (4t – 6)i – (3t)j. Find:

1. The speed of the particle when t = 3
2. Find the time at which the direction of movement of the particle is parallel to j
3. Find the acceleration

Solution:

1. For t = 3, v = 6i – 9j
   Speed = √36 + 81 = 10.81 ms^-1
2. 4t – 6 =0
   t = 1.5
3. a = dv/dt
   a = 4i – 3j

MINIMUM DISTANCE

From the previous chapters as we already know how to calculate distance. The distance between a point and an object in motion can be considered as two points and subtracted to get the distance as:

AB| = √(𝒂_𝟏 − 𝒃_𝟏)^𝟐 + (𝒂_𝟐 − 𝒃_𝟐)^𝟐 + (𝒂_𝟑 − 𝒃_𝟑)^𝟐

Then we’ll get a quadratic equation ax² + bx + c where
Minimum distance = c – (b^𝟐/4a) when t = (-b/2a) = 6/2 = 3
We can do the same with two objects in motion. Lets take an example to understand this better.
This minimum distance is known as displacement.

Example: A drone starts at point A(0,0,0) and flies a constant velocity along the vector u = 6i + 8j +2k each second, while another drone, already hovering at the point B(24,12,18) starts to descend at the same point at v = -2i + 4j – 4k. Find the minimum distance between the drones.

Solution: The position of the first drone can be indicated by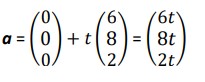
Similarly, the second one is indicated by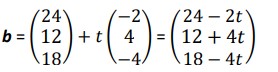

|AB| = √(𝑎₁ − 𝑏₁)² + (𝑎₂ − 𝑏₂)² + (𝑎₃ − 𝑏₃)²
= √(24 − 8𝑡)² + (12 − 4𝑡)² + (18 − 6𝑡)²
= √116(𝑡² − 6𝑡 + 9)

Minimum distance = c- (b²/4a) = 9 – 9 = 0
when t = (-b/2a) = 6/2 = 3

The drones will crash at t = 3 sec as the distance between them is 0.

SCALAR AND VECTOR PRODEUCTS

Scalar product or dot product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number.

If u = ai + bj + ck and v = di + ej +fk then u.v = ad + bf + cf
u.v = |u||v| cosθ

The work done by any force is the dot product of force and displacement W = F.D
Vector product or cross product is a binary operation on two vectors in three-dimensional space.
If u = ai + bj + ck and v = di + ej +fk then 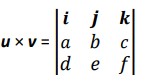u × v = |u||v| sinθ

The area could be found using cross product.
Angle between two vectors can also be found using dot product and cross product. It wouldn’t matter if we used dot product or cross product because you would get the same angle.

Example 1: Find the area of a parallelogram defined by coordinates (0,0,0), (1,3,4) and (2,1,3)

Solution: u = i + 3j + 4k and v = 2i + j + 3k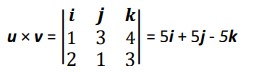
Area = √5² + 5² + (−5)² = 8.7 m²

Example 2: Find the angle between two vectors 5i – j + k and i + j – k

Solution: u = 5i – j + k and v = i + j – k
u.v = 5 – 1 – 1 = 3