IB Math AA SL Paper 1 Question Bank
The IB Math AA SL Paper 1 Question Bank is a great resource for students who are preparing for the IB Math AA SL exam. The Question Bank contains a wide variety of questions that cover all of the topics on the exam, and it is a great way to get extra practice before the big day. The Question Bank is also a great way to see how other students have tackled the same problems, and it can give you some insight into different approaches to solving problems.
Section A
1.) A ball is thrown vertically upwards from the top of a building 80 meters tall. The height of the ball above the ground, in meters, after t seconds is given by the function h(t) = 80 + 20t – 5t2.
a) Write down the equation of the motion of the ball in the form of h(t) = v0t + 1/2at2
The equation of motion is already given in the form of h(t) = v0t + 1/2at2 with v0 = 20 m/s and a = -5 m/s2
b) At what time will the ball reach its maximum height?
To find the time at which the ball reaches its maximum height, we need to find the time at which the ball’s velocity is zero. The ball’s velocity is given by the first derivative of the height function, h'(t) = 20 – 10t. Setting this equal to zero and solving for t gives
0 = 20 – 10t, t = 2s
so, after 2s the velocity will be zero and thus the ball has reached its max height
c) How high is the maximum height?
To find the maximum height, we substitute the value of t = 2 into the height function:
h(2) = 80 + 20(2) – 5(2)2 = 80 + 40 – 20 = 100m
so the maximum height of the ball is 100 meters.
2.) The function f(x) = 3x2 – x3 is defined on the interval [-1, 1].
a) Find the x-coordinates of any stationary points of f(x)
To find the x-coordinates of any stationary points of f(x), we take the derivative of the function and set it equal to zero:
f'(x) = 6x – 3x2 = 3x(2-x) = 0
Solving for x, we get:
x = 0 or x = 2
Thus, the x-coordinate of the stationary points of f(x) is x = 0 and x = 2
b) Determine the nature of the stationary points found in part (a).
To determine the nature of the stationary points, we need to take the second derivative of the function and test it at the x-coordinates of the stationary points:
f”(x) = 6 – 6x
When x = 0, f”(x) = 6 >0 which indicate a Minimum Point
When x = 2, f”(x) = -6 < 0 which indicate a Maximum Point
c) Find the y-coordinate of the stationary point found in part (a)
To find the y-coordinate of the stationary point found in part (a), we substitute the value of x = 0 into the function:
f(0) = 3(0)2 – (0)3 = 0
So, the y-coordinate of the stationary point is (0,0)
So, this is a Minimum Point and at (0,0)
3.) Use the sine rule to find the size of side a.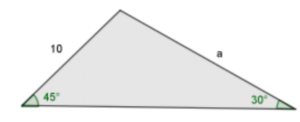
Using sineA/a = sinB/b
a= (10sin45°)/sin30° = 10√2
4.) Consider the quadratic 4x2 – 120x + 800
a)Solve the following
i) Find the roots.
x=10, x=20
ii) Hence express the quadratic in the form y= a(x-x1)(x-x2)
y= 4(x-10)(x-20)
b) Solve the following
i) Find the coordinates of the vertex.
(15,-100)
ii) Hence express the quadratic in the form y= a(x-h)2+k
y= 4(x-15)2-100
iii) Write down the equation of the axis of symmetry
x=15
iv) Write down the minimum value of y
Ymin= -100
c) Write down the y-intercept of the quadratic
y=800
5.) Let g(x) = 2x sinx
a)Find g’(x)
g’(x) = 2sinx + 2xcosx
b) Find the gradient of the graph where x= π
g’(π) = 2sinπ +2πcosπ = -2π
6.) Solve the equations
a) logx + log(x+1) = log6
Using property: log(A) +log(B) = log( AB)
x(x+1)=6
x2+x-6=0
x=2
b) logx + log(x+3) = 10
Using property: log(A) +log(B) = log( AB)
x(x+3)=10
x2+3x-10=0
x=2
c) log(x+18) – logx = 1
Using property: log(A) -log(B) = log( A/B)
(x+18)/x= 1
Section B
7.) Let f(x) = x4 – 4x3 + 3x2 + 2x – 1.
a) Find the equation of the tangent line to the graph of y = f(x) at the point (1, -2).
To find the equation of the tangent line at a point (a, f(a)) on the graph of y = f(x), we need to use the following equation: y = f(a) + f'(a)(x – a).
Where f'(a) is the derivative of f(x) evaluated at x = a.
First, we find the derivative of f(x) which is:
f'(x) = 4x3 – 12x2 + 6x + 2
Now we substitute a = 1 into f'(a) to get f'(1) = 4(1)3 – 12(1)2 + 6(1) + 2 = -6
Therefore, the equation of the tangent line at (1, -2) is:
y = -2 + (-6)(x – 1)
y = -2 – 6x + 6
y = -6x + 8
b) Find the equation of the normal to the graph of y = f(x) at the point (1, -2).
To find the equation of the normal line at a point (a, f(a)), we need to use the following equation: y – f(a) = -1/f'(a)(x – a)
We know that f'(1) = -6 from part (a)
Therefore, the equation of the normal line at (1, -2) is:
y + 2 = 1/6(x – 1)
y = 1/6x – 1/3
c) Find the coordinates of the point of intersection of the tangent line and the normal to the graph of y = f(x) at the point (1, -2).
To find the coordinates of the point of intersection of the tangent line and the normal line, we need to solve the system of equations formed by the equations of the tangent line and normal line.
By substituting the equation of the normal line into the equation of the tangent line, we get:
-6x + 8 = 1/6x – 1/3
Solving this equation for x, we get:
x = 3/2
Now we can substitute this value into either of the equations of the tangent line or normal line to find the y-coordinate.
By substituting x = 3/2 into the equation of the tangent line, we get
y = -6x + 8 = -6(3/2) + 8 = -9/2 + 8 = -1/2
Therefore, the point of intersection of the tangent line and the normal line at (1, -2) is (3/2, -1/2)
d) Find the x-intercepts of the graph of f(x).
To find the x-intercepts of the graph of f(x), we set f(x) = 0 and solve for x:
x4 – 4x3 + 3x2 + 2x – 1 = 0
This equation can be factored as:
(x – 1)(x – 1)(x + 1)(x – 1) = 0
Therefore, the x-intercepts are x = 1 (with multiplicity 3) and x = -1.
e) Find the y-intercept of the graph of f(x).
To find the y-intercept of the graph of f(x), we set x = 0:
f(0) = 0 – 4(0) + 3(0) + 2(0) – 1 = -1
Therefore, the y-intercept is (0, -1).
f) Find the critical points of f(x) and classify them as local maximums, local minimums, or points of inflection.
f'(x) = 4x3 – 12x2 + 6x + 2
f”(x) = 12x2 – 24x + 6
Setting f'(x) = 0, we get:
4x3 – 12x2 + 6x + 2 = 0
This equation can be simplified by dividing both sides by 2:
2x3 – 6x2 + 3x + 1 = 0
We can use synthetic division to factor this equation as:
(x – 1)(2x2 – 4x – 1) = 0
Therefore, the critical points are x = 1, x = (2 + sqrt(6))/2, and x = (2 – sqrt(6))/2.
To classify the critical points, we use the second derivative test. For x = (2 + sqrt(6))/2, we have:
f”((2 + sqrt(6))/2) = 12((2 + sqrt(6))/2)2 – 24((2 + sqrt(6))/2) + 6 = -11 – 6sqrt(6) < 0
Therefore, x = (2 + sqrt(6))/2 is a local maximum. For x = (2 – sqrt(6))/2, we have:
f”((2 – sqrt(6))/2) = 12((2 – sqrt(6))/2)2 – 24((2 – sqrt(6))/2) + 6 = -11 + 6sqrt(6) > 0
Therefore, x = (2 – sqrt(6))/2 is a local minimum. For x = 1, we have:
f”(1) = 12(1)2 – 24(1) + 6 = -6 < 0
Therefore, x = 1 is a point of inflection.
g) Sketch the graph of f(x) for -2 ≤ x ≤ 3, clearly indicating any intercepts, critical points, and asymptotes.
To sketch the graph of f(x) for -2 ≤ x ≤ 3, we use the information we have gathered in parts (a)-(c).
First, we plot the x-intercepts, which are x = -1 (with multiplicity 1) and x = 1 (with multiplicity 3). We also plot the y-intercept, which is (0, -1).
Next, we plot the critical points, which are x = 1 (a point of inflection), x = (2 + sqrt(6))/2 (a local maximum), and x = (2 – sqrt(6))/2 (a local minimum).
To determine the behavior of the graph between the critical points, we can use the first and second derivatives of f(x). Note that f”(x) is positive to the left of x = (2 – sqrt(6))/2 and to the right of x = (2 + sqrt(6))/2, and negative between these two points. This means that f'(x) is increasing to the left of x = (2 – sqrt(6))/2 and to the right of x = (2 + sqrt(6))/2, and decreasing between these two points.
Using this information, we can sketch the graph of f(x) as follows:
- To the left of x = (2 – sqrt(6))/2, the graph is increasing and concave up.
- At x = (2 – sqrt(6))/2, there is a local minimum.
- Between x = (2 – sqrt(6))/2 and x = 1, the graph is decreasing and concave up.
- At x = 1, there is a point of inflection.
- Between x = 1 and x = (2 + sqrt(6))/2, the graph is decreasing and concave down.
- At x = (2 + sqrt(6))/2, there is a local maximum.
To the right of x = (2 + sqrt(6))/2, the graph is increasing and concave down.
.
. .
. .
. .
. .
. .
. .
. .
————————————-
-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3
8.) A company produces two types of smartphones: Type A and Type B. The company conducted a survey of 2000 smartphone users to determine their preference. The results of the survey are summarized in the following table:
Type A |
Type B |
|
Prefer Type A |
1300 |
200 |
Prefer Type B |
300 |
200 |
No Preference |
100 |
100 |
a) Find the probability that a randomly chosen smartphone user prefers Type A.
The probability that a randomly chosen smartphone user prefers Type A is (1300 + 200)/2000 = 0.75.
b) Given that a smartphone user prefers Type B, what is the probability that the user has no preference for Type A or B?
The probability that a smartphone user has no preference for Type A or B, given that they prefer Type B, is 100/500 = 0.2. This is because out of the 500 people who prefer Type B, 100 have no preference for Type A or B.
c) A smartphone user is selected at random. Find the probability that the user prefers Type A or has no preference for Type A or B.
The probability that a smartphone user prefers Type A or has no preference for Type A or B is the sum of the probabilities of these two events. From part (a), the probability that a smartphone user prefers Type A is 0.75. From the table, the probability that a smartphone user has no preference for Type A or B is (100 + 100)/2000 = 0.1. Therefore, the probability that a smartphone user prefers Type A or has no preference for Type A or B is 0.75 + 0.1 = 0.85.
d) The company randomly selects 10 smartphone users to participate in a focus group. What is the probability that exactly 6 of the users prefer Type A?
The number of ways to select exactly 6 people who prefer Type A out of 10 people is given by the binomial coefficient (10 choose 6), which is 210. The probability of each such outcome is (1300/2000)6 x (700/2000)4, since the probability that a person prefers Type A is 1300/2000 and the probability that a person prefers Type B or has no preference is (200 + 100 + 200 + 100)/2000 = 0.7. Therefore, the probability of selecting exactly 6 people who prefer Type A is 210 x (1300/2000)6 x (700/2000)4 = 0.139.
e) Based on the survey results, can the company claim that a majority of smartphone users prefer Type A over Type B at a significance level of 0.05? Justify your answer.
We can use a two-sample proportion z-test to determine if the proportion of smartphone users who prefer Type A is significantly different from the proportion who prefer Type B or have no preference. Let p1 be the proportion of smartphone users who prefer Type A and p2 be the proportion who prefer Type B or have no preference. Then:
p1 = 1300/2000 = 0.65
p2 = (200 + 100 + 200 + 100)/2000 = 0.35
The null hypothesis is that p1 = p2, and the alternative hypothesis is that p1 ≠ p2. We can use a significance level of 0.05.
The test statistic is given by:
z = (p1 – p2) / sqrt(p̂(1 – p̂) (1/n1 + 1/n2))
where p̂ is the pooled proportion, given by:
p̂ = (x1 + x2) / (n1 + n2)
and x1 and x2 are the numbers of smartphone users who prefer Type A and Type B or have no preference, respectively.
From part (a), n1 = 2000 and n2 = 500. From the table, x2 = 400. Therefore, x1 = 1300 and p̂ = (1300 + 400) / (2000 + 500) = 0.65.
Substituting these values into the formula for the test statistic, we get:
z = (0.65 – 0.35) / sqrt(0.5 x 0.5 x (1/2000 + 1/500)) = 12.81
Using a standard normal distribution table, we can find that the p-value is very small (less than 0.0001). Therefore, we reject the null hypothesis and conclude that the proportion of smartphone users who prefer Type A is significantly different from the proportion who prefer Type B or have no preference at a significance level of 0.05.
9.) Let f(x) = x3 – 9x2 + 24x + 1.
a) Find the first derivative of f(x).
The first derivative of f(x) is:
f'(x) = 3x2 – 18x + 24
b) Determine the x-coordinates of the critical points of f(x).
To find the critical points of f(x), we need to set f'(x) equal to zero and solve for x:
3x2 – 18x + 24 = 0
x2 – 6x + 8 = 0
(x – 2)(x – 4) = 0
x = 2 or x = 4
Therefore, the critical points of f(x) are x = 2 and x = 4.
c) Determine the intervals on which f(x) is increasing and decreasing.
To determine the intervals on which f(x) is increasing and decreasing, we need to look at the sign of the first derivative:
f'(x) = 3x2 – 18x + 24
On the interval (-∞, 2), f'(x) is negative, so f(x) is decreasing.
On the interval (2, 4), f'(x) is positive, so f(x) is increasing.
On the interval (4, ∞), f'(x) is positive, so f(x) is increasing.
Therefore, f(x) is decreasing on the interval (-∞, 2) and increasing on the intervals (2, 4) and (4, ∞).
d) Determine the x-coordinate(s) of the local maximum and minimum point(s) of f(x).
To find the local maximum and minimum points of f(x), we need to examine the sign of the second derivative:
f”(x) = 6x – 18
At x = 2, f”(x) is negative, so there is a local maximum at x = 2.
At x = 4, f”(x) is positive, so there is a local minimum at x = 4.
Therefore, the local maximum point of f(x) is (2, 19) and the local minimum point of f(x) is (4, -7).
e) Find the second derivative of f(x).
The second derivative of f(x) is:
f”(x) = 6x – 18
f) Determine the intervals on which f(x) is concave up and concave down.
To determine the intervals on which f(x) is concave up and concave down, we need to look at the sign of the second derivative:
f”(x) = 6x – 18
On the interval (-∞, 3), f”(x) is negative, so f(x) is concave down.
On the interval (3, ∞), f”(x) is positive, so f(x) is concave up.
Therefore, f(x) is concave down on the interval (-∞, 3) and concave up on the interval (3, ∞).
g) Determine the x-coordinate(s) of the inflection point(s) of f(x).
To find the inflection points of f(x), we need to set f”(x) equal to zero and solve for x:
6x – 18 = 0
x = 3
Therefore, the inflection point of f(x) is (3, -16).
Our Expert Tutors!
- 12+ Years
Cat 1 – ESS and Cat 2 – Biology. Chief of the IB program. Mentored 320+ students across various curricula.
- 24+ Years
IBDP Physics HL / SL. IGCSE Physics. A-level Physics (AQA, CIE, Edexcel, OCR, and WJEC). IGCSE Physics (AQA,CIE, OCR & Edexcel)
- 9+ Years
IBDP Cat 1 – Business Management, IBDP Cat 1 – TOK. Taught over 130+ students across 4+ countries.
- 9+ Years
IBDP Cat 1 & 2 November 2019. Specializes in Global Politics. Many students scored 7s; mentors 200+ students in assessments.
- 16+ Years
Specializing in Mathematics: Analysis and Approaches (HL & SL), Mathematics: Applications and Interpretation (HL & SL), and MYP (Mathematics).
- 18 + Years
IBDP Cat 1 – Chemistry, IBDP Cat 3 – IA Chemistry, IBDP Cat 1 – TOK. Helped 2 out of 3 students achieve a 7 in IB Chemistry.












