IB Math AA SL Paper 2 Question Bank

If you’re looking for an IB Math AA SL Paper 2 Question Bank, you’ve come to the right place! We have a wide selection of questions available, covering all of the topics you’ll need to know for your exam. Whether you’re needing help with geometry or statistics, we’ve got you covered. With our question bank, you’ll be able to work through practice problems at your own pace and master the material before test day. So why wait? Get started today and ace that paper 2!

Section A

1.) A rectangular prism has a volume of 48 cubic meters and a square base with a side length of 2 meters. The height of the prism is h meters.

a) Express the total surface area of the rectangular prism as a function of h.
We know that the volume of a rectangular prism is given by V = lwh, where l, w and h are the length, width and height of the prism respectively. In this case, we know that V = 48 m³ and the side length of the base is 2 m.

Therefore, the width and length of the base are both 2 m. So, we can express the volume as
V = 2w * 2l * h = 48 m³

We know the formula for the surface area of a rectangular prism is 2lw+ 2lh + 2wh. Here we know width w = l = 2m and h is the variable.

So, the surface area A of the rectangular prism as a function of h is:
A = 2 * 2 * 2 + 2 * 2 * h = 8 + 4h

b) Express the height h of the rectangular prism as a function of the total surface area.
To express the height h as a function of the total surface area, we can use the surface area equation that we found in part a. If we let A be the total surface area, then:
A = 8 + 4h

Rearranging this equation to solve for h gives us:
h = (A-8)/4

So, h is a function of the total surface area.
The surface area as a function of h is A = 8+ 4h, and the h as a function of the surface area is h = (A-8)/4

2.) An amount of $ 10 000 is invested at an annual interest rate of 12%.

a) Find the value of the investment after 5 years

i) if the interest rate is compounded yearly;
FV=10000(1+12/100)ⁿ
n= 5, 17623.42

ii) if the interest rate is compounded half-yearly;
n= 10, 17908.48

iii) if the interest rate is compounded quarterly;
n=20, 18061.11

iv) if the interest rate is compounded monthly.
n= 5*12, 18166.97

b) The value of the investment will exceed $ 20 000 after n full years. Calculate the minimum value of n

i) if the interest rate is compounded yearly;
20000= 10000(1+12/100)ⁿ
Solve by GDC
n=6.11, hence n=7

ii) if the interest rate is compounded monthly.
20000= 10000(1+12/100)¹²ⁿ
Solve by GDC
n=5.81, hence n=6

3.) A car rental company charges a fixed daily rental fee of $50, and a variable charge of $0.15 per kilometre driven.

a) Write an expression for the cost of renting the car for d days, and traveling x kilometers.
The cost of renting the car is made up of two parts: a fixed daily rental fee and a variable charge per kilometer driven. To find the total cost, we need to multiply the number of days the car is rented by the daily rental fee, and add that to the product of the number of kilometers driven and the variable charge per kilometer.

So, the total cost, C, can be expressed as an equation:
C = d * 50 + x * 0.15

b) The company offers a weekly rental package for $400, which includes a maximum of 600km of travel. Express the cost of the weekly rental package, C, in terms of the number of kilometres driven, x.
To find the cost of the weekly rental package in terms of the number of kilometers driven, we know that the package includes 600km of travel and cost $400. So we can create an equation:
C = 400 = d * 50 + x * 0.15

we know that d = 7 for a weekly package and x is 600km
So,
C(x) = 7 * 50 + x * 0.15 = 400
Hence C(x) = 7*50 + 0.15x = 400
this is the equation that expresses the cost of the weekly rental package, C, in terms of the number of kilometres driven, x.

4.) Triangle ABC is a right-angled triangle, with right angle at B and hypotenuse C.

a) Write down the value of sin B, cos B and tan B in terms of a and b.
In a right-angled triangle, we can use the trigonometric functions sine, cosine, and tangent to relate the lengths of the sides to the measure of the angles.
For a right-angled triangle,
sin B = a/c, cos B = b/c, tan B = a/b

b) If a = 5 and b = 12, find the values of sin B, cos B and tan B.
If we plug in the given values, a = 5 and b = 12, we can find the values of sin B, cos B and tan B:
sin B = a/c = 5/c
cos B = b/c = 12/c
tan B = a/b = 5/12

c) Use the result from part (b) to find the value of c.
To find the value of c, we can use the Pythagorean theorem, c = √(a² + b²) = √(5² + 12²) = √(25 + 144) = √(169) = 13

5.) Solve the following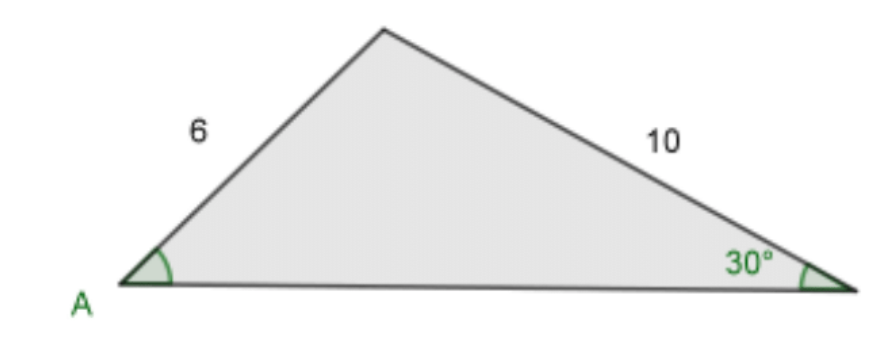

a) Use the sine rule to find the sine of the angle A
Sin A = (10sin30°)/6
Sin A= 5/6

b) Hence find the two possible values of angle A
A= 56.4° or A = 124°

6.) The weight X of a particular animal is normally distributed with μ= 200kg and σ= 15kg. An animal of this population is overweight if it has a weight greater than 230 kg

a) Find the probability that an animal is overweight.
P (X>230) = 0.02275

b) We select 2 animals from this population. Find the probabilities that

i) both animals are overweight
(0.02275)²= 0.000518

ii) only one animal is overweight.
0.02275)* (1-0.02275)* 2 = 0.0445

c) We select 7 animals from this population. Find the probability that exactly two of them are overweight.
Y follows B(n,p) with n = 7, p =0.02275
P(Y=2) = 0.00969

Download our Successful College Application Guide

Our Guide is written by counselors from Cambridge University for colleges like MIT and other Ivy League colleges.

To join our college counseling program, call at +918825012255

Section B

1.) A factory produces electronic components. The probability of a component is defective is 0.05.

a) What is the probability of producing exactly 3 defective components in a batch of 50 components?
This is a binomial probability distribution problem. The probability of producing exactly 3 defective components in a batch of 50 components is:
P(X = 3) = (50 choose 3) * (0.05)³ * (1-0.05)^(50-3) = 19600 * 0.05³ * 0.95⁴⁷ ≈ 0.09

b)What is the probability of producing at most 3 defective components in a batch of 50 components?
To find the probability of producing at most 3 defective components, we can use the cumulative distribution function of the binomial distribution. The probability of producing at most 3 defective components is:
P(X <= 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
P(X <= 3) = (50 choose 0) * (0.05)⁰ * (1-0.05)⁵⁰ + (50 choose 1) * (0.05)¹ * (1-0.05)⁴⁹ + (50 choose 2) * (0.05)² * (1-0.05)⁴⁸ + (50 choose 3) * (0.05)³ * (1-0.05)⁴⁷ ≈ 0.37

The factory produces 1000 components per day.

c) What is the probability of producing more than 45 defective components in a day?
The expected number of defective components produced per day is:
E(X) = λ = n * p = 1000 * 0.05 = 50
The probability of producing more than 45 defective components in a day is:
1 – P(X <= 45) = 1 – (e^(-50) * (50⁴⁵) / 45!) ≈ 0.02

d) What is the probability of producing less than 45 defective components in a day?
To find the probability of producing less than 45 defective components in a day, we can use the Poisson cumulative distribution function. The probability of producing less than 45 defective components in a day is:
P(X < 45) = (e^(-50) * (50⁴⁴) / 44!) ≈ 0.98

2.) A company produces and sells widgets. The revenue, R (in dollars), from selling x widgets per day is given by the function R(x) = 2x² + 50x. The cost, C (in dollars), of producing x widgets per day is given by the function C(x) = 0.5x² + 25x + 100.

a.) Find the profit function, P(x), in terms of x.
The profit, P(x), is calculated by subtracting the cost, C(x), from the revenue, R(x):
P(x) = R(x) – C(x)
Substituting the given functions for R(x) and C(x):
P(x) = (2x² + 50x) – (0.5x² + 25x + 100)
P(x) = 1.5x² + 25x – 100

b.) Find the value of x that maximizes the profit.
To find the value of x that maximizes the profit, we need to find the vertex of the quadratic function P(x) = 1.5x² + 25x – 100. The x-coordinate of the vertex is given by the formula x = -b/2a, where a and b are the coefficients of the x² and x terms, respectively.
In this case, a = 1.5 and b = 25, so substituting these values into the formula:
x = -25 / (2 * 1.5)
x = -25 / 3
So, the value of x that maximizes the profit is x = -25/3.

c.) Calculate the maximum profit.
To calculate the maximum profit, we can substitute the value of x = -25/3 into the profit function P(x) = 1.5x² + 25x – 100.
P(-25/3) = 1.5 * (-25/3)² + 25 * (-25/3) – 100
P(-25/3) = -975/3 + (-625/3) – 100
P(-25/3) = -1600/3 – 100
P(-25/3) = -1100/3
So, the maximum profit is -1100/3 dollars.

d.) Determine the range of values of x for which the company makes a profit.
The company makes a profit when the profit function P(x) is positive. To determine the range of values of x for which the company makes a profit, we need to find the values of x that satisfy the inequality P(x) > 0.
1.5x² + 25x – 100 > 0
We can solve this inequality by using quadratic techniques, such as factoring or the quadratic formula. Once we find the solutions for x, we can determine the range of values of x for which the inequality is true, and thus the range of values of x for which the company makes a profit.
To determine the range of values of x for which the company makes a profit, we need to solve the inequality 1.5x² + 25x – 100 > 0. Let’s use the quadratic formula to find the solutions for x:
1.5x² + 25x – 100 > 0
a = 1.5, b = 25, c = -100
x = (-b ± √(b² – 4ac)) / (2a)
x = (-25 ± √(25² – 4 * 1.5 * -100)) / (2 * 1.5)
x = (-25 ± √(625 + 1200)) / 3
x = (-25 ± √1825) / 3
Now we can determine the range of values of x for which the inequality is true. Since the coefficient of x² is positive (1.5 > 0), the parabola opens upwards, and the inequality is true for values of x outside of the solutions we found.
So, the range of values of x for which the company makes a profit is x < (-25 – √1825) / 3 or x > (-25 + √1825) / 3.

3.) Let f(x) = x³ – 3x² – 4x + 12. Solve the equation f(x) = 0.

a.) By first testing the values of f(1) and f(2), show that there is a root of f(x) = 0 between x = 1 and x = 2.
We have f(1) = 6 and f(2) = 2, so by the intermediate value theorem, there must be a root of f(x) = 0 between x = 1 and x = 2.

b.) Use synthetic division to factorize f(x) into a linear factor and a quadratic factor.
To factorize f(x) using synthetic division, we first guess a root, which could be a factor of the constant term (12) divided by a factor of the leading coefficient (1). One possibility is x = 3. Then we divide f(x) by (x – 3):
1 -3 -4 12
3 | 1 -3 -4 12
-3 0 -12
————
1 -6 -4 0
So we have f(x) = (x – 3)(x² – 6x – 4).

c.) Find the remaining roots of f(x) = 0, giving your answers correct to three decimal places.
To find the remaining roots of f(x) = 0, we need to solve the quadratic factor x2 – 6x – 4. Using the quadratic formula, we get:
x = [6 ± sqrt(6² + 4*4*1)] / 2
x = 3 ± sqrt(19)
Therefore, the roots of f(x) = 0 are approximately x = 3, x = 3 + sqrt(19), and x = 3 – sqrt(19).

d.) Sketch the graph of y = f(x), indicating the x-intercepts, y-intercept, turning points, and end behavior.
To sketch the graph of y = f(x), we first find the x-intercepts by solving f(x) = 0:
f(x) = x³ – 3x² – 4x + 12
f(x) = (x – 3)(x2 – 4x – 4)
x = 3 or x = 2 + sqrt(6) or x = 2 – sqrt(6)\
Next, we find the y-intercept by evaluating f(0) = -1. We also find the turning points by setting f'(x) = 0 and solving for x:
f'(x) = 3x² – 6x – 4
f'(x) = 3(x – 2)(x + 2)
x = 2 or x = -2
Finally, we can sketch the graph of y = f(x) as follows: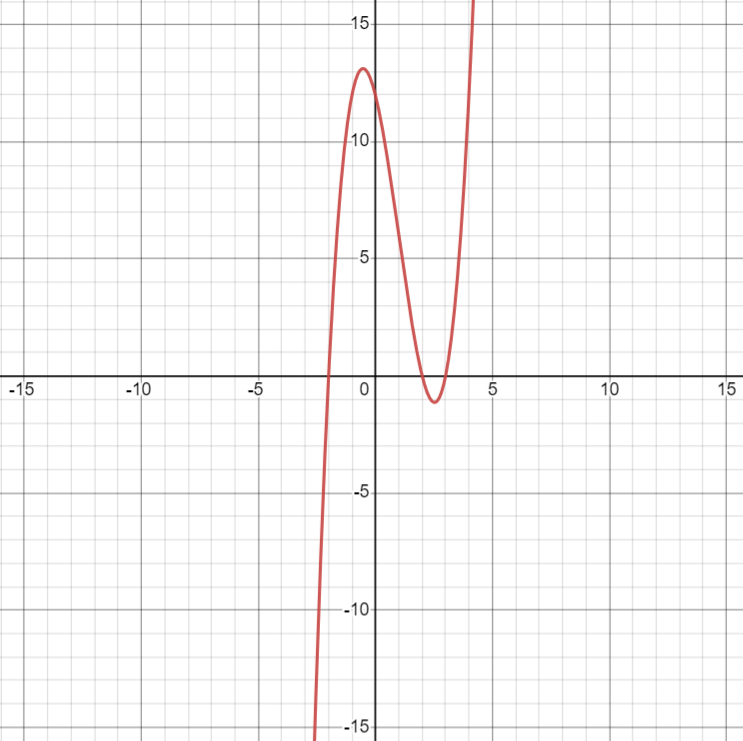

e.) Find the equation of the tangent line to the graph of y = f(x) at the point where x = 2.
To find the equation of the tangent line to the graph of y = f(x) at the point where x = 2, we first find the slope of the tangent line by taking the derivative of f(x) and evaluating it at x = 2:
f'(x) = 3x² – 6x – 4
f'(2) = 8
So the slope of the tangent line is 8. Next, we find the y-coordinate of the point of tangency by evaluating f(2) = 2:
f(2) = 2
Therefore, the equation of the tangent line to the graph of y = f(x) at the point where x = 2 is:
y – 2 = 8(x – 2)
y = 8x – 14

Our Expert Tutors!

Edit Template

Get access to our free IB resources

Edit Template