12.) O is the centre of the circle which has a radius of 5.4 cm.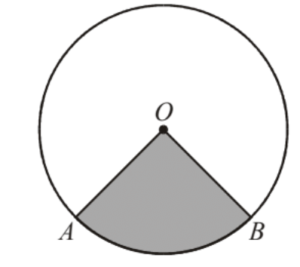

Area of the shaded sector OAB is 21.6 cm2. Find the length of the minor arc AB
½(5.4)2𝜃 = 21.6
𝜃 = 1.481 radians
AB = r𝜃 = 5.4*1.481 = 8cm

13.) The function f is defined by f(x) = x³ – 3x² + 2x + k, where k is a constant.

a) Find the stationary points of the function f, and determine whether each point is a maximum or minimum.
To find the stationary points of the function f, we need to find the values of x where the derivative of the function f(x) is equal to zero. Taking the derivative of f(x), we get:
f'(x) = 3x² – 6x + 2
Setting f'(x) equal to zero and solving for x, we get:
3x² – 6x + 2 = 0
Using the quadratic formula, we get:
x = (6 ± √24) / 6
Simplifying, we get:
x = 1 ± (1/√6)
Therefore, the two stationary points of the function f are:
x = 1 + (1/√6) and x = 1 – (1/√6)
To determine whether each point is a maximum or minimum, we can use the second derivative test. Taking the second derivative of f(x), we get:
f”(x) = 6x – 6
Evaluating f”(x) at each of the stationary points, we get:
f”(1 + (1/√6)) = 2(1 + (1/√6)) > 0, so this is a minimum.
f”(1 – (1/√6)) = 2(1 – (1/√6)) > 0, so this is also a minimum.
Therefore, the function f has two stationary points, both of which are local minima.

b) Find the range of values of k for which the function f(x) has no real roots.
To find the range of values of k for which the function f(x) has no real roots, we need to find the values of k for which the function f(x) is always positive or always negative. Since the function has two local minima, we know that it is negative to the left of the leftmost minimum and positive to the right of the rightmost minimum. Therefore, the function has no real roots if and only if the local minima are both positive. That is, we need to have:
f(1 + (1/√6)) > 0 and f(1 – (1/√6)) > 0
Substituting in the definition of f(x), we get:
(1 + (1/√6))³ – 3(1 + (1/√6))² + 2(1 + (1+ k > 0)

Simplifying, we get:
4 + (4/√6) + k > 0
Similarly, we need to have:
(1 – (1/√6))³ – 3(1 – (1/√6))² + 2(1 – (1/√6)) + k > 0
Simplifying, we get:
4 – (4/√6) + k > 0
Therefore, we need to have:
4 – (4/√6) < k < -(4/√6) – 4
So the range of values of k for which the function f(x) has no real roots is:
4 – (4/√6) < k < -(4/√6) – 4

14.) A man standing at point A on the bank of a straight river wants to reach point B on the opposite bank, which is directly opposite A. He can swim at a speed of 4 m/s, and the current in the river is 2 m/s. The width of the river is 200 m.

a) Find the time it takes the man to cross the river if he swims directly across.
If the man swims directly across the river, then his speed relative to the water is 4 m/s, and the distance he needs to swim is 200 m. Therefore, the time it takes him to cross the river is:
time = distance / speed = 200 / 4 = 50 seconds

b) Find the distance the man travels to reach point B if he swims directly across.
To find the distance the man travels to reach point B, we can use the Pythagorean theorem. Let D be the distance the man travels, and let x be the distance he is displaced downstream by the current. Then we have:
D² = (200 + x)² + 4²
Simplifying, we get:
D² = 200² + 2(200)(x) + x² + 16
Since x = (2 m/s) × (50 s) = 100 m, we can substitute this into the equation and simplify further:
D2 = 200² + 2(200)(100) + 100² + 16 = 40000 + 40000 + 10000 + 16 = 90016
Taking the square root of both sides, we get:
D = √90016 ≈ 300.02 m
Therefore, the man travels approximately 300.02 m to reach point B if he swims directly across the river.

c) Suppose the man swims at an angle θ to the direction of the current. Find an expression for the time it takes him to cross the river in terms of θ.
If the man swims at an angle θ to the direction of the current, then his speed relative to the water can be resolved into two components: one parallel to the current, which has speed 4 cos(θ), and one perpendicular to the current, which has speed 4 sin(θ). The distance he travels in the perpendicular direction is still 200 m, but the distance he travels in the parallel direction is now x = (2 m/s) × (50 s) cos(θ) = 100 cos(θ) m.
Therefore, the total distance the man travels is:
D² = (200 + 100 cos(θ))² + (200 sin(θ))²
Expanding and simplifying, we get:
D² = 40000 + 40000 cos²(θ) + 40000 cos(θ) + 10000 cos2(θ) + 40000 sin²(θ)
D² = 50000 + 40000 cos²(θ) + 40000 cos(θ) + 40000 sin²(θ)
D² = 90000 + 40000 cos(θ)
To find the time it takes the man to cross the river, we can divide the distance by the total speed, which is the magnitude of the velocity vector relative to the water:
time = D / √((4 cos(θ))² + (2 + 4 sin(θ))²)
Substituting in the expression we found for D, we get:
time = √(90000 + 40000 cos(θ)) / √((4 cos(θ))² + (2 + 4 sin(θ))²)

Simplifying the denominator, we get:
time = √(90000 + 40000 cos(θ)) / √(16 cos²(θ) + 16 sin²(θ) + 4 + 16 sin(θ) + 16 cos(θ))

Simplifying further, we get:
time = √(90000 + 40000 cos(θ)) / √(20 + 20 sin(θ) + 20 cos(θ))

Multiplying the numerator and denominator by √5, we get:
time = √(5(18000 + 8000 cos(θ))) / √(5(4 + 4 sin(θ) + 4 cos(θ)))

Simplifying once more, we get:
time = 2√(18000 + 8000 cos(θ)) / √(4 + 4 sin(θ) + 4 cos(θ))

Therefore, the expression for the time it takes the man to cross the river at an angle θ to the direction of the current is:
time = 2√(18000 + 8000 cos(θ)) / √(4 + 4 sin(θ) + 4 cos(θ))

15.) The weight X of a particular animal is normally distributed with μ= 200kg and σ= 15kg. An animal of this population is overweight if it has a weight greater than 230 kg

a) Find the probability that an animal is overweight.
P (X>230) = 0.02275

b) We select 2 animals from this population. Find the probabilities that
i) both animals are overweight
(0.02275)2= 0.000518

ii) only one animal is overweight.
0.02275)* (1-0.02275)* 2 = 0.0445

c) We select 7 animals from this population. Find the probability that exactly two of them are overweight.
Y follows B(n,p) with n = 7, p =0.02275
P(Y=2) = 0.00969

16.) An amount of $10,000 is invested at an annual interest rate of 12%.

a) Find the value of the investment after 5 years

i) if the interest rate is compounded yearly;
FV=10000(1+12/100)n
n= 5, 17623.42

ii) if the interest rate is compounded half-yearly;
n= 10, 17908.48

iii) if the interest rate is compounded quarterly;
n=20, 18061.11

iv) if the interest rate is compounded monthly.
n= 5*12, 18166.97

b) The value of the investment will exceed $ 20 000 after n full years. Calculate the minimum value of n

i) if the interest rate is compounded yearly;
20000= 10000(1+12/100)n
n=6.11, hence n=7

ii) if the interest rate is compounded monthly.
20000= 10000(1+12/100)12n
n=5.81, hence n=6

17.) A box contains 4 red balls, 6 blue balls, and 5 green balls. A ball is randomly selected from the box, and not replaced, and then a second ball is randomly selected from the remaining balls in the box.

a) Find the probability that the first ball selected is red and the second ball selected is blue.
P(Red, Blue) = (4/15) * (6/14) = 24/105

b) Find the probability that the first ball selected is red or the second ball selected is blue.
P(Red or Blue) = P(Red) + P(Blue) – P(Red, Blue) = (4/15) + (6/15) – (24/105) = 40/105

c) Find the probability that the first ball selected is red and the second ball selected is green, given that the first ball selected is red.
P(Green|Red) = P(Red, Green) / P(Red) = (5/15) / (4/15) = 5/4

d) Find the probability that the first ball selected is blue, given that the second ball selected is green.
P(Blue|Green) = P(Green, Blue) / P(Green) = (2/14) / (5/15) = 4/25

e) Are the events “the first ball selected is red” and “the second ball selected is green” independent? Justify your answer.
The events “the first ball selected is red” and “the second ball selected is green” are not independent, because P(Green|Red) is not equal to P(Green).

18.) Consider the geometric sequence 10, 5, 2.5, 1.25, …

a) Write down the first term u1 and the common ratio r.
u1= 10, r= 0.5

b) Find the 10th term of the sequence.
0.0195

c) Find the sum of the first 10 terms.
19.98

d) Express the general term un in terms of n.
10*0.5(n-1)

e) Hence find the value of n given that un.03125
n= 6

19.) A spherical balloon is being inflated such that the volume V (in cubic centimetres) of the balloon at time t (in seconds) is given by the equation V(t) = (4/3)πr(t)³, where r(t) is the radius of the balloon at time t.

a) Find an expression for the rate of change of the volume with respect to time, dV/dt.
To find the rate of change of the volume with respect to time, we need to differentiate the volume function V(t) with respect to t.
V(t) = (4/3)πr(t)³
Using the chain rule, we can differentiate V(t) with respect to t:
dV/dt = d/dt[(4/3)πr(t)³]
= (4/3)π * d/dt[r(t)³]
= (4/3)π * 3r(t)² * dr(t)/dt
= 4πr(t)² * dr(t)/dt
So, the expression for the rate of change of the volume with respect to time is dV/dt = 4πr(t)² * dr(t)/dt.

b) Given that the radius is increasing at a constant rate of 2 cm/s, find the rate of change of the volume when the radius is 5 cm.
Given that the radius is increasing at a constant rate of 2 cm/s (dr(t)/dt = 2 cm/s) and the radius is 5 cm (r(t) = 5 cm), we can substitute these values into the expression for dV/dt:
dV/dt = 4πr(t)² * dr(t)/dt
= 4π(5 cm)² * (2 cm/s)
= 4π * 25 cm² * 2 cm/s
= 200π cm³/s
Therefore, when the radius is 5 cm and increasing at a rate of 2 cm/s, the rate of change of the volume is 200π cm³/s.

c) Determine the radius at which the rate of change of the volume is maximum and find the corresponding maximum rate of change of the volume.
To find the radius at which the rate of change of the volume is maximum, we need to find the critical points of dV/dt.
We already have the expression for dV/dt:
dV/dt = 4πr(t)² * dr(t)/dt
To find the critical points, we set dV/dt equal to zero and solve for r(t):
4πr(t)² * dr(t)/dt = 0
Since 4π and dr(t)/dt are both nonzero constants, we can conclude that r(t)² = 0.
Therefore, the radius at which the rate of change of the volume is maximum is r(t) = 0. However, this value is not physically meaningful in the context of a balloon, as a radius of zero implies that the balloon does not exist.
Hence, in this scenario, there is no valid radius at which the rate of change of the volume is maximum.

20.) In the triangle PQR, PR = 5 cm, QR = 4 cm and PQ = 6 cm. Calculate

a) The size of PQR
5² = 4² + 6² – 2(4)(6)(cosQ)
PQR = 55.8°

b)The area of the triangle PQR
½ (4)(6)(sin55.8)= 9.92cm²

21.) Let f(x) = x³ + 2x² – 5. Find the equation of the line which is tangent to the graph of y = f(x) at the point (1, -2).

The equation of the tangent line at a point (a, f(a)) on the graph of y = f(x) is given by
y = f(a) + f'(a)(x-a), where f'(a) is the derivative of f(x) with respect to x evaluated at x = a.

So, to find the equation of the tangent line at (1, -2), we first need to find f'(x). We can do this using the power rule and the sum rule of derivatives:
f'(x) = 3x² + 4x

Now we can substitute a = 1 into f'(a) to get f'(1) = 3(1)² + 4(1) = 7
Therefore, the equation of the tangent line at (1, -2) is:
y = -2 + 7(x – 1)
y = -2 + 7x – 7
y = 7x – 9

22.) Solve the equation tan2x = 3 for -π≤ x ≤ π

tanx = ±√3
For tanx = √3
x=π/3, x= -2π/3

For tanx = -√3
x=-π/3, x= 2π/3