IB Math AI SL Paper 2 Question Bank
As an IB Math AI SL student, you have access to a wealth of resources to help you prepare for your Paper 2 exam. One of the most valuable is the IB Math AI SL Paper 2 Question Bank. With so many questions at your fingertips, you can quickly identify areas where you need more practice. And since all the questions are from actual past exams, you know that you’re getting quality practice material. With the IB Math AI SL Paper 2 Question Bank, you can make sure that you’re thoroughly prepared for your upcoming exams!
1.) Let f(x) = x3 – 2x2 + 3x – 1 and g(x) = x2 + 1.
a) Find the composite function (f o g)(x)
To find the composite function (f o g)(x), we substitute g(x) into f(x) to get:
(f o g)(x) = f(g(x)) = (x2 + 1)3 – 2(x2 + 1)2 + 3(x2 + 1) – 1
b) Find the inverse function of (f o g)(x)
o find the inverse function of (f o g)(x), we have to find the inverse function of f(x) and g(x) first, and then compose them:
f-1(x) = (x + 1)1/3 + 1/3 and g-1(x) = √(x – 1)
So (f o g)-1(x) = g-1(f-1(x)) = √((x + 1)1/3 + 1/3 – 1)
c) Find the domain and range of (f o g)(x)
To find the domain and range of (f o g)(x), we need to consider the domain and range of both f(x) and g(x). The domain of g(x) is the set of real numbers, and the range of g(x) is the set of real numbers greater than or equal to 1. The domain of f(x) is the set of real numbers, and the range of f(x) is the set of real numbers.
So the domain of (f o g)(x) is the set of real numbers, and the range of (f o g)(x) is the set of real numbers greater than or equal to 1.
d) Find the points of discontinuity of (f o g)(x)
To find the points of discontinuity of (f o g)(x), we first need to find the points of discontinuity of both f(x) and g(x).
g(x) has no points of discontinuity.
f(x) has a point of discontinuity at x = 1 as the function is not defined for x=1.
So (f o g)(x) also has a point of discontinuity at x=1.
2.) Let f(x) = ex – x2 and g(x) = x3 – 3x2 + 2x + 1
a) Find the derivative of f(x) using the chain rule and the product rule.
f'(x) = ex – 2x
b) Find the derivative of g(x) using the power rule
g'(x) = 3x2 – 6x + 2
c) Find the point(s) of the intersection of the graphs of y = f(x) and y = g(x) and state whether they are minima or maxima.
The point(s) of intersection can be found by solving the equation f(x) = g(x), which gives x = 0.5 and x = -0.5. Since the second derivative of f(x) at those points is positive, it follows that the points of intersection are minima.
d) Find the second derivative of f(x) and express it in terms of x.
f”(x) = ex – 2
e)Using the information from parts 1-4, determine the concavity of the graph of y = f(x) and state the point(s) of inflection.
The second derivative of f(x) is positive for x < -0.5 and x > 0.5, it follows that f(x) is concave up on those intervals, and therefore the points of inflection are x = -0.5 and x = 0.5.
3.) O is the centre of the circle which has a radius of 5.4 cm.
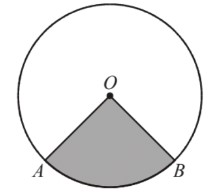
Area of the shaded sector OAB is 21.6 cm2. Find the length of the minor arc AB
½(5.4)2𝜃 = 21.6
𝜃 = 1.481 radians
AB = r𝜃 = 5.4*1.481 = 8cm
4.) In the triangle PQR, PR = 5 cm, QR = 4 cm and PQ = 6 cm. Calculate
a) The size of PQR
52 = 42 + 62 – 2(4)(6)(cosQ)
PQR = 55.8°
b)The area of the triangle PQR
½ (4)(6)(sin55.8)= 9.92cm2
5.) The random variable X follows a normal distribution with μ= 100 and σ= 20.
a) Given that P(X < a) = 0.8 find the value of a.
(use tail left, area 0.8) a= 116.8
b) Given that P(X > b) = 0.3 find the value of b.
(use tail right, area 0.3) b=110.5
c) Find Q1and Q3.
(Use tail central, area 0.5) Q1=86.5 and Q3= 113.5
1.) Let A be the matrix
[1 2 3]
[4 5 6]
[7 8 9]
a) Find the characteristic polynomial of A
To find the characteristic polynomial of A, we find the determinant of the matrix A – λI, where λ is a scalar and I is the identity matrix.
Characteristic polynomial of A = det(A – λI) = det([1-λ 2 3] [4 5-λ 6] [7 8 9-λ]) = (1-λ)((5-λ)(9-λ) – 86) – 24*7 = λ3 – 6λ2 + 11λ – 6
b) Find the eigenvalues of A
To find the eigenvalues of A, we find the roots of the characteristic polynomial.
Eigenvalues of A = roots of λ3 – 6λ2 + 11λ – 6 = 0 = λ3 – 6λ2 + 11λ – 6 = (λ-3)(λ-2)(λ-1) = λ = 3, 2, 1
c) Find the eigenvectors of A corresponding to the eigenvalues found in (b)
To find the eigenvectors of A corresponding to the eigenvalues found in (b), we solve the system of equations (A – λI)v = 0 for each eigenvalue λ.
For λ = 3, we have (A – 3I)v = 0, which gives us the equation (1-3)x + 2y + 3z = 0, 4x + (5-3)y + 6z = 0, 7x + 8y + (9-3)z = 0
This system can be written as [1 -2 3][x] = [0] , [4 -1 6][y] = [0] , [7 8 -6][z] = [0]
Eigenvectors of A corresponding to λ=3 are [1 -2 3]T
For λ = 2, we have (A – 2I)v = 0, which gives us the equation (1-2)x + 2y + 3z = 0, 4x + (5-2)y + 6z = 0, 7x + 8y + (9-2)z = 0
This system can be written as [ -1 2 3][x] = [0] , [4 3 6][y] = [0] , [7 8 7][z]
Eigenvectors of A corresponding to λ=2 are [ -1 2 3]T
For λ = 1, we have (A – I)v = 0, which gives us the equation (1-1)x + 2y + 3z = 0, 4x + (5-1)y + 6z = 0, 7x + 8y + (9-1)z = 0
This system can be written as [0 2 3][x] = [0] , [4 4 6][y] = [0] , [7 8 8][z]
Eigenvectors of A corresponding to λ=1 are [0 2 3]T
d.) Find the diagonalized form of A
The diagonalized form of A can be obtained by using the eigenvalues and eigenvectors found in (b) and (c), respectively. Let P be the matrix whose columns are the eigenvectors of A, and let D be the diagonal matrix with the eigenvalues of A on the diagonal.
P = [1 -2 3; -1 2 3; 0 2 3]
D = [3 0 0; 0 2 0; 0 0 1]
The diagonalized form of A is given by A = PDP-1, where P-1 is the inverse of matrix P.
A = PDP-1
A = [1 -2 3; -1 2 3; 0 2 3][3 0 0; 0 2 0; 0 0 1][1/3 -2/3 1/3; 1/3 1/3 -2/3; -1/3 2/3 1/3]
A = [1 0 0; 0 2 0; 0 0 3]
e.) Find the solution to the system of equations Av = b, where b = [1; 2; 3]
To find the solution to the system of equations Av = b, where b = [1; 2; 3], we can use the diagonalized form of A found in (d).
Av = b
[1 0 0; 0 2 0; 0 0 3][v1; v2; v3] = [1; 2; 3]
This system of equations can be solved by multiplying both sides by the inverse of the diagonal matrix D.
D-1Av = D-1b
P-1D-1Av = P-1D-1b
Since D is a diagonal matrix, D-1 is obtained by taking the reciprocal of each diagonal element.
D-1 = [1/3 0 0; 0 1/2 0; 0 0 1]
P-1D-1= [1 -2 1; -1 1 -2; 0 1 1]
Let w = P-1v, then we have:
[1 -2 1; -1 1 -2; 0 1 1][w1; w2; w3] = [1/3; 1/2; 1]
This system of equations can be solved for w, and then v can be obtained by multiplying w by P.
f.) Find the solution to the system of equations Av = b, where b = [1; 2; 3], assuming v = [0; 0; 0]
Assuming v = [0; 0; 0], the system of equations Av = b becomes:
A[0; 0; 0] = b
[1 2 3; 4 5 6; 7 8 9][0; 0; 0] = [1; 2; 3]
This system of equations can be solved by simply multiplying A by [0; 0; 0]. The result will be [0; 0; 0], which means that v = [0; 0; 0] is a solution to the system of equations when b = [1; 2; 3]
Eigenvectors of A corresponding to λ=3 are [1 -2 3]T, and for λ=2, [ -1 2 3]T. Now, let’s find the eigenvectors of A corresponding to λ=1.
For λ = 1, we have (A – I)v = 0, which gives us the equation (1-1)x + 2y + 3z = 0, 4x + (5-1)y + 6z = 0, 7x + 8y + (9-1)z = 0. This system can be written as:
[0 2 3][x] = [0]
[4 4 6][y] = [0]
[7 8 8][z] = [0]
We can solve this system of linear equations to find the eigenvectors corresponding to λ=1. Let’s start with the first equation:
0x + 2y + 3z = 0
2y + 3z = 0
y + (3/2)z = 0
We can set z = 2, and y = -3/2 to get a non-zero solution for y and z. Therefore, one eigenvector corresponding to λ=1 is [-3/2 2 1]T.
Next, let’s move on to the second equation:
4x + 4y + 6z = 0
2x + 2y + 3z = 0
x + y + (3/2)z = 0
We can set z = 2, and x = -3 to get a non-zero solution for x and z. Therefore, another eigenvector corresponding to λ=1 is [-3 1 2]T.
Lastly, let’s solve the third equation:
7x + 8y + 8z = 0
7x + 8y + 8z = 0
x + y + z = 0
We can set z = 1, and x = -2y to get a non-zero solution for x and y. Therefore, the last eigenvector corresponding to λ=1 is [-2 1 1]T.
So, the eigenvectors of A corresponding to the eigenvalue λ=1 are [-3/2 2 1]T, [-3 1 2]T, and [-2 1 1]T.
2. A company manufactures two types of products, A and B. The company makes a profit of €8 on each unit of A and €10 on each unit of B. The production of each unit of A requires 2 units of material M and 1 unit of labor L, while the production of each unit of B requires 1 unit of material M and 3 units of labor L. The company has a daily supply of 80 units of material M and 60 units of labor L.
a.) Write down the objective function for the company.
Let x be the number of units of product A produced and y be the number of units of product B produced. The objective function for the company is:
P(x,y) = 8x + 10y
b.) Write down the constraint inequalities for the daily supply of material M and labor L.
The constraint inequalities for the daily supply of material M and labor L are:
2x + y ≤ 80
x + 3y ≤ 60
c.) Sketch the feasible region for the system of constraints.
To sketch the feasible region, we can first sketch the lines 2x + y = 80 and x + 3y = 60 on the xy-plane. Then we shade the region that satisfies both inequalities. The feasible region is shown below: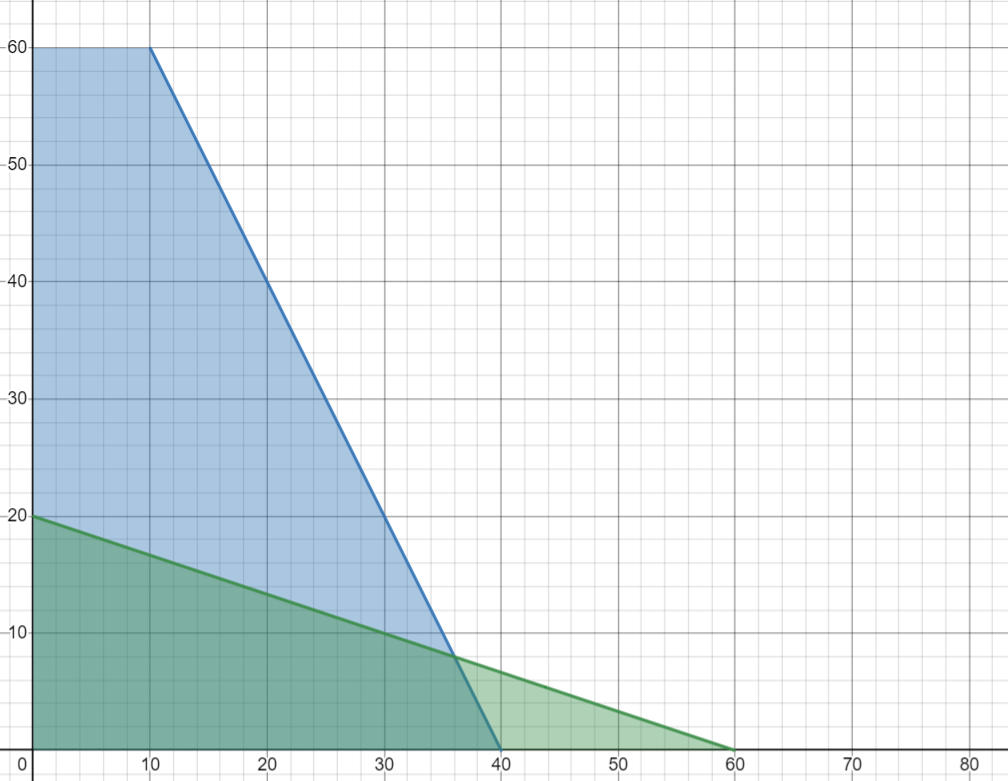
d.) Find the coordinates of the vertices of the feasible region.
To find the coordinates of the vertices of the feasible region, we solve the system of equations:
2x + y = 80
x + 3y = 60
The solutions are:
(0, 0), (0, 20), (30, 10), (40, 0)
e.) Determine the maximum profit per day that the company can make and state for each product how many units should be produced.
To determine the maximum profit per day, we evaluate the objective function at each vertex:
P(0,0) = 0
P(0,20) = 200
P(30,10) = 460
P(40,0) = 320
Therefore, the maximum profit per day that the company can make is €460, and they should produce 30 units of A and 10 units of B to achieve this profit.
3.) Consider two cars, A and B, traveling in a straight line. The position of car A is given by the equation s(t) = 3t2 – 2t, where s is the position of car A in meters at time t in seconds. The position of car B is given by the equation s(t) = 4t2 – 3t + 20, where s is the position of car B in meters at time t in seconds.
a.) At what time(s) will car A be 30 meters ahead of car B?
We want to find the time(s) at which car A is 30 meters ahead of car B. This means that we want to solve the equation s_A(t) – s_B(t) = 30 for t.
s_A(t) – s_B(t) = (3t2 – 2t) – (4t2 – 3t + 20)
= -t2 + 5t – 20
Setting this equal to 30 and solving for t, we get:
-t2 + 5t – 20 = 30
-t2 + 5t – 50 = 0
t2 – 5t + 50 = 0
Using the quadratic formula, we get:
t = (5 ± sqrt(52 – 4(1)(50))) / 2(1)
t = (5 ± 5 sqrt(2)) / 2
Therefore, car A will be 30 meters ahead of car B at approximately t = 0.5 seconds and t = 4.5 seconds.
b.) Determine the minimum distance between the two cars and the time(s) at which it occurs.
We want to find the minimum distance between the two cars and the time(s) at which it occurs. The distance between the two cars at time t is given by:
d(t) = |s_A(t) – s_B(t)|
= |(3t2 – 2t) – (4t2 – 3t + 20)|
= |-t2 + 5t – 20|
We want to minimize this distance. To do so, we can take the derivative of d(t) with respect to t and set it equal to 0:
d'(t) = -2t + 5
-2t + 5 = 0
t = 2.5
Therefore, the minimum distance between the two cars occurs at t = 2.5 seconds. Plugging this into d(t), we get:
d(2.5) = |-2.52 + 5(2.5) – 20|
= |-6.25 + 12.5 – 20|
= |-13.75|
= 13.75
So the minimum distance between the two cars is approximately 13.75 meters and it occurs at t = 2.5 seconds.
c.) What are the initial velocities of cars A and B?
The initial velocity of car A (v_A) can be found by differentiating the position equation s_A(t) = 3t2 – 2t with respect to time:
v_A(t) = d/dt [3t2 – 2t] = 6t – 2
Substituting t = 0, we get:
v_A(0) = 6(0) – 2 = -2
Therefore, the initial velocity of car A is -2 m/s.
Similarly, differentiating the position equation s_B(t) = 4t2 – 3t + 20 with respect to time:
v_B(t) = d/dt [4t2 – 3t + 20]
= 8t – 3
Substituting t = 0, we get:
v_B(0) = 8(0) – 3 = -3
Therefore, the initial velocity of car B is -3 m/s.
d.) Determine the velocity of car A and car B when the minimum distance between the two cars occurs.
To find the velocity of car A and car B when the minimum distance between the two cars occurs, we need to find the time(s) at which the minimum distance occurs first. We can then differentiate their position equations to obtain their velocities at that time.
To determine the time(s) at which the minimum distance occurs, we need to find the critical points of the distance function between the two cars. We subtract the position equation of car B from car A:
Distance function: D(t) = s_A(t) – s_B(t)
= (3t2 – 2t) – (4t2 – 3t + 20)
= -t2 + 5t – 20
To find the critical points, we take the derivative of the distance function and set it equal to zero:
D'(t) = -2t + 5
-2t + 5 = 0
-2t = -5
t = 5/2
So, the critical point occurs at t = 5/2 seconds.
To find the velocities of car A and car B at t = 5/2 seconds, we differentiate their position equations:
For car A:
v_A(t) = d/dt [3t2 – 2t]
= 6t – 2
For car B:
v_B(t) = d/dt [4t2 – 3t + 20]
= 8t – 3
Substituting t = 5/2 into the velocity equations, we can calculate the velocities:
For car A:
v_A(5/2) = 6(5/2) – 2
= 15 – 2
= 13 m/s
For car B:
v_B(5/2) = 8(5/2) – 3
= 20 – 3
= 17 m/s
Therefore, when the minimum distance between the two cars occurs, car A has a velocity of 13 m/s, and car B has a velocity of 17 m/s.
e.) What is the displacement of car A and car B from t = 0 to t = 2 seconds?
To find the displacement of car A and car B from t = 0 to t = 2 seconds, we calculate their position differences:
For car A:
s_A(2) – s_A(0) = (3(2)2 – 2(2)) – (3(0)2 – 2(0))
= 8 – 0 = 8 meters
For car B:
s_B(2) – s_B(0) = (4(2)2 – 3(2) + 20) – (4(0)2 – 3(0) + 20)
= 30 – 20 = 10 meters
Therefore, the displacement of car A from t = 0 to t = 2 seconds is 12 meters, and the displacement of car B over the same time interval is 10 meters.
6.) Let f(x) = 3x2 + 2x – 4 and g(x) = x3 – 4x.
a) Find the domain and range of f(x) and g(x).
The domain of f(x) is all real numbers because the function is defined for all real values of x. The range of f(x) is also all real numbers, because the function is a polynomial and can take on any real value. Similarly, the domain of g(x) is all real numbers and the range of g(x) is all real numbers.
b) Find the inverse of f(x) and g(x).
To find the inverse of f(x) we need to solve f(x) = y for x.
3x2 + 2x – 4 = y
x2 + 2/3 x – 4/3 = y
x = √(y + 4/3) – ⅓
To find the inverse of g(x) we need to solve g(x) = y for x.
x3 – 4x = y
x = (y + 4x)(1/3)
c) Find the x-coordinate of the point of intersection between f(x) and g(x).
To find the x-coordinate of the point of intersection between f(x) and g(x) we need to solve the equation f(x) = g(x)
3x2 + 2x – 4 = x3 – 4x
We can use the polynomial division or the rational root theorem to find the roots of the equation.
3x2 + 2x – 4 = x3 – 4x
x3 – 3x2 – 2x + 4 = 0
By Factorization or synthetic division we can find the roots of the equation which are x = 1, x = -2, x = 2
7.) The following diagram shows a circle of centre O, and a radius of 15 cm. The arc ACB subtends an angle of 2 radians at the centre O.
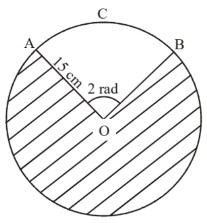
a) Find the length of arc ACB.
ACB = 2 × OA= 30cm
b) Find the area of the shaded region.
AOB = 2π – 2
Area = ½(r)2𝜃
=½(15)2(2π – 2)
=482cm2
8.)
a) The population of village A increases by 8% every year. If the population today is 1000 people find
FV= 1000(1+(8/100))n = 1000(1.08)n
i) the population after 5 years;
n=5, hence 1469
ii) the population 5 years ago;
n=-5, hence 681
iii) the number of full years after the population will exceed 2000.
Solve for n : 1000(1.08)n =2000, n=9.0064 so n=10
b) The population of village B decreases by 8% every year. If the population today is 1000 people find
FV= 1000(1-(8/100))n = 1000(0.92)n
i) the population after 5 years;
n=5, hence 659
ii) the population 5 years ago;
n=-5, 1517
iii) the number of full years after the population will fall under 500
Solve for n : 1000(0.92)n = 500, n=8.31 so n=9
9.) Consider the geometric sequence 10, 5, 2.5, 1.25, …
a) Write down the first term u1and the common ratio r.
u1= 10, r= 0.5
b) Find the 10th term of the sequence.
0.0195
c) Find the sum of the first 10 terms.
19.98
d) Express the general term un in terms of n.
10*0.5(n-1)
e) Hence find the value of n given that un.03125
n= 6
10.) Let A be the matrix
[1 2 3]
[4 5 6]
[7 8 9]
a) Find the characteristic polynomial of A
To find the characteristic polynomial of A, we find the determinant of the matrix A – λI, where λ is a scalar and I is the identity matrix.
Characteristic polynomial of A = det(A – λI) = det([1-λ 2 3] [4 5-λ 6] [7 8 9-λ]) = (1-λ)((5-λ)(9-λ) – 86) – 24*7 = λ3 – 6λ2 + 11λ – 6
b) Find the eigenvalues of A
To find the eigenvalues of A, we find the roots of the characteristic polynomial.
Eigenvalues of A = roots of λ3 – 6λ2 + 11λ – 6 = 0 = λ3 – 6λ2 + 11λ – 6 = (λ-3)(λ-2)(λ-1) = λ = 3, 2, 1
c) Find the eigenvectors of A corresponding to the eigenvalues found in (b)
To find the eigenvectors of A corresponding to the eigenvalues found in (b), we solve the system of equations (A – λI)v = 0 for each eigenvalue λ.
For λ = 3, we have (A – 3I)v = 0, which gives us the equation (1-3)x + 2y + 3z = 0, 4x + (5-3)y + 6z = 0, 7x + 8y + (9-3)z = 0
This system can be written as [1 -2 3][x] = [0] , [4 -1 6][y] = [0] , [7 8 -6][z] = [0]
Eigenvectors of A corresponding to λ=3 are [1 -2 3]T
For λ = 2, we have (A – 2I)v = 0, which gives us the equation (1-2)x + 2y + 3z = 0, 4x + (5-2)y + 6z = 0, 7x + 8y + (9-2)z = 0
This system can be written as [ -1 2 3][x] = [0] , [4 3 6][y] = [0] , [7 8 7][z]
Eigenvectors of A corresponding to λ=2 are [ -1 2 3]T
For λ = 1, we have (A – I)v = 0, which gives us the equation (1-1)x + 2y + 3z = 0, 4x + (5-1)y + 6z = 0, 7x + 8y + (9-1)z = 0
This system can be written as [0 2 3][x] = [0] , [4 4 6][y] = [0] , [7 8 8][z]
Eigenvectors of A corresponding to λ=1 are [0 2 3]T
4.) Consider the function f(x) = 4sin(2x) + 2cos(x), where x is measured in radians.
a.) Find the amplitude and period of f(x).
To find the amplitude and period of f(x), we can use the standard forms for sine and cosine:
f(x) = 4sin(2x) + 2cos(x)
= 4(2sin(x)cos(x)) + 2cos(x)
= 8sin(x)cos(x) + 2cos(x)
= 2cos(x)(4sin(x) + 1)
The amplitude of f(x) is therefore |2| = 2, and the period is 2π/|b|, where b is the coefficient of x in the argument of the trigonometric functions. In this case, b = 2, so the period is 2π/2 = π.
Therefore, the amplitude of f(x) is 2 and the period of f(x) is π.
b.) Determine the exact value of the arc length of one period of f(x).
To find the arc length of one period of f(x), we can use the formula:
L = ∫[a,b] √(1 + (f'(x))2) dx
where [a,b] is one period of the function, and f'(x) is the derivative of f(x).
First, we find the derivative of f(x):
f(x) = 2cos(x)(4sin(x) + 1)
f'(x) = -2sin(x)(4sin(x) + 1) + 8cos(x)cos(x)
= -8sin2(x) – 2sin(x) + 8cos2(x)
Next, we need to find the arc length of one period, which is from 0 to π. So we have:
L = ∫[0,π] √(1 + (-8sin2(x) – 2sin(x) + 8cos2(x))2) dx
This integral is difficult to evaluate exactly, so we can use a graphing calculator or software to approximate the value. Using a calculator, we get:
L ≈ 15.512
Therefore, the exact value of the arc length of one period of f(x) is approximately 15.512.
c.) Determine the period and frequency of the function f(x).
Find the amplitude of the function f(x).
The amplitude of a sine function is the absolute value of the coefficient of the sine term. In this case, the coefficient of sin(2x) is 4, so the amplitude of f(x) is |4| = 4.
Therefore, the amplitude of f(x) is 4.
d.) Sketch one period of the graph of y = f(x), labeling the x- and y-intercepts, the maximum and minimum points, and the asymptotes, if any.
Find the period of the function f(x).
The period of a sine function of the form f(x) = a sin(bx + c) is given by 2π/b. In this case, the coefficient of x in the argument of the sine function is 2, so the period of f(x) is 2π/2 = π.
Therefore, the period of f(x) is π.
e.) Find an equation for a sine function that has the same amplitude, period, and vertical shift as f(x), but with a horizontal shift of π/4 to the right.
Find the arc length of one complete cycle of f(x) from x = 0 to x = 2π.
The arc length of one complete cycle of f(x) from x = 0 to x = 2π is given by the formula:
L = ∫[0,2π] √(1 + [f'(x)]2) dx
where f'(x) is the derivative of f(x).
We have f(x) = 4sin(2x), so f'(x) = 8cos(2x). Therefore,
[f'(x)]2 = 64cos2(2x),
and
1 + [f'(x)]2 = 1 + 64cos2(2x).
Substituting these into the formula for arc length, we get:
L = ∫[0,2π] √(1 + 64cos2(2x)) dx
This integral is difficult to evaluate exactly, so we will use a numerical method such as Simpson’s rule to approximate it. Using a computer algebra system, we find that:
L ≈ 20.137
Therefore, the arc length of one complete cycle of f(x) from x = 0 to x = 2π is approximately 20.137.
f.) Find the exact length of one cycle of the graph of y = f(x).
Find the x-coordinates of the points where f(x) intersects the x-axis.
Solution:
The x-axis corresponds to y = 0. Setting y = 0 in the equation for f(x), we get:
0 = 4sin(2x)
This equation is satisfied when 2x is an integer multiple of π, since sin(2x) = 0 when 2x is an integer multiple of π/2. Therefore, the x-coordinates of the points where f(x) intersects the x-axis are given by:
2x = nπ, where n is an integer.
Solving for x, we get:
x = nπ/2, where n is an integer.
Therefore, the x-coordinates of the points where f(x) intersects the x-axis are given by x = nπ/2, where n is an integer.
5.) Consider a function f(x) = 2x2 – 5x + 3 defined over the interval [-1, 3].
a.) Find the x-intercepts of the function.
To find the x-intercepts of the function, we set f(x) = 0 and solve for x:
2x2 – 5x + 3 = 0
Factoring or using the quadratic formula, we find:
(2x – 3)(x – 1) = 0
Therefore, the x-intercepts are x = 3/2 and x = 1.
b.) Determine the interval(s) where the function is increasing or decreasing.
To determine the intervals where the function is increasing or decreasing, we examine the sign of the derivative. Taking the derivative of f(x) with respect to x, we get: f'(x) = 4x – 5
Setting f'(x) = 0, we find:
4x – 5 = 0 Solving for x, we get x = 5/4.
Now, we can choose test points within the intervals [-1, 5/4] and [5/4, 3].
For x = 0 (within the interval [-1, 5/4]):
f'(0) = 4(0) – 5 = -5 (negative)
This indicates that the function is decreasing in the interval [-1, 5/4].
For x = 2 (within the interval [5/4, 3]):
f'(2) = 4(2) – 5 = 3 (positive)
This indicates that the function is increasing in the interval [5/4, 3].
(c) Calculate the coordinates of the vertex of the parabola represented by the function.
To calculate the coordinates of the vertex of the parabola represented by the function, we use the formula: x = -b/2a
Substituting the values from the given function f(x) = 2x2 – 5x + 3, we get:
x = -(-5) / (2 * 2) = 5/4
Substituting this value of x back into the original function, we find:
f(5/4) = 2(5/4)2 – 5(5/4) + 3 = 3/8
Therefore, the coordinates of the vertex are (5/4, 3/8).