IB Physics HL Paper 3 Question Bank
SECTION A
1.) A wheel of a mass of 0.27 kg that consists of a cylinder is mounted on the central shaft. The radius of the shaft is 1.4 cm and the cylinder, 4.2 cm. The shaft sits on two rails and is allowed to rotate and spin freely.
a.) The wheel is released from a stationary position and it rolls down the rail without slipping from Point A to Point B. The picture below shows the setup
The wheel leaves the rails at Point B and travels along a flat track from Point B to Point C. For a short while, a frictional force F exists towards point C between the edge of the wheel and the flat track
i.) The moment of Inertia of the wheel is 1.5 x 10-4 kgm2. Define inertia
Answer
Inertia is a property of matter that causes it to resist changes in velocity. It remains at the state of rest or in uniform motion in the same straight line unless acted upon by some external force.
ii.) While the wheel moves from Point A to B, the center of mass falls through a vertical distance of 0.43 m. Determine the translational speed of the wheel from Point A to Point after its displacement.
Answer
Kinetic Energy + Rotational KE = Gravitational Potential Energy
Therefore, ½ mv2 + ½ I x v2/r2 = mgh where r is the radius of the shaft
½ x 0.27 x v2 + ½ x 1.5 x 10-4 x v2/ (1.96 x 10-4) = 0.27 x 9.81 x 0.43
Rearranging and finding v, we have v = 1.48 m/s
iii.) Determine the angular velocity of the wheel at Point B
Answer
Angular velocity = velocity / radius (in meters)
Therefore, Angular velocity = 1.48 / 0.014 = 105.7 → 106 rad/s
iv.) Describe the effect of the frictional force on the linear speed of the wheel
Answer
Since the force is in the direction of the motion, the linear speed of the wheel increases.
v.) Describe the effect of the frictional force on the angular speed of the wheel
Answer
The angular speed decreases since the force gives rise to an opposing torque on the wheel.
2.) In an experiment, a student rolls paper into cylinders with the same diameter but different heights. The student then placed a fixed load on top of each of the cylinders one by one beginning with the cylinder with the shortest height. After, they recorded the height H of the first cylinder that was about to collapse. They then repeated the same process with different diameters of the cylinder. The graph below shows all the data recorded by the student. It is predicted that H (height) = cD2/3 where c is the constant
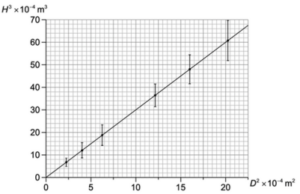
a.) Explain why the students data supports the theoretical prediction
Answer
According to the theoretical prediction, H3 is proportional to D2. When drawn in the graph, it is a straight line that goes through the origin – which is seen in the students graph above. Hence, it suggests that the data matches the prediction.
b.) Determine the constant c with an appropriate unit
Answer
c = gradient of the line
c = (46 – 12) / (16 – 4) = 34/12 = 2.83
c3 = 2.83 → c = 1.41
The unit for c is m1/3
c.) State one factor that would determine the constant c
Answer
The constant c could vary due to a number of factors. Some of them include the thickness of the paper, the weight of the fixed load and the number of times the paper is rolled into a cylinder (thickness of the cylinder itself).
3.) An experiment to determine how the frequency f of a vibrating wire varies with its tension T in the wire.
a.) The data is shown in the graph below with the error bars for frequency
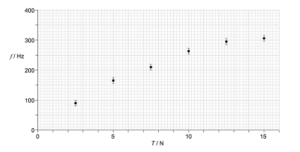
Draw the line of best fit for the data shown above
Answer
The line should be drawn in a way where it passes through all the error bars
b.) It is proposed that the frequency of the oscillation is given by f2 = kT where k is the constant.
i.) Determine the SI unit for constant k
Answer
1 / kg m
ii.) Write down a set of quantities that can be plotted to support the theoretical proposition: f2 = kT
Answer
f2 and T or f and T1/2
iii.) Describe how the characteristics of the graph if it were to support the relationship from b. ii.
Answer
The graph would be a straight line passing through the origin
Don't forget to check our Forum
SECTION B – Option D Astrophysics
1.) Orion is a constellation. A distinctive feature of the constellation is a cluster of stars in the shape of a trapezium.
a.) Differentiate between an open cluster of stars and a constellation
Answer
An open cluster is a type of star cluster made of up to a few thousand stars that were formed from the same giant molecular cloud and are roughly the same age. They are loosely gravitationally bound to each other. Whereas, a constellation is A pattern of stars visible from Earth that are not gravitational bound. However, they (a group of these stars) present themselves as a specific pattern.
b.) The Great Nebula is situated within the Orion constellation. In order for the nebula to form a star, it needs to satisfy the Jeans criterion. Describe the criterion.
Answer
Stars form when a portion of interstellar cloud collapses gravitationally. The Jeans mass criterion is determined by asking when the magnitude of the gravitational potential energy exceeds the magnitude of the gas’s kinetic energy. The collapse of an interstellar cloud may begin if M>Mj where Mj is the Jeans criterion. It can be calculated using a formula.
c.) Betelgeuse is one of the stars present in Orion.
i.) The parallax angle of the Betelgeuse star from Earth is 7.63 x 10-3 arc sec. Calculate the approximate distance from this star to the Earth in parsec.
Answer
The distance in parsec can be found by dividing 1 by the parallax angle
So, 1/7.63 x 10-3 = 131.06 → 131 pc
ii.) Explain why there is only upto a certain distance that astronomers can measure using stellar parallax
Answer
Parallax angles of less than 0.01 arcsec are very difficult to measure from Earth because of the effects of the Earth’s atmosphere. This limits Earth based telescopes to measuring the distances to stars about 1/0.01 or 100 parsecs away.
2.) This question is related to Cepheid variables
a.) Define Cepheid variables
Answer
Cepheids, also called Cepheid Variables, are stars which brighten and dim periodically. Cepheid variables periods (i.e., the time for one cycle) of variation are closely related to their luminosity and that are therefore useful in measuring interstellar and intergalactic distances.
b.) Explain how Cepheid variables are used to determine distances
Answer
The Cepheid variable’s apparent brightness is compared with its intrinsic brightness. The difference between observed and actual brightness yields the distance. The actual brightness or the peak luminosity depends on the period of the cepheid variable. More luminous Cepheid variables have greater periods therefore measurements of apparent brightness allow distance determination.
c.) Outline the processes that cause a change in luminosity of the cepheid variables
Answer
Cepheid stars generally expand and contract. So, simultaneously when this happens, their surface area increases and decreases, their surface temperature decreases then increases and they become transparent and opaque. The cepheid variable is opaque when it is at its dimmest.
d.) The following data are about a cepheid variable
Peak luminosity: 7.6 x 1029W
Peak wavelength of light: 4.25 x 10-7 m
Distance from the Earth: 271 pc
i.) Calculate the peak apparent brightness of this cepheid variable as observed from the Earth
Answer
To find the apparent brightness, this formula can be used: b = L / 4πd2
To use this, we need to find d in terms of m. We have value in parsecs – 271 pc
Therefore, to convert it, the value of parsec will be multiplied with 3.26 because 3.26 light years make up one parsec. And to convert light years to meters, we multiply that with 9.46 x 1015.
Hence, we have → 271 x 3.26 x 9.46 x 1015 = 8.357 x 1018 m
Substituting this distance in the initial formula along with the other data, we have:
B = 7.6 x 1029 / 4π x (8.357 x 1018)2 → B = 8.66 x 10-10 W/m2
ii.) Calculate the peak surface temperature of the cepheid
Answer
To calculate the peak surface temperature, the formula T = b/λmax can be used where b is the Wien’s Displacement constant → T = 2.897 x 10-3 / 4.25 x 10-7 = 6816.4 K which can approximately be rounded to 6800 K.
3.) A supernova is a star that suddenly increases greatly in brightness because of a catastrophic explosion that ejects most of its mass. It is essentially an explosion of a supergiant star
a.) Outline how
i.) a type 1a supernova is formed
Answer
Type 1a supernova is a type of supernova that occurs in binary systems (i.e. two stars orbiting one another) in which one of the stars is a white dwarf. When the white dwarf star mass reaches the Chandrasekhar limit, the star explodes due to fusion reactions.
ii.) type 1a supernovae could be used to measure the distance to a galaxy
Answer
So when astronomers observe a type Ia supernova, they can measure its apparent magnitude, knowing what its absolute magnitude is. They can then use the distance modulus to calculate the distance to the supernova, and the galaxy that it is in.
b.) Outline how a type 2 supernova is formed
Answer
A Type II supernova results from the rapid collapse and violent explosion of a massive star. It is associated with the core collapse of a massive star together with a shock-driven expansion of a luminous shell which leaves behind a rapidly rotating neutron star or, if the core has mass of >2–3 solar masses, a black hole. The star must have at least 8 times, but no more than 40 – 50 times, the mass of the Sun (M☉) to undergo this type of explosion.
c.) Outline why a neutron star that is left after the supernova stage does not collapse under the action of gravitation.
Answer
Gravitation is balanced by a pressure/force due to neutrons hence doesn’t collapse
4.) The Hertzsprung-Russell diagram is shown below. It shows several types of stars with different luminosity.
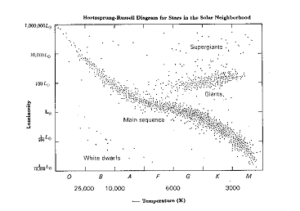
a.) The Sun has a luminosity of L0 . Mark the position of the Sun on the diagram above
Answer
Point marked in the main sequence. The data point is 1 L luminosity and a little more than 5000 K as its effective temperature.
b.) The Sun can become a red giant. Outline under what conditions it can become one
Answer
As soon as the sun begins to burn more hydrogen, it would be considered a “red giant”. The process of compression in the center allows the outer regions of the star to expand outwards. The burning hydrogen in the shell around the core significantly increases the brightness of the sun. A red giant forms after a star has run out of hydrogen fuel for nuclear fusion, and has begun the process of dying.
c.) Outline why the Sun will have a constant radius after it becomes a white dwarf
Answer
It is because of electron degeneracy. Electron degeneracy pressure will halt the gravitational collapse of a star if its mass is below the Chandrasekhar limit (1.44 solar masses) which it is since we’re talking about the Sun here. This is the pressure that prevents a white dwarf star from collapsing.
5.) This question is related to dark matter and cosmic background radiation.
a.) Describe what dark matter is
Answer
Dark matter is matter in galaxies that are too cold to radiate. Dark matter is composed of particles that do not absorb, reflect, or emit light, so they cannot be detected by observing electromagnetic radiation.
b.) State two candidates for dark matter
Answer
Blackholes and Neutrinos
c.) Define Cosmic Microwave Background Radiation
Answer
CMB is the cooled remnant of the first light that could ever travel freely throughout the Universe. It is the ‘left over’ radiation from the big bang during the initial hot explosion. It is an electromagnetic radiation that has very low frequency and is emitted from all parts of the universe, in all directions.
https://www.iitianacademy.com/ib-dp-physics-topic-2-mechanics-question-bank-sl-paper-3/
https://www.iitianacademy.com/ib-dp-physics-topic-2-mechanics-question-bank-sl-paper-3/
Get access to our free IB resources
IBDP Study Notes
IB Comprehensive Syllabus
IB IA Ideas
IB CAS Ideas
