IB Physics SL Paper 3 Question Bank
The IB Physics SL Paper 3 Question Bank is an incredible resource for students preparing for the IB Physics SL Paper 3 examination. In addition to the practice questions, the Question Bank also includes detailed answer explanations that will help students better understand the concepts they are being tested on. The IB Physics SL Paper 3 Question Bank is an essential tool for any student serious about doing well on the IB Physics SL Paper 3 examination.
Time: 1 hour
Instructions to candidates
- Answers must be written within the answer boxes provided.
- A calculator is required for this paper.
- A clean copy of the physics data booklet is required for this paper.
- The maximum mark for this examination paper is [35 marks].
SECTION A
1.) The circuit below can be used to measure the internal resistance of a cell
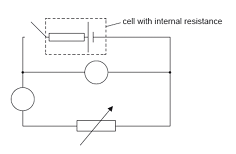
a.) Label the ammeter as A and the voltmeter as V in the circuit
Answer
The circle connected in series is the Ammeter and the circle connected in the parallel circuit is the Voltmeter. A voltmeter is placed in parallel with the voltage source to receive full voltage and must have a large resistance to limit its effect on the circuit. An ammeter is placed in series to get the full current flowing through a branch and must have a small resistance to limit its effect on the circuit.
b.) Upon performing an experiment, the graph for the current vs potential difference is shown below. Using the graph, calculate the best or closest estimate for the resistance of the cell.
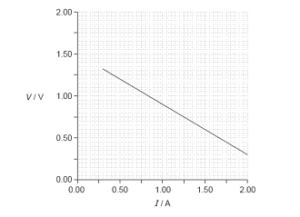
Answer
To find the resistance of the cell, the gradient of the slope needs to be calculated. Therefore, to calculate the gradient of the line, two points that form a large triangle need to be taken. Therefore, for instance, 2 points on the line – (0.40, 1.25) and (2.00, 0.3) – were taken. To find the gradient of the slope, m = y2 – y1 / x2– x1 = (0.3 – 1.25) / (2.00 – 0.30) = 0.95 / 1.7 = 0.558 approximately, 0.56 A.
c.) The student forgets to take a zero error reading from the ammeter. Define zero error reading
Answer
When a circuit is not connected, the ammeter or voltmeter’s pointer is supposed to be at zero, Therefore, a zero error reading is when a non zero reading is displayed when it is supposed to show zero. It is essentially a calibration error.
d.) After the student has taken the zero error reading, she notices it to be a positive number. Explain the effect of a positive zero error reading on the internal resistance of the cell.
Answer
A positive number on the ammeter means that more electricity is being received by the battery than is being used, suggesting the regulator is not working efficiently. All the measurements would be higher and incorrect. Nevertheless, since the value of all of it increases, there will be no change in the internal resistance (the slope of the graph).
2.) This question is about a standing wave in a vibrating string
a.) Describe how a standing wave is formed when the string is fixed at both ends
Answer
The wave travels down the string, hits the end and reflects back. Therefore, the incident wave approaching the end and the reflected wave is interfered or superposed to create a standing wave.
b.) The string of a guitar vibrates at 350 Hz. The length of this guitar string is 0.69 m. Using this data, calculate the velocity of the wave in the string.
Answer
First the wavelength is calculated; λ = 2L → 2 x 0.69 = 1.38 m
Then, the velocity is calculated by multiplying it with the frequency:
v = λf → 1.38 x 350 = 483 m/s
3.) A student pours a can of a carbonated drink into a cylindrical cup after rigorously shaking the can. A large volume of foam is produced eventually filling the container. The graph below shows the time vs the height of the foam:
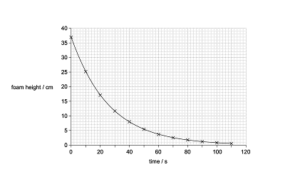
a.) Determine the time taken for the foam to drop to half of its original height
Answer
The initial height of the foam (0 seconds) was 37 cm. Therefore, half of its height will be 18.5 cm. To find the time taken, the data point of time when the height is 18.5 cm will be the answer. By checking the graph, the time taken is between 18 to 19 seconds.
b.) Determine the time taken for the foam to drop to quarter of its original height
Answer
Quarter of the foam height = ¾ x 37 = 27.75 cm
Since the height is reduced, it needs to be subtracted from 37 → 37 – 27.75 = 9.25 cm
Checking the data point, the time taken is 36 to 37 seconds.
SECTION – B
OPTION A – Relativity
This option explores Albert Einstein’s theories of Special and General Relativity. Special Relativity deals with the behavior of objects moving at constant speeds, particularly when they approach the speed of light. It introduces concepts like time dilation and length contraction. General Relativity, on the other hand, focuses on the gravitational effects of massive objects and introduces the idea of curved spacetime. Students will learn about the fascinating and counterintuitive effects of relativity, such as time dilation and the bending of light around massive objects like black holes.
1.)
a.)
i.) Explain the principle of equivalence in general relativity
Answer
The principle of equivalence in general relativity states that there is no experiment that can distinguish between a uniform gravitational field and a uniform acceleration. This means that an observer in a closed laboratory cannot determine whether the laboratory is at rest in a gravitational field or accelerating uniformly in the absence of gravity.
ii.) Calculate the gravitational force between two objects with masses of 5 kg and 10 kg that are separated by a distance of 2 meters.
Answer
The gravitational force between two objects is given by the formula F = Gm1m2/r^2, where G is the gravitational constant (6.67 x 10-11 Nm2/kg2), m1 and m2 are the masses of the two objects, and r is the distance between them. Plugging in the values, we get F = (6.67 x 10-11) x (5) x (10) / (22) = 4.16875 x 10-10 N.
c.)
i.) State the postulates of special relativity.
Answer
The postulates of special relativity are:
1. The laws of physics are the same for all observers in uniform motion relative to one another.
2. The speed of light in a vacuum is the same for all observers, regardless of their relative motion.
2.)
a.)
i.) Explain the concept of time dilation in special relativity.
Answer:
Time dilation in special relativity is the phenomenon that the time interval between two events is measured differently by observers in relative motion. Specifically, an observer in motion relative to an event will measure a longer time interval between the events than an observer at rest with respect to the events.
(ii.) Calculate the time dilation factor for a clock moving at a speed of 0.9c.
The time dilation factor γ is given by γ = 1 / √(1 – v2/c2), where v is the velocity of the moving clock and c is the speed of light. Plugging in the values, we get γ = 2.29.
b.) State the principle of conservation of energy and explain how it is modified in general relativity.
Answer:
The principle of conservation of energy states that the total energy in a closed system is constant. In general relativity, this principle is modified by the presence of gravitational fields, which cause space and time to be curved. The curvature of space and time affects the motion of particles and the flow of energy, such that the conservation of energy takes on a more complex form.
3.)
a.)
i.) Explain the concept of length contraction in special relativity
Answer:
Length contraction in special relativity is the phenomenon that the length of an object appears shorter when it is in motion relative to an observer. Specifically, an observer in motion relative to an object will measure a shorter length of the object than an observer at rest with respect to the object.
ii.) Calculate the length of a spaceship that is moving at 0.8c relative to an observer, given that the spaceship is measured to be 60 meters long in its rest frame.
Answer:
The length of the spaceship as measured by the observer is given by L = L0 / γ, where L0 is the length of the spaceship in its rest frame and γ is the time dilation factor. Plugging in the values, we get L = 25.98 meters.
b)
i.) Explain the concept of time-like and space-like events in special relativity
Answer:
In special relativity, an event is defined by a specific location and time in spacetime. A time-like event is one where the time coordinate is the most significant, meaning that it lies inside the light cone of another event. A space-like event is one where the spatial distance is the most significant, meaning that it lies outside the light cone of another event.
ii.) Calculate the proper time interval between two events that are separated by a distance of 1 light-year in the rest frame of an observer, given that the observer measures the time interval to be 2 years.
Answer:
The proper time interval between two events is given by Δτ = Δt / γ, where Δt is the time interval measured by the observer and γ is the time dilation factor. The distance between the events in the rest frame of the observer is 1 light-year, which is equivalent to 9.46 x 1015 meters. The time dilation factor is given by γ = 1 / √(1 – v2/c2), where v is the velocity of the observer and c is the speed of light. Assuming the observer is at rest, we have γ = 1. Plugging in the values, we get Δτ = 2 / 1 = 2 years.
4.)
a.) Discuss the limitations of the Galilean transformation equations in the context of electromagnetic phenomena.
Answer:
The Galilean transformation equations are valid only for low velocities compared to the speed of light, because they do not take into account the fact that the speed of light is the same in all reference frames. This leads to contradictions when applied to electromagnetic phenomena, such as the fact that the speed of light should be different for observers moving in opposite directions.
b.)
i.) Derive the Lorentz transformation equations for velocity from the point of view of an observer moving at a constant velocity relative to a stationary observer.
Answer:
The Lorentz transformation equations for velocity are:
● x = γ(x’ + vt’)
● y = y’
● z = z’
● t = γ(t’ + vx’/c2)
where γ = 1/√(1 – v2/c2) is the Lorentz factor, x, y, z, t are the coordinates of an event in the stationary observer’s reference frame, and x’, y’, z’, t’ are the coordinates of the same event in the moving observer’s reference frame. The x-axis is parallel to the relative velocity v between the two frames.
OPTION B – Engineering Physics
This option is designed to provide students with insights into the practical applications of physics in the field of engineering. It covers topics such as materials science, fluid dynamics, and thermodynamics, which are essential for understanding the principles behind various engineering technologies. Students will learn how physics concepts are applied in the design and operation of engineering systems, making it a valuable option for those interested in pursuing engineering or related fields in the future.
1.)
a.)
i.) Define stress and strain.
Answer:
Stress is defined as the force per unit area that acts on a material. Strain is the measure of the deformation or elongation of a material due to the applied stress.
ii.) A copper wire with a diameter of 2 mm and length of 1 m is stretched with a force of 500 N. Determine the stress and strain experienced by the wire.
Answer:
Stress = Force/Area = (500 N)/(π*(2 mm/2)2) = 99.6 MPa. Strain = Change in length/Original length = Force*(Length/Area)/Young’s modulus = (500 N)(1 m)/(π(1 mm)2*120 GPa) = 1.30 x 10-3.
b.) A student is designing a bridge to span a river. Discuss the different types of bridges that can be used and their advantages and disadvantages.
Answer:
Different types of bridges include beam bridges, arch bridges, suspension bridges, and cable-stayed bridges. Beam bridges are the simplest type and are good for short spans, but not ideal for long distances. Arch bridges are strong and can span longer distances, but require a stable base. Suspension bridges can span long distances and are strong, but require large anchorages and towers. Cable-stayed bridges are similar to suspension bridges, but require fewer towers and can be more cost-effective.
2.)
a.)
i.) A thin rod of length L and mass M is free to rotate about its end perpendicular to its length. Calculate the moment of inertia of the rod.
Answer:
When a thin rod of length L and mass M is free to rotate about its end perpendicular to its length, its moment of inertia can be calculated as I = (1/3)ML2.
ii.) A solid sphere of mass M and radius R rolls without slipping down an inclined plane. Determine the velocity of the center of mass of the sphere when it reaches the bottom of the plane, assuming no energy is lost to friction.
Answer:
When a solid sphere of mass M and radius R rolls without slipping down an inclined plane, its velocity can be calculated using conservation of energy. The potential energy at the top of the plane is converted to kinetic energy at the bottom, so Mgh = (1/2)Mv2 + (1/2)Iω2, where h is the height of the plane, v is the velocity of the center of mass, and ω is the angular velocity of the sphere. Since the sphere is rolling without slipping, v = Rω, so the equation becomes Mgh = (1/2)Mv2 + (1/2)(2/5)MR2(v/R)2. Solving for v, we get v = √(10gh/7).
b.)
i.) A uniform rod of length L and mass M is pivoted at one end and swings in a vertical plane. Determine the maximum height the rod reaches.
Answer:
When a uniform rod of length L and mass M is pivoted at one end and swings in a vertical plane, the maximum height it reaches can be calculated using conservation of energy. At the highest point of its motion, all of its energy is potential energy, so (1/2)Mv2 = Mgh, where v is the velocity of the rod and h is the maximum height it reaches. Since the rod is pivoted at one end, its moment of inertia is I = (1/3)ML2 about the pivot point, so v = √(2gh/3).
3.)
a.)
i.) State the first law of thermodynamics.
Answer:
The first law of thermodynamics, also known as the law of conservation of energy, states that the total energy of an isolated system is constant; energy can be transformed from one form to another, but it cannot be created or destroyed.
b.)
i.) A gas is compressed adiabatically from an initial volume of V1 to a final volume of V2. Determine the work done by the gas during the process.
Answer:
If a gas is compressed adiabatically, then Q = 0 and the first law of thermodynamics reduces to dU = -dW, where dU is the change in internal energy and dW is the work done by the gas. For an adiabatic process, PVγ = constant, where γ is the ratio of specific heats. Therefore, the work done by the gas during the process can be calculated as follows:
W = ∫PdV = ∫(PVγ)/V dV = (PVγ)/(γ-1) [from V1 to V2]
W = (P1V1γ – P2V2γ)/(γ-1)
Answer:
The maximum efficiency of a heat engine operating between two reservoirs at temperatures T1 and T2 is given by ηmax = 1 – (T2/T1).
OPTION C – Imaging
This option focuses on the physics behind various imaging techniques used in science and medicine. Students will explore the principles of optics, wave phenomena, and the behavior of electromagnetic radiation. Topics may include X-ray imaging, MRI (Magnetic Resonance Imaging), microscopy, and more. This option is particularly relevant for students interested in medical imaging, diagnostic technology, or careers in the field of healthcare.
1.)
a.)
i.) Define attenuation and dispersion in the context of optical fibers.
Answer
Attenuation refers to the decrease in signal strength as it propagates through an optical fiber due to various factors such as absorption, scattering, and bending losses. Dispersion, on the other hand, refers to the broadening of the pulse as it travels through the fiber, caused by different wavelengths of light traveling at different speeds due to the refractive index of the fiber.
ii.) Explain how attenuation and dispersion can limit the performance of a fiber optic communication system.
Answer
Attenuation and dispersion can limit the performance of a fiber optic communication system by reducing the quality of the transmitted signal. Attenuation can result in a loss of signal strength, making it difficult to detect the transmitted signal at the receiver end. Dispersion can cause the signal to spread out in time and frequency, leading to distortion and errors in the received data.
b.)
i.) Explain how chromatic and modal dispersion can occur in a fiber optic cable.
Answer
Chromatic dispersion occurs due to the fact that different wavelengths of light travel at different speeds in the fiber, causing the signal to spread out over time. Modal dispersion, on the other hand, occurs when different modes of light, each with a slightly different propagation time, interfere with each other, causing the signal to spread out over distance.
ii.) Describe two techniques that can be used to reduce the effects of dispersion in fiber optic communication systems.
Answer
Two techniques that can be used to reduce the effects of dispersion in fiber optic communication systems are dispersion-shifted fibers and dispersion-compensating fibers. Dispersion-shifted fibers are designed to have a zero-dispersion wavelength, where the chromatic dispersion is minimized. Dispersion-compensating fibers are used to introduce a compensating dispersion that cancels out the dispersion caused by the transmission fiber.
2.)
a.)
i.) Explain how an astronomical refracting telescope produces an image.
Answer
An astronomical refracting telescope uses a convex lens, called the objective lens, to gather and focus light from a distant object. The light then passes through the lens and forms an inverted, real image at the focal point. A second lens, called the eyepiece, is used to magnify the image and make it visible to the observer.
ii.) Describe one advantage and one disadvantage of using a refracting telescope for astronomical observations.
Answer
One advantage of using a refracting telescope for astronomical observations is that they offer excellent image quality and sharpness. One disadvantage is that they can suffer from chromatic aberration, which is caused by different wavelengths of light refracting differently through the lens and causing the image to appear blurred and discolored.
b.) A fibre optic cable has a core diameter of 50 micrometres and a cladding diameter of 125 micrometres. Calculate the numerical aperture of the cable.
Answer
The numerical aperture of the fiber optic cable can be calculated using the formula:
Numerical aperture = √(n12 – n22)
Where n1 is the refractive index of the core and n2 is the refractive index of the cladding. Assuming the refractive indices are 1.5 and 1.45 for the core and cladding, respectively, the numerical aperture can be calculated as:
Numerical aperture = √(1.52 – 1.452) = 0.39
Therefore, the numerical aperture of the cable is 0.39.
c.)
i.) Explain how a fibre optic bundle can be used for imaging.
Answer
A fiber optic bundle is a collection of small diameter fibers that are arranged in a bundle to transmit images. Light entering the input end of the bundle is transmitted through the individual fibers and emerges as a corresponding pattern at the output end of the bundle, forming a complete image.
ii.) Describe the difference between coherent and incoherent fibre optic bundles.
Answer
Coherent fiber optic bundles transmit light in a way that preserves the phase relationship between individual fibers, resulting in a more accurate image. Incoherent fiber optic bundles do not preserve the phase relationship, resulting in a less accurate image.
iii.) State one application of each type of fibre optic bundle.
Answer
An application of a coherent fiber optic bundle is in medical endoscopy, where the precise imaging capabilities are important. An application of an incoherent fiber optic bundle is in decorative lighting, where the image quality is less critical.
Option D Astrophysics
3.) The surface temperature of the star Epsilon Indi is 4650 K
a. Determine the peak wavelength of the emitted radiation by Epsilon Indi
Answer
The formula λ = b/T is used where b is the Wien’s displacement constant – 2.89 x 10-3
Therefore, substituting the temperature as well, we have: λ = 2.89 x 10-3/4650
λ = 621.5 nm = 622 nm
b. The data shown below is about the Sun
Surface temperature – 5780 K
Luminosity – L0
Radius – R0
Mass – M0
Epsilon Indi has a radius of 0.731 R0.) Determine the luminosity of the star
Answer
L/L0 = (0.731 R0 / R0)2 x (4650 / 5780)4
L/L0 = 0.53436 x 0.41889
L = 0.22383L0 → 0.224 L0
c. Epsilon Indi is a star in the main sequence. Determine the mass of the star
Answer
The relationship between luminosity and mass is L = M3.5
Therefore, M = L1/3.5 M0
Substituting the luminosity we have, M = 0.2241/3.5 M0
M = 0.652 M0
d. Outline the stages the star, Epsilon Indi undergoes once it leaves main sequence till its final stable state
Answer
A star stays in the main sequence until all of the hydrogen has fused to form helium. The helium core now starts to contract further and reactions begin to occur in a shell around the core. Once the core is hot enough for the helium to fuse to form carbon, the outer layers begin to expand, cool and shine less brightly. The expanding star is now called a Red Giant. The helium core runs out, and the outer layers drift away from the core as a gaseous shell, this gas that surrounds the core is called a Planetary Nebula. The remaining core is now in its final stages. When the core becomes a White Dwarf the star eventually cools and dims. When it stops shining, it becomes a dead star and is called a Black Dwarf.
4.) Shown below is a Hertzsprung-Russell Diagram. The following data is available for a star X with respect to the Solar mass (M0) and the Solar Radius (R0):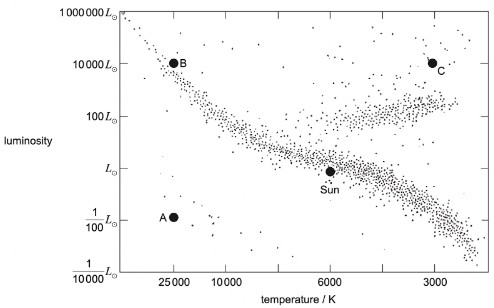
Mx = 4.7 M0
Rx = 3.4 R0
e.) By how much is the luminosity of the star X greater than the luminosity of the sun
Answer
Lx = 4.73.5 M0 since the relationship between luminosity and mass is L = M3.5
Therefore, 4.73.5 = 225 L0
f.) The parallax angle of star X from Earth is 0.174 arc second. Outline how the parallax angle of a star can be measured
Answer
The position of a star is recorded in a 6 month gap (Month 1 and Month 7). The parallax angle is calculated by seeing how much the star has moved relative to the distant stars present in the background.
g.) Star X eventually becomes a White Dwarf.
i.) State the star type for A, B and C
Answer
A: White Dwarfs
B: Main sequence
C: Red Giant
ii.) State what prevents Star X from collapsing further after becoming a white dwarf
Answer
An electron degeneracy. Electron degeneracy pressure will halt the gravitational collapse of a star if its mass is below the Chandrasekhar limit (1.44 solar masses) which it is since we’re talking about the Sun here. This is the pressure that prevents a white dwarf star from collapsing.
5.) Light from a galaxy far away observed on Earth shows a redshift of 0.13.
h.) Define redshift
Answer
Redshift is when the wavelength of the light is stretched, so the light is seen as ‘shifted’ towards the red part of the spectrum. It means that the received wavelength is longer than the emitted wavelength.
i.) Determine the distance to this galaxy using the Hubble constant assuming that it is H0 = 67 km/s Mpc
Answer
First the velocity needs to be determined using the formula v = zc where z is the redshift and c is the speed of light. Therefore, substituting the respective values, we have: v = 0.13 x 3.0 x 105 = 3.9 x 104 km/s. To find the distance, the formula d = v / H0 can be used. Putting in the values, we have, d = 3.9 x 104 / 67 = 582 Mpc
j.) Suggest how the cosmic microwave background radiation provides strong evidence for the existence of the Big Bang model.
Answer
According to the Big Bang theory, the early universe was an extremely hot place, and as it expanded, the gas inside of it cooled. Therefore, radiation known as the “cosmic microwave background,” or CMB, which is essentially the leftover heat from the Big Bang, should be present everywhere in the cosmos. The CMB radiation is essentially a black body spectrum that is highly isotropic across the universe. The wavelength of this CMB radiation matched the predicted wavelength of the Big Bang had it increased by expansion.
OPTION D – Astrophysics
Astrophysics is the study of the universe beyond our planet. This option delves into the physics of celestial objects, galaxies, and the cosmos as a whole. Students will learn about topics like the life cycle of stars, the behavior of galaxies, cosmology, and the Big Bang theory. This option is perfect for those who have a passion for space exploration and a desire to understand the fundamental laws governing the universe.
1.) The surface temperature of the star Epsilon Indi is 4650 K
a.) Determine the peak wavelength of the emitted radiation by Epsilon Indi
Answer
The formula λ = b/T is used where b is the Wien’s displacement constant – 2.89 x 10-3
Therefore, substituting the temperature as well, we have: λ = 2.89 x 10-3/4650
λ = 621.5 nm = 622 nm
b.) The data shown below is about the Sun
Surface temperature – 5780 K
Luminosity – L0
Radius – R0
Mass – M0
Epsilon Indi has a radius of 0.731 R0. Determine the luminosity of the star
Answer
L/L0 = (0.731 R0 / R0)2 x (4650 / 5780)4
L/L0 = 0.53436 x 0.41889
L = 0.22383L0 → 0.224 L0
c.) Epsilon Indi is a star in the main sequence. Determine the mass of the star
Answer
The relationship between luminosity and mass is L = M3.5
Therefore, M = L1/3.5 M0
Substituting the luminosity we have, M = 0.2241/3.5 M0
M = 0.652 M0
d.) Outline the stages the star, Epsilon Indi undergoes once it leaves main sequence till its final stable state
Answer
A star stays in the main sequence until all of the hydrogen has fused to form helium. The helium core now starts to contract further and reactions begin to occur in a shell around the core. Once the core is hot enough for the helium to fuse to form carbon, the outer layers begin to expand, cool and shine less brightly. The expanding star is now called a Red Giant. The helium core runs out, and the outer layers drift away from the core as a gaseous shell, this gas that surrounds the core is called a Planetary Nebula. The remaining core is now in its final stages. When the core becomes a White Dwarf the star eventually cools and dims. When it stops shining, it becomes a dead star and is called a Black Dwarf.
2.) Shown below is a Hertzsprung-Russell Diagram. The following data is available for a star X with respect to the Solar mass (M0) and the Solar Radius (R0):
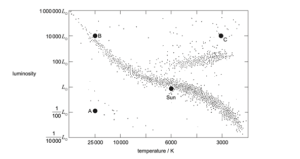
Mx = 4.7 M0
Rx = 3.4 R0
a.) By how much is the luminosity of the star X greater than the luminosity of the sun
Answer
Lx = 4.73.5 M0 since the relationship between luminosity and mass is L = M3.5
Therefore, 4.73.5 = 225 L0
b.) The parallax angle of star X from Earth is 0.174 arc second. Outline how the parallax angle of a star can be measured
Answer
The position of a star is recorded in a 6 month gap (Month 1 and Month 7). The parallax angle is calculated by seeing how much the star has moved relative to the distant stars present in the background.
c.) Star X eventually becomes a White Dwarf.
i.) State the star type for A, B and C
Answer
A: White Dwarfs
B: Main sequence
C: Red Giant
ii.) State what prevents Star X from collapsing further after becoming a white dwarf
Answer
An electron degeneracy. Electron degeneracy pressure will halt the gravitational collapse of a star if its mass is below the Chandrasekhar limit (1.44 solar masses) which it is since we’re talking about the Sun here. This is the pressure that prevents a white dwarf star from collapsing.
3.) Light from a galaxy far away observed on Earth shows a redshift of 0.13.
a.) Define redshift
Answer
Redshift is when the wavelength of the light is stretched, so the light is seen as ‘shifted’ towards the red part of the spectrum. It means that the received wavelength is longer than the emitted wavelength.
b.) Determine the distance to this galaxy using the Hubble Constant assuming that it is H0 = 67 (km/s)/Mpc
Answer
First the velocity needs to be determined using the formula v = zc where z is the redshift and c is the speed of light. Therefore, substituting the respective values, we have: v = 0.13 x 3.0 x 105 = 3.9 x 104 km/s. To find the distance, the formula d = v / H0 can be used. Putting in the values, we have, d = 3.9 x 104 / 67 = 582 Mpc
c.) Suggest how the cosmic microwave background radiation provides strong evidence for the existence of the Big Bang model.
Answer
The CMB radiation is essentially a black body spectrum that is highly isotropic across the universe. The wavelength of this CMB radiation matched the predicted wavelength of the Big Bang had it increased by expansion.
4.) The question is with regards to planets and stars
a.) 4 of the outer planets in the solar system are Jupiter, Saturn, Uranus and Neptune
i.) List these planets in order of increasing distance from the Sun
Answer
Jupiter, Saturn, Uranus, Neptune
ii.) List these planets in order of increasing mass
Answer
Uranus, Neptune, Saturn, Jupiter
b.) Define apparent brightness and luminosity
Answer
Apparent brightness is a measure of the amount of light received by Earth from a star or other object. Luminosity is an absolute measure of the radiant power emitted by a light-emitting object.
c.) The apparent brightness of a Star C is 3.4 x 10-10 W/m2. The luminosity of the Sun is 3.9 x 1026 W. Determine the distance of C from Earth
Answer
The formula used here is d = (L / 4πb)½
Substituting the values we have, d = (3.9 x 1026 x 104 / 4π x 3.4 x 10-10)1/2
d = 3.02 x 1019 m
References:
Our Expert Tutors!
- 12+ Years
Cat 1 – ESS and Cat 2 – Biology. Chief of the IB program. Mentored 320+ students across various curricula.
- 24+ Years
IBDP Physics HL / SL. IGCSE Physics. A-level Physics (AQA, CIE, Edexcel, OCR, and WJEC). IGCSE Physics (AQA,CIE, OCR & Edexcel)
- 9+ Years
IBDP Cat 1 – Business Management, IBDP Cat 1 – TOK. Taught over 130+ students across 4+ countries.
- 9+ Years
IBDP Cat 1 & 2 November 2019. Specializes in Global Politics. Many students scored 7s; mentors 200+ students in assessments.
- 16+ Years
Specializing in Mathematics: Analysis and Approaches (HL & SL), Mathematics: Applications and Interpretation (HL & SL), and MYP (Mathematics).
- 18 + Years
IBDP Cat 1 – Chemistry, IBDP Cat 3 – IA Chemistry, IBDP Cat 1 – TOK. Helped 2 out of 3 students achieve a 7 in IB Chemistry.












