equilibrium Notes
Equilibrium
Equilibrium reactions in chemistry
- Many important chemical reactions are reversible and exist in a state of equilibrium, with both the forward and reverse reactions occurring simultaneously with products and reactants constantly being interconverted.
- Suppose we have hot liquid in a storage container sealed with a lid. Water molecules in the liquid that have sufficient energy will leave the liquid phase and enter the gaseous phase in the process of evaporation.
- At the same time, some gaseous water molecules will lose energy through collision and enter the liquid phase in the process of condensation.
- Eventually the rate of evaporation will equal the rate of condensation and there will be no further change in the amount of liquid present and the amount of gas present in the closed system.
- The concentration of liquid and gas does not change, but molecules are constantly being interconverted between the two phases. This is described as a dynamic equilibrium.
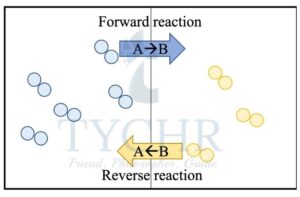
Figure 1: In a dynamic equilibrium the forward and reverse reactions occur at equal rates.
Chemical systems
- In reality many reactions exist in a state of equilibrium.
- The relative rates of forward and reverse reactions depend on the physical conditions of temperature and pressure, on chemical conditions (a change in concentration of reactants and products), and in the presence of a catalyst.
- Nitrogen(IV) oxide or nitrogen dioxide, NO2 is a toxic brown gas that exists in equilibrium with colourless dinitrogen tetroxide, N2O4: N2O4(g) ⇋ 2NO2(g)
- Initially the rate of decomposition of N2O4 will be greatest, when the concentration [N2O4] is at a maximum. As time passes, sufficient NO2 molecules will be present in the closed system for successful collisions to reform N2O4.
- The concentration of N2O4 decreases progressively while the concentration of NO2 The system approaches a dynamic equilibrium as the rates of the forward and reverse reactions become equal.
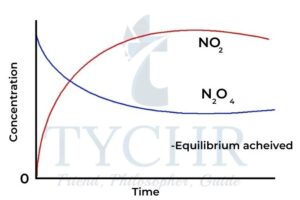
Figure 2: Change in concentration versus time for the reaction N2O4(g) ⇋ 2NO2(g) approaching and achieving equilibrium 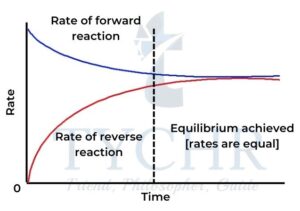
Figure 3: At equilibrium, the rates of the forward and reverse reactions remain constant.
At equilibrium:
- The forward and reverse reactions are occurring at equal rates.
- There is no change in the concentrations of reactants and products.
- There is no change in macroscopic properties such as colour and density.
- The equilibrium can be approached from either the forward or reverse direction.
- The equilibrium is dynamic. The forward and reverse reactions continue but no overall change in the concentration of reactants and products occurs.
- Any changes in the reaction conditions, such as temperature, pressure, or concentration of reactants or products, can affect the equilibrium, demonstrating its dynamic nature.
The equilibrium law
- The law of chemical equilibrium states that at a given temperature the ratio of the concentration of products (raised to the power of their molar coefficients) to the concentration of reactants (raised to the power of their molar coefficients) is a constant.
- This constant is called the equilibrium constant, Kc. The subscript ‘c’ indicates that concentration values for products and reactants are being used.
- For example: H2(g) + I2(g) ⇋ 2HI(g)

- For the reaction: aA + bB ⇋ cC + dD
- The equilibrium constant expression is Kc = ([𝐂]𝐜[𝐃]𝐝/[𝐀]𝐚[𝐁]𝐛)
- The equilibrium constant expression has the concentrations of products in the numerator and the concentrations of reactants in the denominator.
- Each concentration is raised to the power of its coefficient in the balanced equation.
- Where there is more than one reactant or product the terms are multiplied together.
Kc for the inverse reaction
- The inverse reaction cC + dD ⇋ aA + Bb
Defines the products as reactants and vice versa. We will denote its equilibrium constants as KC’.
KC’ = ([𝐀]𝐚[𝐁]𝐛/[𝐂]𝐜[𝐃]𝐝)
We can see that KC’= 1/KC
Kc for a multiple of a reaction
- Consider the reaction: 2aA + 2bB ⇋ 2cC + 2dD
We will denote its equilibrium constant KCX.
KCX = ([𝐂]2c[𝐃]2d/[𝐀]2a[𝐁]2b)
Change in reaction equation | Equilibrium constant expression | Equilibrium constant |
reverse the reaction | inverse of the expression | 1/KC or KC’ |
halve the coefficients | square root of the expression | √ 𝐊c |
double the coefficients | square the expression | KC2 |
sum equations | product of the expressions | Kc = Kc1 × Kc2 × … |
Table 1: The equilibrium constant Kc for the same reaction at the same temperature can be expressed in a number of ways
The effect of changing experimental conditions on the equilibrium constant
- When equilibrium is established, the position of the equilibrium remains constant provided that the temperature and pressure do not change.
- A change in experimental conditions can affect the equilibrium position.
- However, the value of Kc remains constant unless the temperature changes.
Change in condition | Equilibrium position | Kc |
concentration of product or reactant | changes in response to a change in reactants or products | no change |
pressure | in a reaction with gaseous reactants or products, the pressure can affect the equilibrium position | no change |
temperature | usually changes: the direction of change depends on whether the reaction is exothermic or endothermic | changes, unless |
catalyst | no change | no change |
Table 2: The effect of changing conditions on the equilibrium position and the value of Kc
Reaction quotient
- If a system has not reached equilibrium, the ratio of concentration of product to reactants will not equal K.
- This ratio is called the reaction quotient Q and this helps you to determine the progress of the reaction as it moves toward equilibrium and the direction of the reaction that is favoured to establish equilibrium.
Q > Kc | The concentration of products is greater than at equilibrium and the reverse reaction is favoured until equilibrium is reached. |
Q < Kc | The concentration of reactants is greater than at equilibrium and the forward reaction is favoured until equilibrium is reached. |
Q = Kc | The system is at equilibrium and the forward and reverse reactions occur at equal rates. |
Table 3: The relationship between the reaction quotient Q and the equilibrium constant Kc
The equilibrium law
Calculating the equilibrium constant using concentration data
- To calculate the equilibrium constant Kc for a reaction at a given temperature, we follow a series of steps using initial concentrations and equilibrium concentrations.
1.) Deduce the balanced chemical equation for the reaction.
2.) Arrange the data according to the ICE method:
I: Initial concentration of the reactants. Initially, products = 0.
C: Change in concentration. This is the amount by which [reactants] decrease and products increase. These changes must be consistent with the stoichiometric ratios shown by the coefficients in the balanced equation.
E: Equilibrium concentration is the concentration of reactants and products when equilibrium is established.
3.) Substitute the values into the equilibrium constant expression and determine the equilibrium constant. - For example: 2SO2 (g) + O2 (g) ⇋ 2SO3 (g)
I | 2.0 | 1.4 | 0.0 |
C | -2α | -α | +α |
E | 1.7 | 1.25 | 0.30 |
- The conversion rate of 15% means that 15% of SO2 is converted into products. Hence the equilibrium amount for SO3 will be: 2.0 × 15% = 0.30
α can then be found as : 0.30 = +2α ; α = 0.15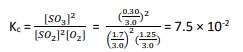
Gibbs free energy and equilibrium
- When the equilibrium constant K is determined for a given reaction, its value indicates whether products or reactants are favoured at equilibrium.
- The Gibbs free energy change ∆G for a given reaction is an indication of whether the forward or reverse reaction is favoured.
- At a given temperature, a negative ∆G value for a reaction indicates that the reaction is spontaneous and the equilibrium concentrations of the products are larger than the equilibrium concentrations of the reactants.
- The equilibrium constant is greater than 1. The more negative the value of ∆G, the more the forward reaction is favoured and the larger the value of K.
- The quantitative relationship between standard Gibbs free energy change, temperature, and the equilibrium constant is described in the equation:
∆G = -RT ln K
ln K = ∆G/RT
Equilibrium Constant | Description | Gibbs free energy change |
K=1 | at equilibrium, neither reactants nor products favoured | ∆G=0 |
K>1 | products favoured | ∆G < 0 (negative value) |
K<1 | reactants favoured | ∆G > 0 (positive value) |
Table 4: The relationship between the equilibrium constant and the Gibbs free energy change

