Exponential and Logarithmic Functions Notes
INTRODUCTION
- Exponents- A quantity representing the power to which a given number or expression is to be raised. Ex.- 53=5×5×5 (53 is read as ‘five raised to the power three’ or ‘Five to the third power’)
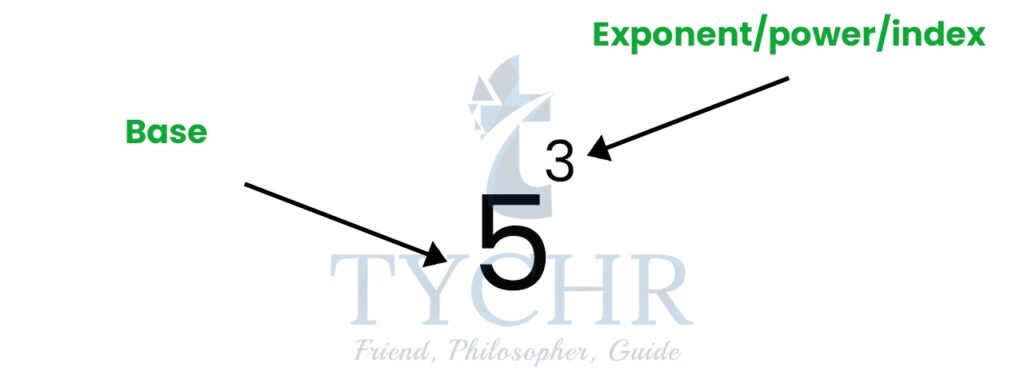
- Exponential Functions- It involves powers, where an independent variable is used as an exponent. E.g. f(x)=ax, f(x)= 42x
When ‘a’ is replaced by ‘e’ in the first example, we get f(x)=ex, which is known as Natural Exponential Function or simply The Exponential Function. - Logarithms- They let us undo the exponential effects. They are a convenient way to express large numbers.
E.g. Consider 62=36, when this equation is written in logarithmic form, we get:
- Logarithmic Functions- It can be explained by taking an example of exponential function and converting it to logarithmic function.
Consider y=ax, then the corresponding logarithmic function will be logay=x
LAWS OF EXPONENTS
- Multiplication with same bases : am×an=a(m+n)
- Division with same bases am/an= am+n
- Power of Zero a0=1,a≠0
- Negative Exponents a-m = 1/ am
- Raising a power to a power (am)n =amn
- Fractional Exponents 𝑎(𝑚⁄𝑛) = 𝑛√𝑎m
Example:
a.)Simplify ) (5×𝑡8×𝑡−2)/(𝑡2×𝑡4)
Solution: (5×𝑡8×𝑡−2)/(𝑡2×𝑡4) Applying Law 1 to numerator and denominator: (5×𝑡8−2)/(𝑡2+4) = (5×𝑡6)/(𝑡6)
Applying Law 2:
5t(6-6)
5t0Applying Law 3:
5×1=5
Ans= 5
b.) 4(𝑝2×𝑝3)6/5/4√𝑝8
Solution: 4(𝑝2×𝑝3)6/5/4√𝑝8
Applying Law 1 to numerator:
4(𝑝5)6/5/4√𝑝8
4(𝑝5×6/5/𝑝8/4)Applying Law 5 to numerator and Law 6 to denominator:
4(𝑝5×6/5/𝑝8/4) = 4(𝑝6/𝑝2)
Applying Law 2:
4p4
Ans: 4p4
EXPONENTIAL FUNCTIONS
CHARACTERISTICS
There shouldn’t be any confusion between a Power Function and an Exponential function.
y=x2 is a power function with base as the variable.
y=2x is an exponential function with power as the variable.
Note:
- The domain of all Power Function is all Real numbers, which eventually leads us to the domain of all Exponential Functions being all Real Numbers as well.
(This idea will be clearer when we’ll discuss graphs) - It is evident in the following table that the increase and decrease in an Exponential Function is at much faster rate than a Power Function.
x | x2 | 2x |
4 | 16 | 16 |
5 | 25 | 32 |
6 | 36 | 64 |
7 | 49 | 128 |
8 | 64 | 256 |
9 | 81 | 512 |
GRAPHS OF EXPONENTIAL FUNCTIONS
The domain of an exponential function is all Real numbers; hence the graph will be continuous.
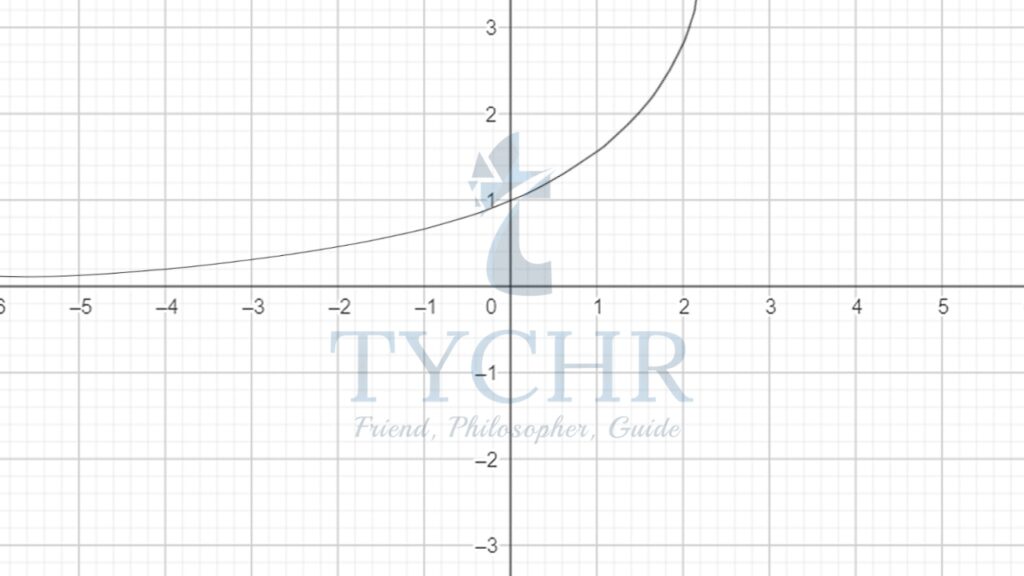
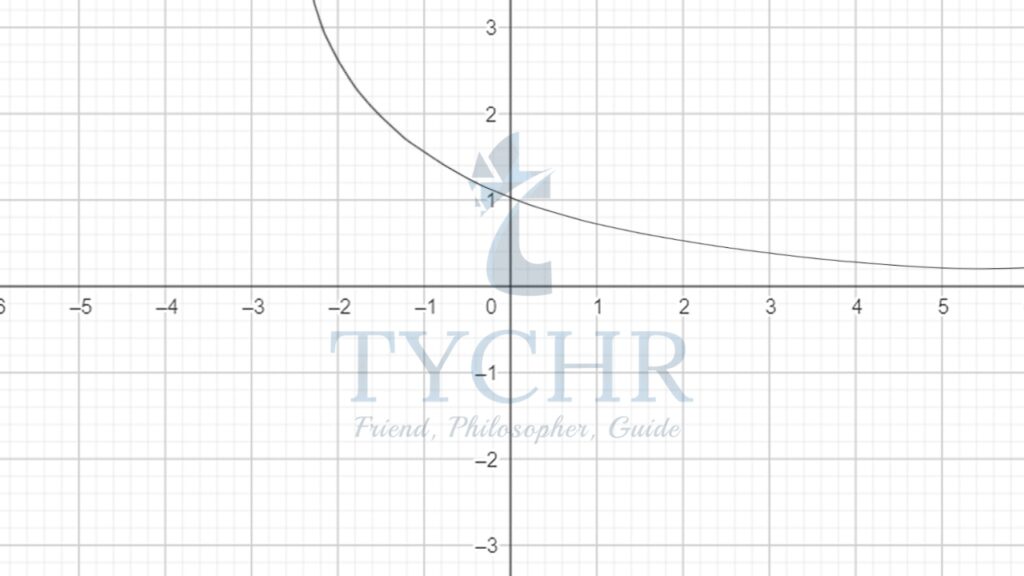
Graph of f(x)=ax for a>1 Graph of f(x)=ax for 0<a<1
f(x)→0 as x→-∞ f(x)→0 as x→∞
f(x)→∞ as x→∞ f(x)→∞ as x→-∞
For the functionf(x)=ax, the domain is x ϵ R and the range is the set of all positive real numbers (y>0). The graph passes through (0,1) (as any number to the power zero is 1)
Asymptote- A straight line that continually approaches a given curve but does not meet it at any finite distance.
In the above two graphs, x-axis is the horizontal asymptote.
When a>0 there is a continually increasing Exponential Growth Curve continually and when 0<a<1 there is a continually decreasing Exponential Decay Curve.
TRANSFORMATION OF GRAPHS
Taking examples for each kind of transformation:
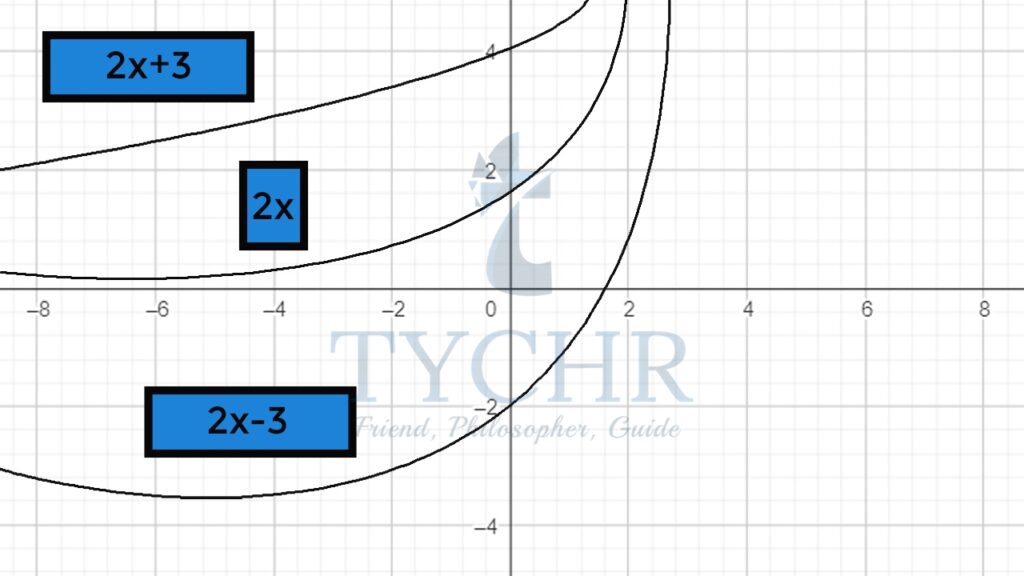
a. 2x±3
The graph of 2x moves three units vertically up when 3 is added and moves three units vertically down when 3 is subtracted.
Function | Asymptote |
y=2x | y=0 |
y=2x +3 | y=3 |
y=2x -3 | y=-3 |
Function | Domain | Range |
y=2x |
|
|
y=2x +3 |
|
|
y=2x -3 |
|
|
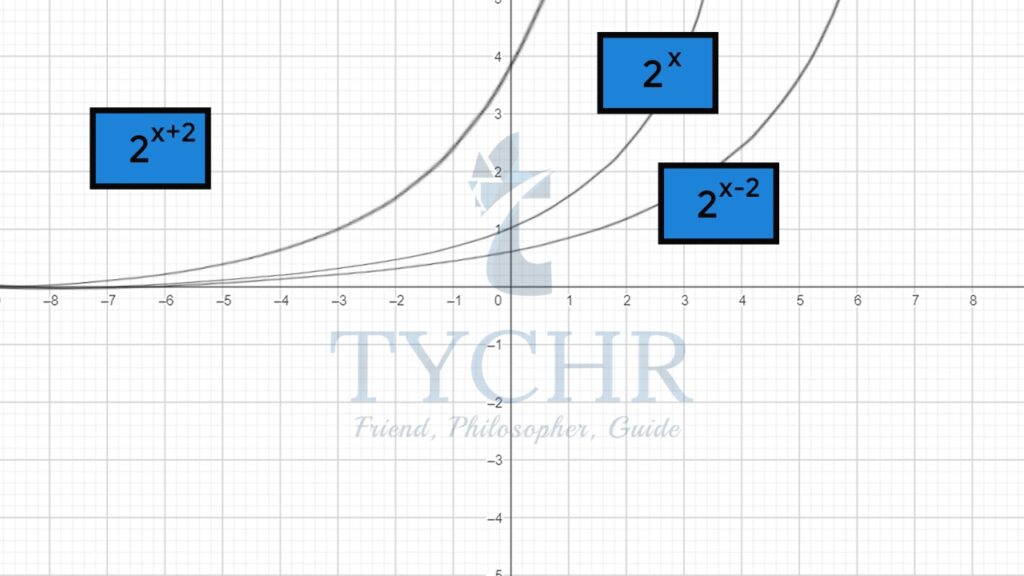
b. 2(x±2)
The graph of 2x moves two units horizontally left when 2 is added and moves two units horizontally right when 2 is subtracted.
The asymptote will remain the same, i.e. y=0
The domain and range of all three functions in the graph here will be same:
Domain- ]-∞,∞[
Range- ]0,∞[
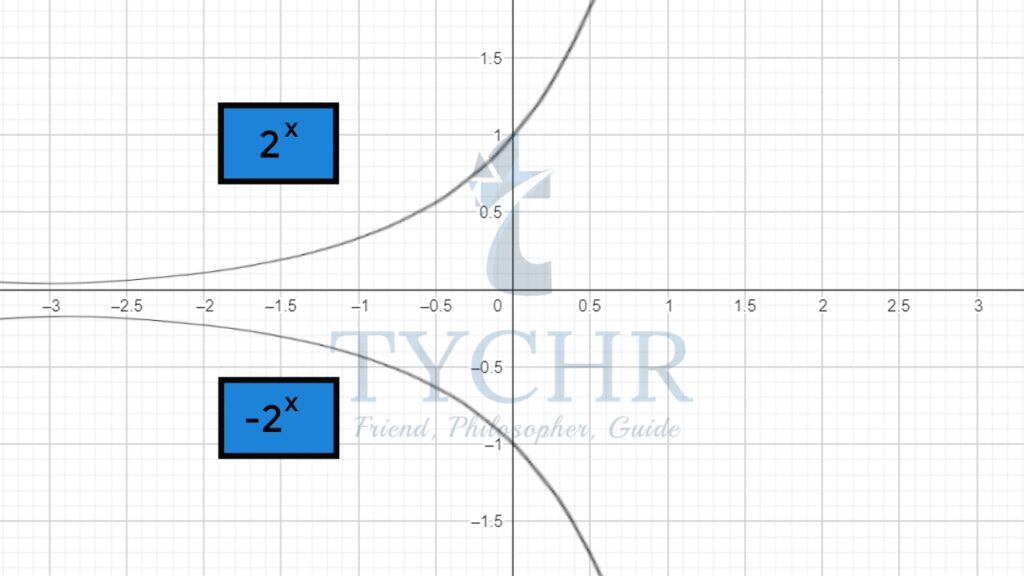
c. ±2x
The graph of -2x is the reflection of 2x in the x-axis.
The asymptote will remain the same, i.e. y=0
Function Domain Range
Function | Domain | Range |
y=2x | ]-∞,∞[ | ]0,∞[ |
y=-2x | ]-∞,∞[ | ]-∞,0[ |
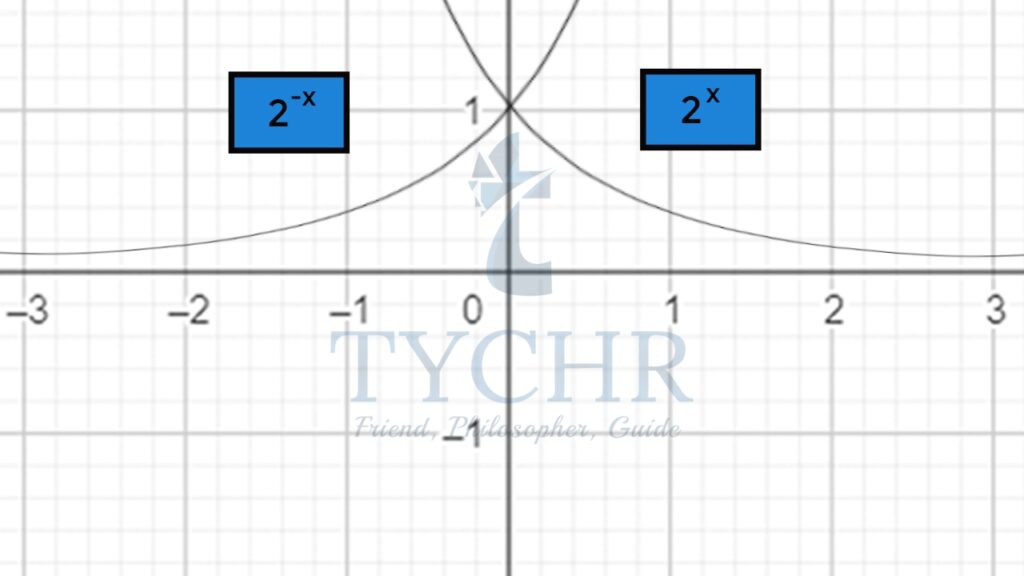
d. 2(±x)
The graph of 2(-x) is the reflection of the graph 2x in y axis.
The asymptote will remain the same, i.e. y=0
The domain and range of the functions in the graph here will be same:
Domain- ]-∞,∞[
Range- ]-0,∞[
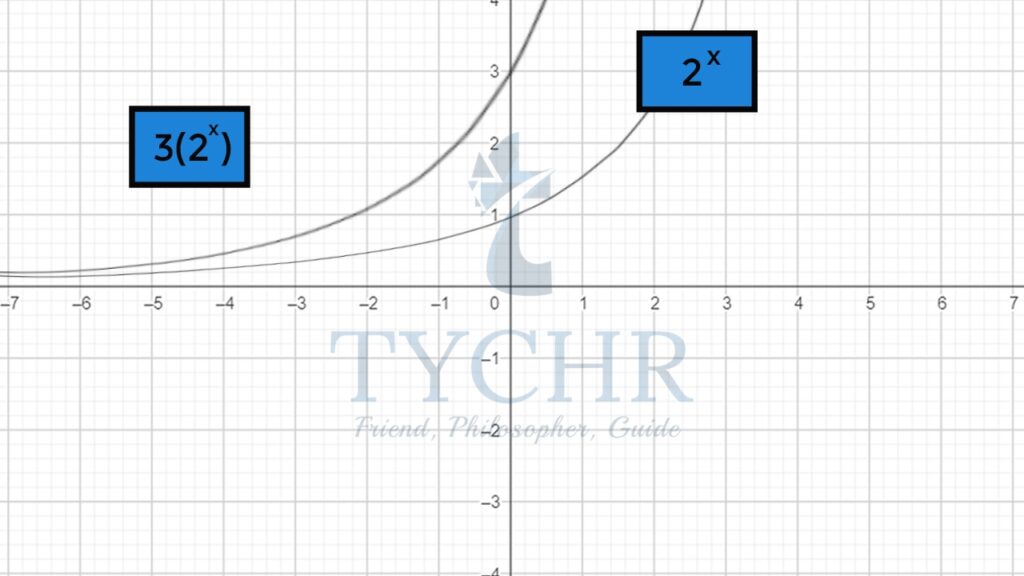
e. 3(2x )
The graph of 3(2x ) can be obtained by the vertical sketch of the graph of 2x , by a scale factor of 3.
The domain and range of the functions in the graph here will be same:
Domain- ]-∞,∞[
Range- ]0,∞[
EXPONENTIAL GROWTH AND DECAY
Taking a few general examples to understand:
Corona Virus patients grew from a few hundreds to millions in a very short period of time. This kind of growth is what we call Exponential Growth.
Examples of Exponential Decay are Radioactive decay, decay of sound when a bell is struck etc.
We have a general formula for Exponential Growth/Decay: y(t)= a × ekt
Where, y(t) = value at time ‘t’
a= Value at the start
k= Rate of growth/decay
t= Time
Example: The value of a boat, y, in thousand of UK pounds is modelled by the function y=20(0.8)x, where ‘x’ is the number of years since it was manufactured.
Find the value of boat when it was brand new
Estimate the value of the boat when it is 3 years old
Estimate the time in years when it will be worth half of its original price
Solution:
At x=0, we will get the value of boat when it was brand new.
y=20(0.8)x
Putting x=0
y=20
Hence, the value of the brand new boat was 20 thousand pounds.
For the value of boat after 3 years, we put x=3 in the function y=20(0.8)x, we get:
y=20(0.8)3=10.24
Hence, the value of boat after 3 years will be 10.24 thousand pounds.
The original price was 20 thousand pounds; we need the time in years when the price was half i.e. 10 thousand pounds.
We put y=10 in the function y=20(0.8)x we get:
10=20(0.8)x
0.5=(0.8)x
Solving by trial and error, we get:
x=4.27
Hence, after 4.27 years, the boat will be worth half of its original price.
EULER’S NUMBER (e)
The number ‘e’ is one of the most important numbers in mathematics.
It is an irrational number, with an approximate value of 2.718281….
A log with base as ‘e’ is known as the natural log. Denoted by logex or lnx.
It can be used to model growth or decay of a quantity that is changing exponentially when the change is continuous or approaching continuous.
To understand what this number ‘e’ is and how we obtain its value, we will compute amounts of money resulting from an initial amount (principle) with interest being compounded at discrete intervals. Consider the formula for the amount of money: A = P(1 + (1/r))nt
A= Amount of money after adding the interest
P= Principle or initial amount of money
r= Interest rate
n= Number of times interest applied per time period
Considering Principle amount to be £1
And rate of interest be 100%
Compounded annually
A=1(1+1)1
A=£2
Compounded half yearly
A = P(1 + (1/2))12
A=£2.25
Compounded every month
A = P(1 + (1/12))12
A=£2.61
Compounded everyday
A = P(1 + (1/364))364
A=£2.714567…
Compounded every minute
A = P(1 + (1/(365x24x60)))365x24x60
A=£2.718…
Look carefully and observe that as we increase the number of times interest is applied, we get closer and closer to the number ‘e’.
Mathematically when we use ∞ in place of ‘n’, we get the value of the number ‘e’. We cannot evaluate this value without the use of limit, therefore we get:
e = (1 + (1/n))n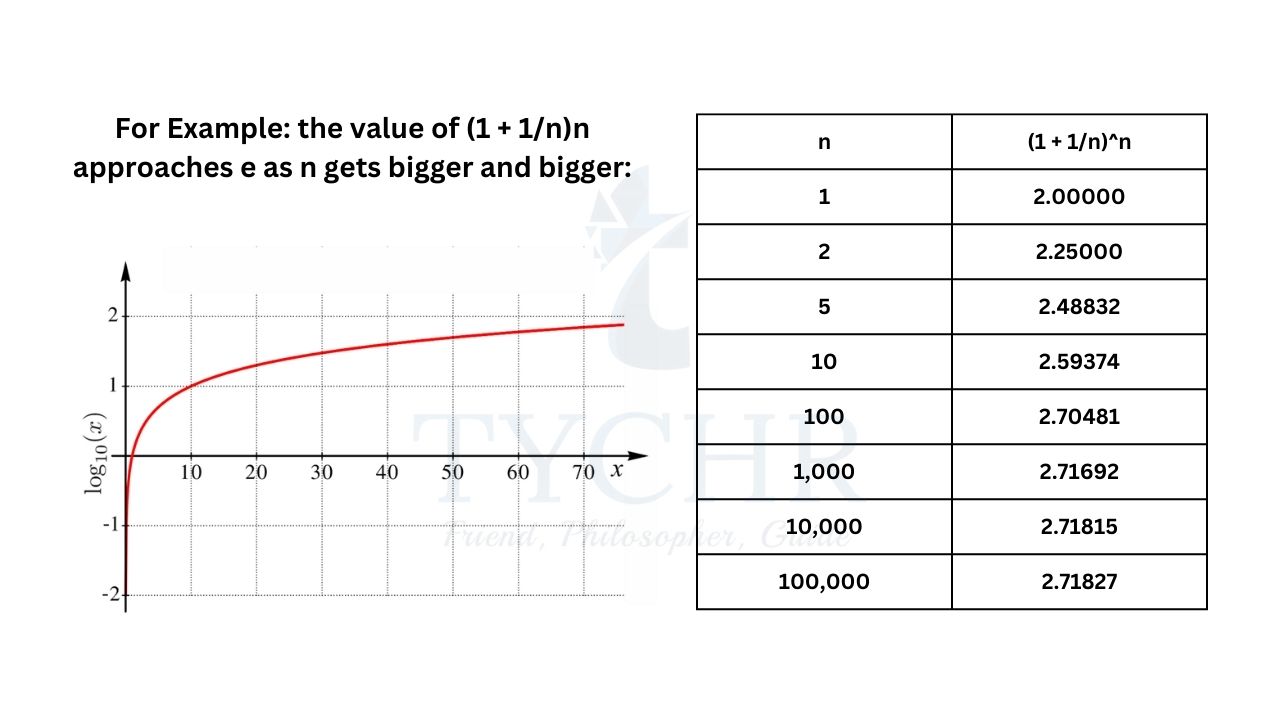
LOGARITHMIC FUNCTIO
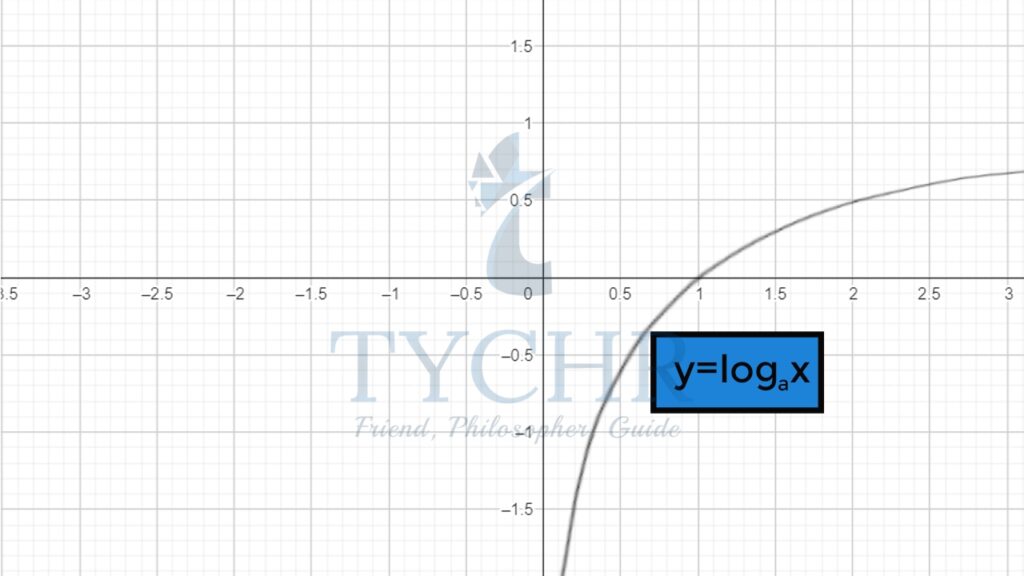
Taking a logarithmic function y=logax.
For a>0,a≠1
x=0 is an asymptote
Cuts the x- axis at (1,0)
The graph increases continually
Domain- All positive real numbers
Range- All real numbers
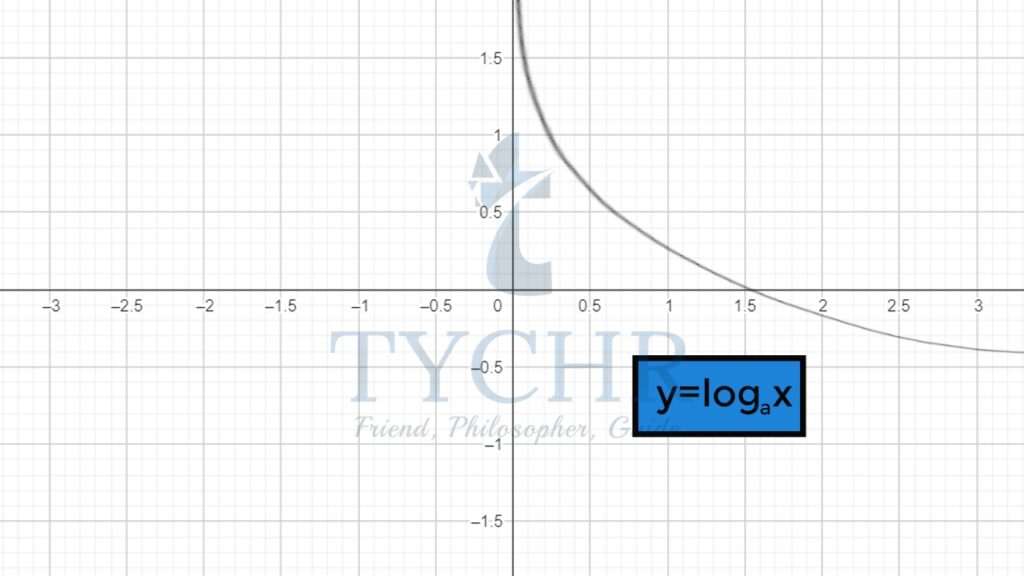
For a<0,a≠1
x=0 is an asymptote
Cuts the x-axis at (1,0)
The graph decreases continually
Domain- All positive real numbers
Range- All real numbers
The transformation of graphs of logarithmic functions will be same as that we learnt for exponents.
LOGARITHMIC EXPRESSIONS AND EQUATIONS
Recall the meaning of a logarithmic expression. Taking the same example again, 62=36 can be written as log636 =2.
This means that the value of log636 is the exponent to which 6 must be raised to obtain 36. Hence, the answer is 2.
Similarly a logarithmic equation can be converted into an exponential equation.
Example- log101000=3, when written in exponential form will become- 103=1000.
The logarithmic function with base 10 is called Common Logarithmic Function (denoted by log). And when ‘e’ is used as a base, then we call it the Natural Log (denoted by ln).
INVERSE OF EXPONENTIAL FUNCTION
Exponential function is a one-one, onto function, by definition. Hence, it can be inverted.
Taking f(x)=ax
Then, f(-1) (x)=logax
y=f(-1) (x) is a reflection of y=f(x) in the line y=x
This concept also confirms the domain and range of logarithmic functions.
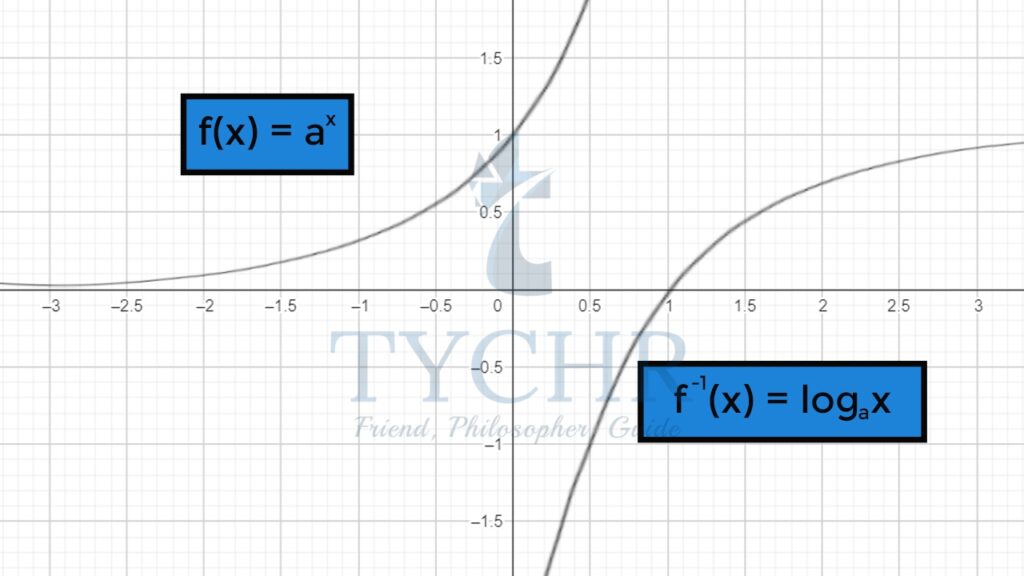
Notice that the points (1,0) and (0,1) are mirror images of each other in the line y=x.
PROPERIES OF LOGARITHMS
Property 1
logaax =x
This equation says- what should ‘a’ be raised to, to obtain ‘ax’. And clearly the answer is ‘x’
Property 2
loga(MN)=logaM+logaN
Let loga(M)=x and loga(N)=y
Then we have M=ax and N=ay
Now loga(MN)=loga(axay)
Using Law 1 of exponents:
loga(MN))=loga(a(x+y))
Using Property 1 of logarithms:
loga(MN)=x+y
Putting values of x and y
Therefore,loga(MN)=logaM+logaN
Property 3
loga(M/N)=logaM – logaN
Let loga(M) = x and logaN = y
Then we have M=ax and N=ay
Now loga(M/N)=loga(a(x-y))
Using Law 2 of exponents:
loga(M/N)=loga(M/N)
Using Property 1 of logarithms:
loga(M/N)=x-y
Putting values of x and y
Therefore, loga(M/N)=logaM – logaN
Property 4
loga(Mk )=k logaM
Substitute M=ax
We get:
loga(Mk )=loga((ax)k )
loga(Mk )=loga(axk )
Using property 1 of logarithms:
loga(Mk )=xk
Now, we know that x=logaM
Therefore, loga(Mk )=k logaM
Property 5
alogax =x
Put logax=m or am=x
Then, alogax =am
Therefore, alogax =x
Property 6
logba=logma/logmb
Let y=logba
In exponential form – a=by
Solving the LHS
logma/logmb =logmby /logmb
Using property 1 of logarithms:
logma/logmb =y
Therefore, log_ba=log_ma/log_mb
This property is also called, Change of Base.
Examples:
Find the value of log232
32 can be written as 25
Therefore, log232=log225
Using property 1 of logarithms:
log532=5
Ans- 5
Express as sum of logarithms: logb(x3/y2 )
Using property 3 of logarithms:
logbx3 -logby2
Using property 4
3 logbx-2 logby
Ans- 3 logbx-2 logby
Convert into logarithm of single quantity: log3M+log3N-2 log_3P
Using property 2 in first 2 terms:
log_3〖(MN)-2 log_3P 〗
Using property 4:
log3(MN)-log3P2
Using property 3:
log3(MN/P2)
Ans-log3(MN/P2)
Find the value of log_320 by converting to base 10.
Using property 6:
log320=log20/log3 (log written without base is assumed to be as log with base 10)
log320=log(2×2×5)/log3
Using property 2 and 3:
log320=( log2+log2+log5)/log3
Using previously mentioned values of log with base 10:
log320=(0.301+0.301+0.698)/0.477
log320=2.73
Ans- 2.73
SOLVING EXPONENTIAL EQUATIONS
We will use properties of logarithms to solve exponential equations. But first we will need to convert an exponential equation to a logarithmic one.
Instead of going by definition we take log with base 10 or with base as any other number or variable or ln (depending upon the question) on both the sides of the equation and then solve.
i.e. if m=n then log_am=log_an (a>0)
Examples:
Use logarithms to solve 5(1-x)=50
Taking log with base 10 on both the sides:
log10(5(1-x)=log1050)
Using property 4 of logarithms:
(1-x)log10(5=log10(5×5×2)
(1-x) log5=log5+log5+log2
Putting the values of log as mentioned before:
(1-x)0.698=0.698+0.698+0.301
x=-0.715
Ans- -0.715
Solve for x in the equation 32x-18=3(x+1)
32x-(3)(3)x)-18=0
Putting 3x=y
y2-3y-18=0
Splitting the middle term:
y2-6y+3y-18=0
y(y-6)+3(y-6)=0
(y-6)(y+3)=0
y=6 or y=-3
Therefore,
3x=6 or 3x=-3
3x=-3 is not possible, because we cannot raise a power to a positive number to get a negative number.
So we continue with 3x=6
Taking ln on both the sides:
ln(3x=ln6
Using property 4 of logarithms:
x ln3=ln6
x=ln6/ln3
Ans- ln6/ln3
SOLVING LOGARITHMIC EQUATIONS
We can solve Logarithmic Equations by applying the basic definition of logarithm and its properties.
Example: Solve for x, log2x+log2(10-x)=4
Using property 2 of logarithms:
log2(x)(10-x)=4
log2(10x-x2)=4
Using the basic definition of log and converting it to exponential form:
10x-x2=24
x2-10x+16=0
x2-8x-2x+16=0
x(x-8)-2(x-8)=0
(x-8)(x-2)=0
x=8 or x=2
We need to check if both solutions are valid. Putting them in the parent equation we see that both of the solutions hold true.
Ans- 2,8
We can solve Logarithmic Equations in another way. Here is an example to understand:
Example: Solve for x, ln(x-2)+ln(2x-3)=2 lnx
Using property 2 and 4 of logarithms:
ln{(x-2)(2x-3)}=lnx2
ln(2x2-7x+6)=lnx2
Exponentiate both sides:![]() Using property 5 of logarithms:
Using property 5 of logarithms:
2x2-7x+6=x2
x2-7x+6=0
x2-6x-x+6=0
x(x-6)-1(x-6)=0
(x-6)(x-1)=0
x=6 or x=1
If we put x=1 in the parent equation, we get a negative number inside a logarithm, which does not satisfy the domain (domain of logarithm is all positive real numbers).
Hence the only solution of the given equation is x=6
Ans- 6
DERIVATIVE OF EXPONENTIAL FUNCTIONS AND NATURAL LOGARITHMIC FUNCTION
If f(x)=ex, then f‘(x)=ex
This is a very interesting result.
We know that the derivative of a function is the slope of the tangent line at that particular point. The derivative and the function being the same, implies that the slope of the tangent line at any point is equal to the function!
If f(x)=lnx, then f(x) = 1/x
Example: Find the derivative of- f(x)=5ex+2 lnx
Using the above 2 results:
f(x) = 5ex + (2/x)
Ans: 5ex + (2/x)
