Functions Equations and Inequalities Notes
By the end of this chapter, you should be familiar with:
- Quadratic functions and different forms in which to express them.
- Finding characteristics of parabola
- Solving quadratic equations and inequalities
- Applying the quadratic formula
- Rational functions and their graphs
QUADRATIC FUNCTIONS
A linear function is a polynomial function of degree one, which were discussed in the previous chapter.
In this section we will focus on quadratic functions which are expressed as a second-degree polynomial that can be written in the form f(x)=ax2+bx+c, where a≠0.
In last chapter we studied transformations of functions, now we will further study the graphs of quadratic functions. A parabola represnts a quadratic function.
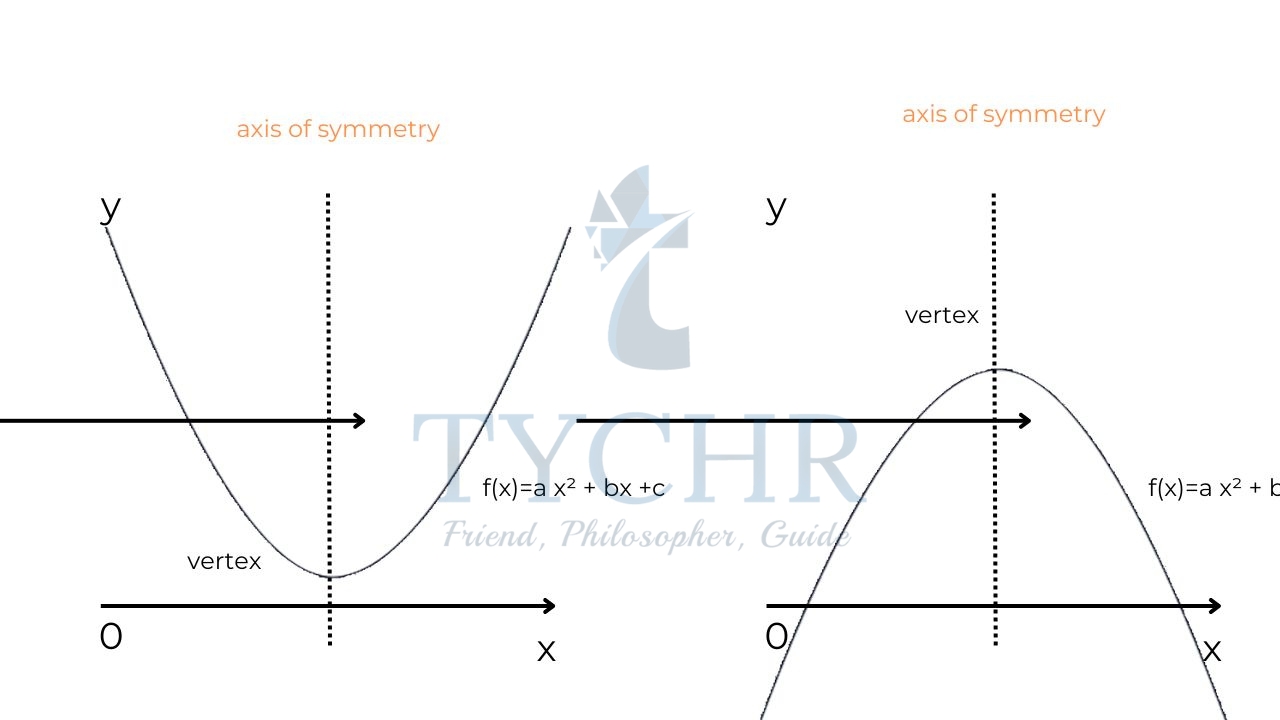
The key features of a parabola are:
Axis of symmetry- Every parabola has symmetry about a vertical line, called axis of symmetry
Vertex- The axis of symmetry passes through a point on the parabola called vertex.
Concavity- If the leading coefficient a, of the quadratic function is positive, then the parabola opens upwards (concave up) and the y-coordinate of the vertex is the minimum value of the function. If the leading coefficient a, of the quadratic function is negative, then the parabola opens downwards (concave down) and the y-coordinate of the vertex is the maximum value of the function.
THE GRAPH OF 𝒇(𝒙) = a(x-h)2 + k (VERTEX FORM)
We know how to transform a graph from previous chapter.
f(x) = ax2 + bx + c is known as the vertex form. We know the graph of y=x2, it can be transformed into 𝒇(𝒙) = a(x-h)2 + k by a series of transformation which we are familiar with.
Taking an example- 𝒇(𝒙) = (x – 2)2 – 5
We can above the above graph, by shifting the graph of y=x2, two units to the left and five units down.
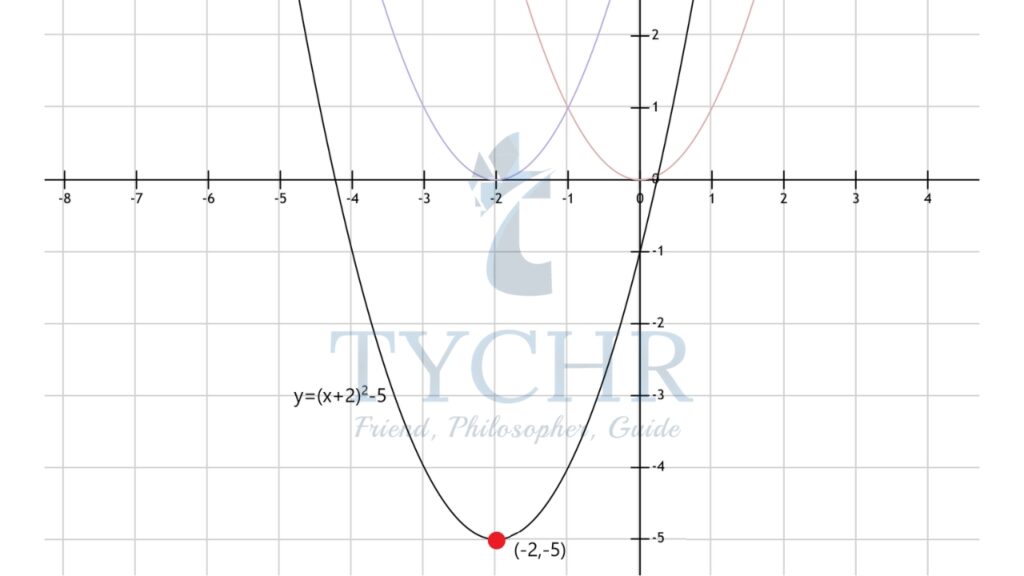
Looking at the graph, we see the vertex lies at (-2,-5). Which we can figure out directly from the equation.
If the equation is 𝒇(𝒙) = a(x-h)2 + k, then the vertex will be at(h,k). Hence, this form of equation is called the vertex form.
So instead of transforming the graph, we can simply find the vertex, x and y-intercept, and sketch the graph.
The vertex form can be solved and converted to general form (ax2+bx+c), and the general form can also be converted to vertex form, which we will learn in the next section.
COMPLETING THE SQUARE
General form can be converted to vertex form by completing the square method. It is useful because a equation in vertex form is easier to graph, as we learnt in the previous section.
We have general form – ax2+bx+c, to convert this equation to vertex form, we need a perfect square.
Instead of using formulas, lets take examples and understand:
Ex. f(x)=x2-8x+18
We know that (a+b)2 = a2 +2ab + b2
f(x) = x2 – 2(4)(x) + 18 The middle term is our 2ab term, now we add and subtract our b2 term: f(x) = (x2 – 2(4)(x) + 42 ) + 18 -42 We have developed a perfect square!
f(x) = (x-4)2 + 18 -16, f(x) = (x-4)2 + 2 which is our vertex form.
Ex. Find the equation of axis of symmetry, the coordinates of the vertex, the y-intercept and the maximum or minimum point and also sketch the graph. f(x)=-x2+6x-4
First, converting to vertex form:
f(x)=-x2+6x-4
f(x)=-(x2-6x+4)
f(x)=-(x2-2(3)(x)+32+4-32)
f(x)=-((x-3)2-5)
f(x)= -(x-3)2+5)
The sign of the first coefficient is negative, so the parabola will be concave down.
Comparing to vertex form, f(x)=a(x-h)2+k, the vertex of the parabola is (h,k), which in this case will be (3,5)
The axis of symmetry is a vertical line passing through the vertex, therefore the equation of axis of symmetry will be x=3.
For y-intercept, putting x=0 in f(x), we get: y = -(-3)2 + 5
y=-4
So the y-intercept is (0,-4)
The graph is concave down, therefore the y-coordinate of the vertex is the maximum point of the function i.e. y=5.
Using this information, graphing the function: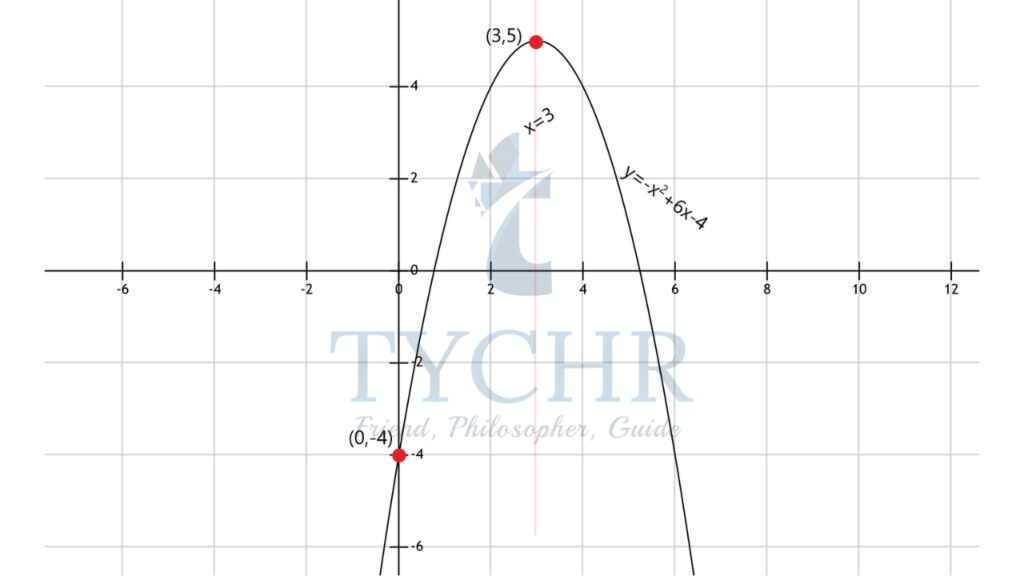
ZEROS OF A QUADRATIC EQUATION
The solution or the root to the equation ax2+bx+c is called the zero of the equation. Graphically, a real zero is the x-coordinate of all the points where f crosses the x-axis.
A quadratic function can have no real zeros, one real zero or two real zeros. It is depicted graphically
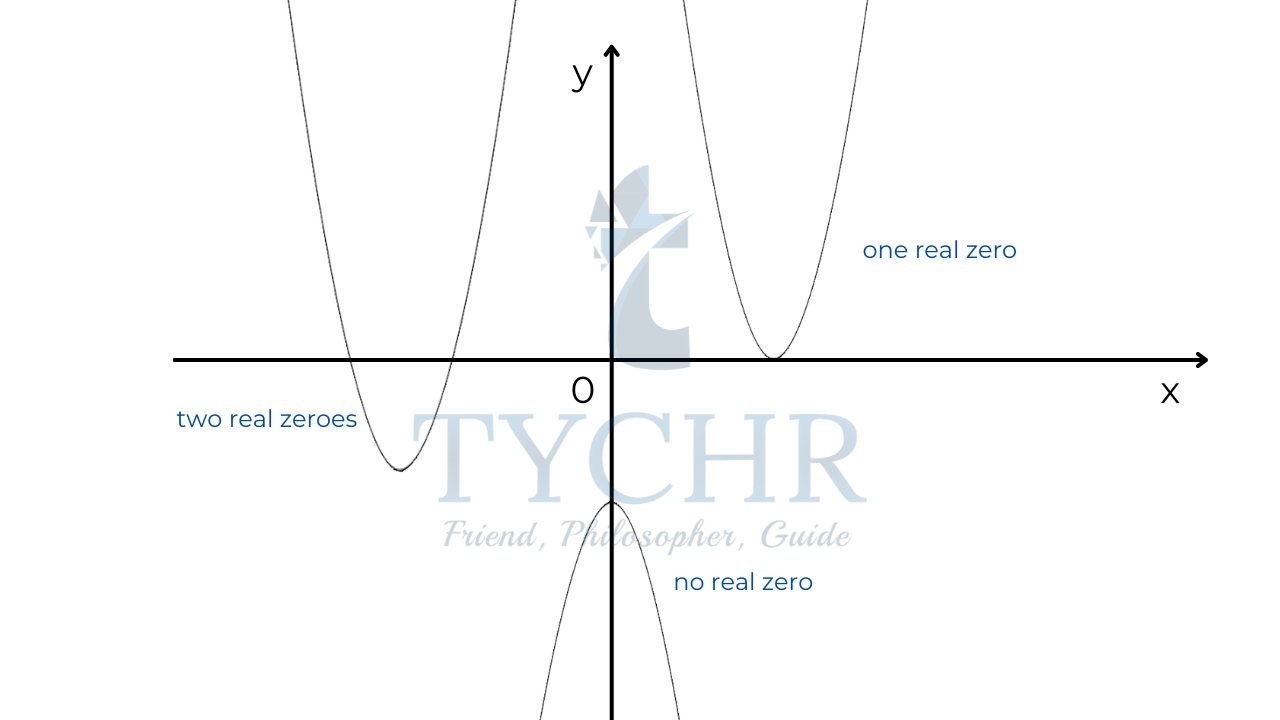
Zeros of a quadratic equation can be evaluated through various methods:
Factorising:
Ex. f(x)=x2+3x-10=0
Splitting the middle term:
xx2+5x-2x-10=0
x(x+5)-2(x+5)=0
(x+5)(x-2)=0
x=-5 or x=2
Therefore, 2 and -5 are the zeros of the given function.
Completeing the Square:
Ex. x2-8x+5=0
Completing the square, as discussed in previous section:
x2-8x+16+5-16=0
(x-4)2 = 11,
x-4=±√11
x=4±√11
Therefore, 4+√11 and 4-√11 are the zeros of the given function.
Graphing:
Graph the given quadratic function using your GDC, and locate the points where the graph crosses the x-axis, the x-coordinate will be the zeros of the function.
Quadratic Formula:
If ax2+bx+c=0, then 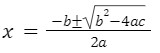 Ex. 2x2+5x-3
Ex. 2x2+5x-3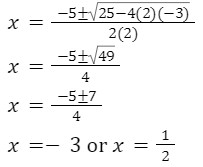 Therefore, -3 and 1/2 are the zeros of the given function.
Therefore, -3 and 1/2 are the zeros of the given function.
THE QUADRATIC FORMULA AND DISCRIMINANT
For the function, ax2+bx+c=0, the zeros can be evaluated using the quadratic formula i.e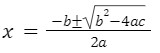
The expression beneath the radical sign b2-4ac, is called the discriminant (denoted by D).
The value of discriminant, gives us details about the nature of the zeros of the given function.
| DISCRIMINANT | NATURE OF ROOTS |
| Positive | Real and distinct |
| Negative | Complex |
| Zero | Real and equal |
| Positive and perfect square | Distinct and rational |
| Positive and not a perfect square | Distinct and irrational |
Ex. For 4x2+4kx+9=0, determine the value(s) of k so that the equation has:
one real zero
two distinct real zeros
no real zeros
For one real zero, the discriminant should be zero:
D=b2-4ac=0
(4k)2 – 4(4)(9) = Q
16k2=16×9
k2=9
k=±3
For two distinct real zeros, the discriminant should be positive:
D>0
b2-4ac>0
(4k)2 -4(4)(9) > 0
k2-9>0
(k-3)(k+3)>0
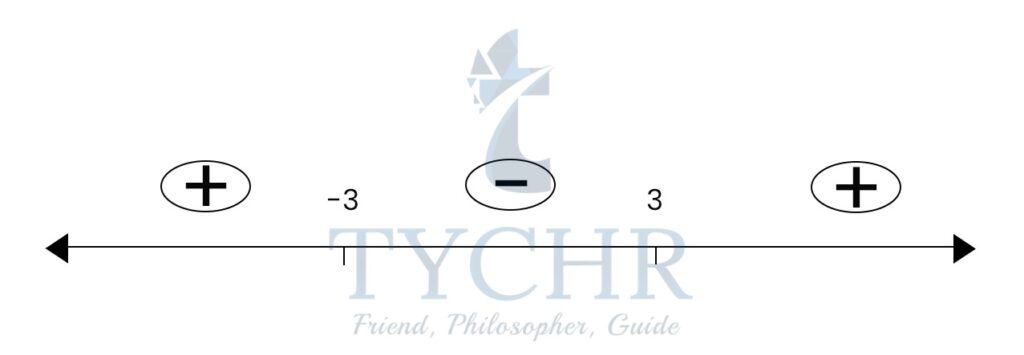
All values of k less than -3 and greater than 3 will make the expression positive. Therefore, the inequality will hold true if k ϵ 𝑘 𝜖 ]−∞, −3[ ∪ ]3, ∞[
For no real zeros, the discriminant should be negative: D<0
From previous part, putting the value of D (k-3)(k+3)<0
From the number line in the previous part, all values of k, between -3 and 3 the expression will be negative.
Therefore, the inequality will hold true if 𝑘 𝜖 ]−3,3[
THE GRAPH OF f(x)=a(x-p)(x-q) (FACTORISED FORM)
If f(x)=a(x-p)(x-q), then the quadratic function intersects the x-axis at the points (p,0) and (q,0).
The general form ax^2+bx+c can be converted to f(x)=a(x-p)(x-q), by simple factorisation, hence the name (factorised form).
As parabola is always symmetric, the x-intercepts, (p,0) and (q,0) are equidistant from axis of symmetry. So we can find the axis of symmetry and x-coordinate of the vertex by taking the average of p and q.
Ex. Find the equation of the axis of symmetry and the coordinates of the x-intercepts, the y-intercepts and the vertex. Also sketch the graph
f(x)=(x-4)(x-2)
Clearly, the parabola is concave up, as the coefficient of x2 is positive, which also implies that the vertex will be a minimum point.
From the given equation p=4 and q=2.
So, the x-intercepts are: (4,0) and (2,0)
Now, taking the average of p and (p + q)/2 = (4+2)/2 = 3
Therefore, the axis of symmetry is x=3.
Now, at x=3, f(x)=(3-4)(3-2)=-1
So, the vertex is at (3,-1)
The y-intercept will be at x=0,
y=(0-4)(0-2)
y=8
So, the y-intercept is at (0,8)
Using the above information, to sketch the graph of f(x):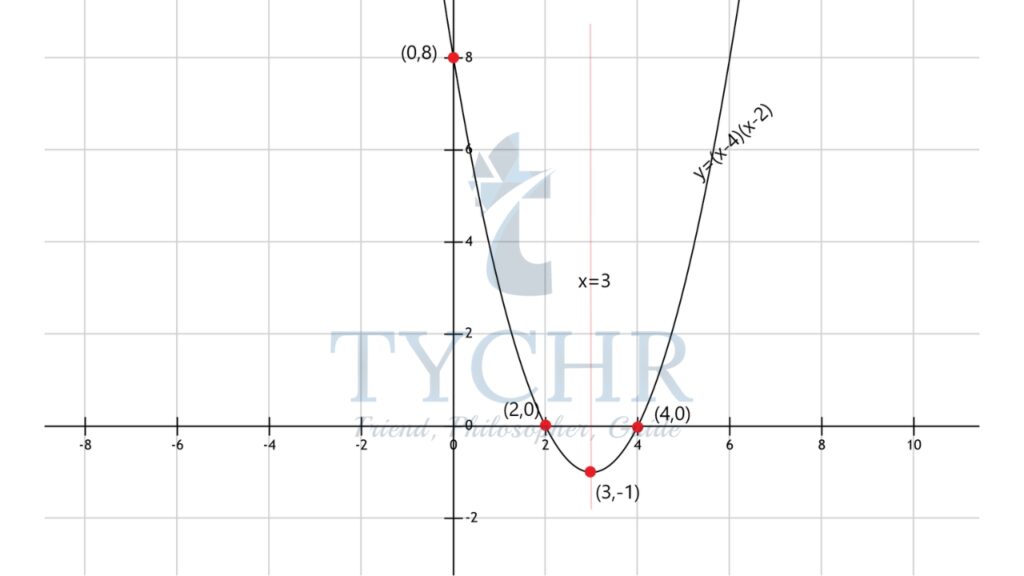
RATIONAL FUNCTIONS
RECIPROCAL FUNCTION
The reciprocal of a number is 1 divided by that number.
A reciprocal function is f(x) = k/x, where k is a non-zero constant.
Ex. f(x) = 1/x , the graph is shown below: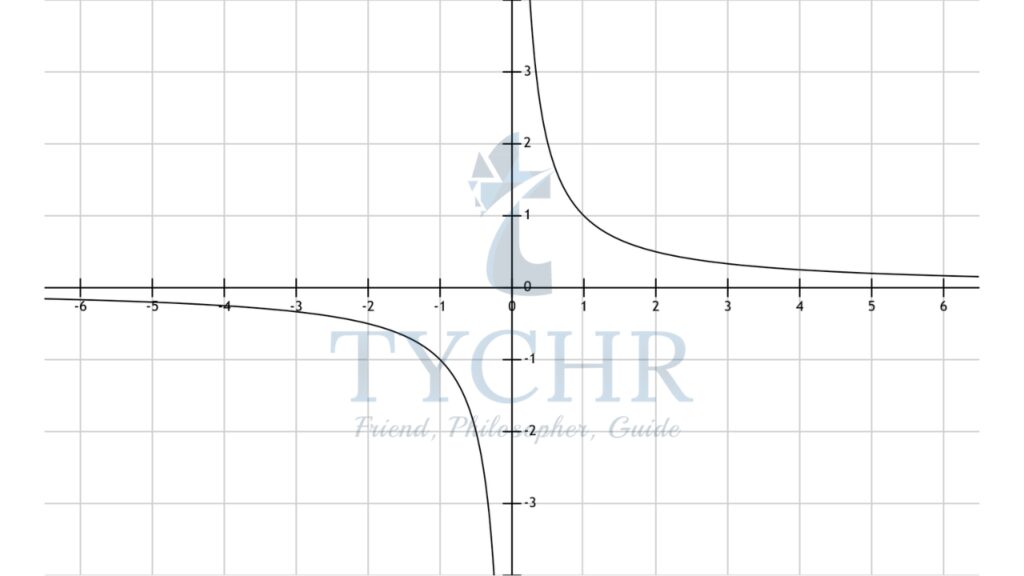
The domain of f(x) is x ϵ R-{0}
This means x can be any real number, other than zero.
The range of f(x) is y ϵ R-{0}
This means y can be any real number, other than zero.
The domain and range of f(x) are evident from the graph. It can be clearly seen that x=0 and y=0 are asymptotes.
(Asymptote- a straight line that continually approaches a given curve but does not meet it at any finite distance)
The line y=0 (as an horizontal asymptote), indicates that f(x) tend towards, but never reaches zero, as x gets very large (or tends to infinity).
The line x=0 (as an vertical asymptote), indicates that f(x) tend towards, but never reaches infinity, as x gets very close to zero.
RATIONAL FUNCTIONS
Functions of the form R(x) = f(x)/g(x), where f and g are polynomials are called rational functions. The domain of the function R is the set of all real numbers not including the real zeros of the polynomial g in the denominator.
We will consider f and g to be linear polynomials.
Examples of rational functions-
p(x) = 4/(x-6) , q(x) = 4/(x-6)
The domain of function p is x ϵ R-{6}
The domain of functon q is x ϵ R-{9/5}
Ex. Sketch y = 1/(x-2). Show the asymptotes, write the equation of the horizontal and vertical asymptotes and state the domain and range.
y = 1/(x-2) is a horizontal translation of y = 1/x by two units to the right: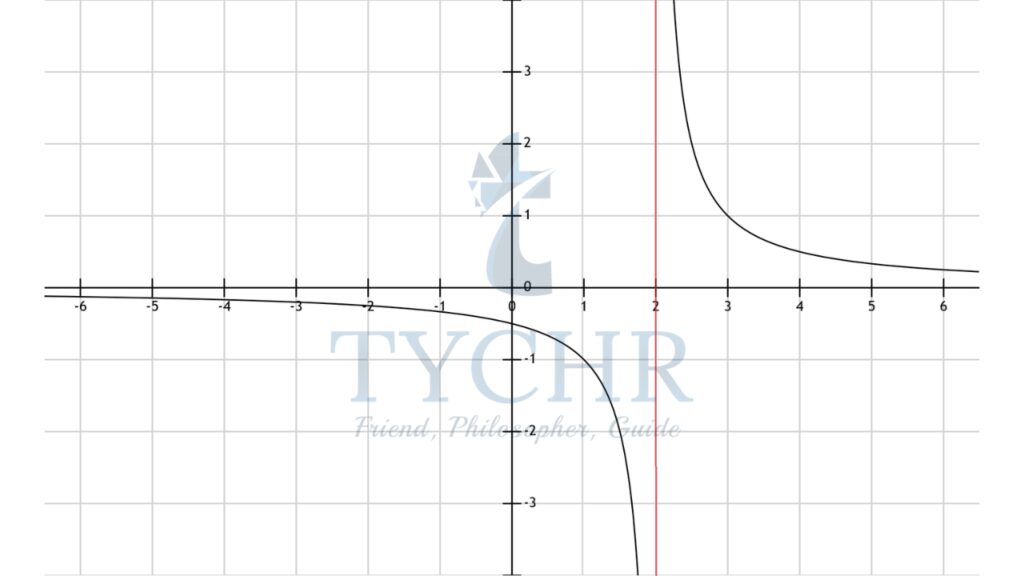
From the equation and the graph, the function tends to infinity at x=2, therefore, x=2 is the vertical asymptote.
Again from the equation and graph, the function tends to zero at y=0, therefore y=0 is the horizontal asymptote.
The domain of f(x) is x ϵ R-{2}
The range of f(x) is y ϵ R-{0}
Ex. Consider the function y = (4x + 1)/(2x-6) Sketch the graph, show asymptotes and find domain and range. y = (4x+1)/(2x-6). We know that, we get a vertical asymptote when the denominator is zero:
2x-6=0, i.e. x=3, Therefore, x=3 is a vertical asymptote.
For horizontal asymptote, we first write x in terms of y:
y(2x-6)=4x+1
2xy-6y=4x+1
2xy-4x=6y+1
x(2y-4)=6y+1
x = (6y + 1)/(2y-4)
There will be a horizontal asymptote when the denominator of the above expression will be zero:
2y-4=0
y=2
Therefore, y=2 is the horizontal asymptote.
Now finding x and y-intercepts:
For y-intercept, putting x=0 in equation 2: y = ((4(0) + 1)/(2(0)-6)y
y = -(1/6)
Therefore, (0, -(1/6))is the y-intercept.
For x-intercept, putting y=0 in equation : x = ((6(0)+1)/2(0)-4)x
x= -(1/x) Therefore,(-1/4 , 0) is the x-intercept.
Now sketching the graph: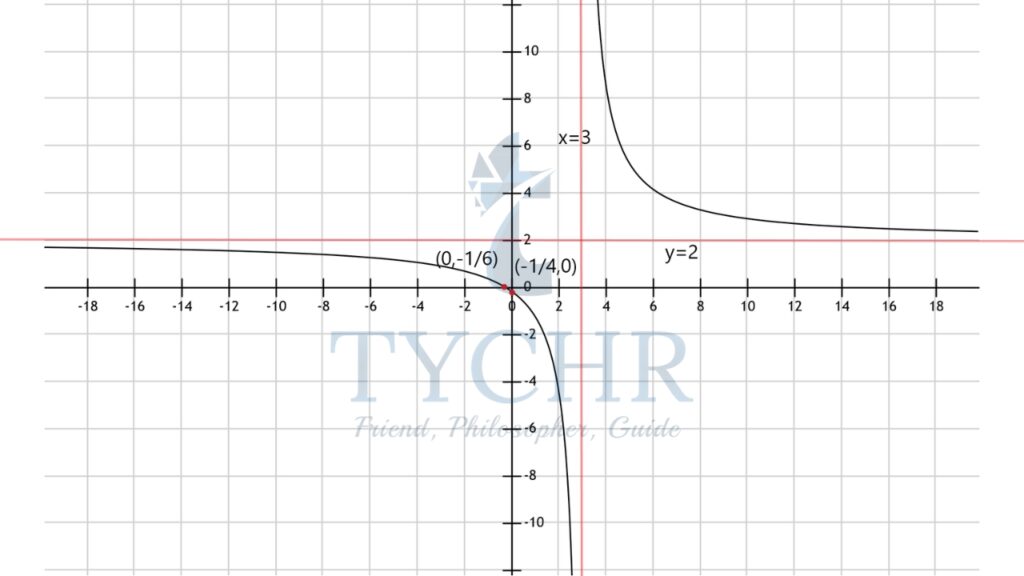
From the graph and the equations ① and ②:
Domain- x ϵ R-{3}
Range- y ϵ R-{2}
SOLVING EQUATIONS AND INEQUALITIES
EQUATIONS INVOLVING A RADICAL
To solve equations involving radicals, take the radical term to one side, and the left over terms to another and then raise it to a power which removes the radical. You will be left with a polynomial, which we know how to solve.
Ex. Solve √(3𝑥 + 6) = 2𝑥 + 1
Squaring both sides:
3𝑥 + 6 = (2𝑥 + 1)2
3x+6=4x2+4x+1
4x2+x-5=0
Factorising:
4x2-4x+5x-5=0
4x(x-1)+5(x-1)=0
(x-1)(4x+5)=0
x=1 or x = -(5/4)
When we put x=1 in the original equation, we get LHS=RHS, but when we put x = -(5/4)x, it does not satisfy the equation.
This x = -(5/4) is called an extraneous solution. This happened because we squared the original equation to solve it. So, whenever we raise any equation to a power to solve it, we are supposed to check all the solutions in the original equation.
EQUATIONS INVOLVING FRACTIONS
To solve equations involving fractions, we have to take LCM (Least common multiple) of all the fractions, and make their denominators equal to the LCM.
Ex. (2x/(4-x2)) +( 1/(x-2)) = 3
(2x+/((2-x)(2+x)) + (1/(x+2)) = 3
The least common multiple here is (2-x)(2+x):![]() 2+x=3(2-x)(2+x)
2+x=3(2-x)(2+x)
2+x=12-3x2
3x2+x-10=0
Factorising:
(3x-5)(x+2)=0
x = 5/3 or x=-2
x=-2 cannot be a solution, because it will cause division by zero in the original equation.
Therefore, x = 5/3 is the only solution.
EQUATIONS IN QUADRATIC FORM
In previous sections we have learnt how to solve quadratic equations, now we will se how we can use that method to solve other type of equations:
Ex. 2m4-5m2+2=0
Putting m2=t
2t2-5t+2=0
Factorising:
(2t-1)(t-2)=0
t=1/2 or t=2
Now t=m2, so:
m2=1/2 or m2=2![]() All four values satisfy the original equation, therefore the solutions to the equation are:
All four values satisfy the original equation, therefore the solutions to the equation are: ![]() Similarly, if the given equation has fractional powers, it can be converted to a quadratic by a simple substitution:
Similarly, if the given equation has fractional powers, it can be converted to a quadratic by a simple substitution:
Ex. w1/2 = 4w1/4 – 2
Putting w1/4 = t
The equation becomes:
t2-4t+2=0
Using quadratic formula: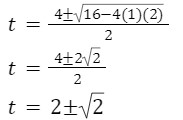 Replacing t by w1/4
Replacing t by w1/4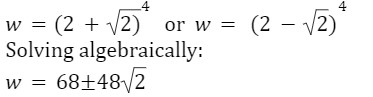
EQUATIONS INVOLVING ABSOLUTE VALUE (MODULUS)
Meaning of Modulus
Modulus of any number x denoted by |x| is given by:
|x|=x if x≥0
=-x if x<0
|x| geometrically is the distance between the coordinate x and the origin on the number line.
More generally:
|x-a| is the distance between the coordinates of x and a on the number line.
An equation involving absolute value can be solved in two ways, one is by definition and the other by squaring both sides.
Ex. |2x-3|=|7-3x|
Solving by definition:
2x-3=-(7-3x) or 2x-3=7-3x
2x-3=-7+3x or 5x=10
x=4 or x=2
Solving by squaring:
(2x – 3)2 = (7 – 3x)2
4x2-12x+9=49-42x+9x2
5x2-30x+40=0
xx2-6x+8=0
Factorsing:
(x-2)(x-4)=0
x=2 or x=4
Checking Graphically:
Plotting the graphs of y=|2x-3| and y=|7-3x| and checking the x-coordinates of the intersection points: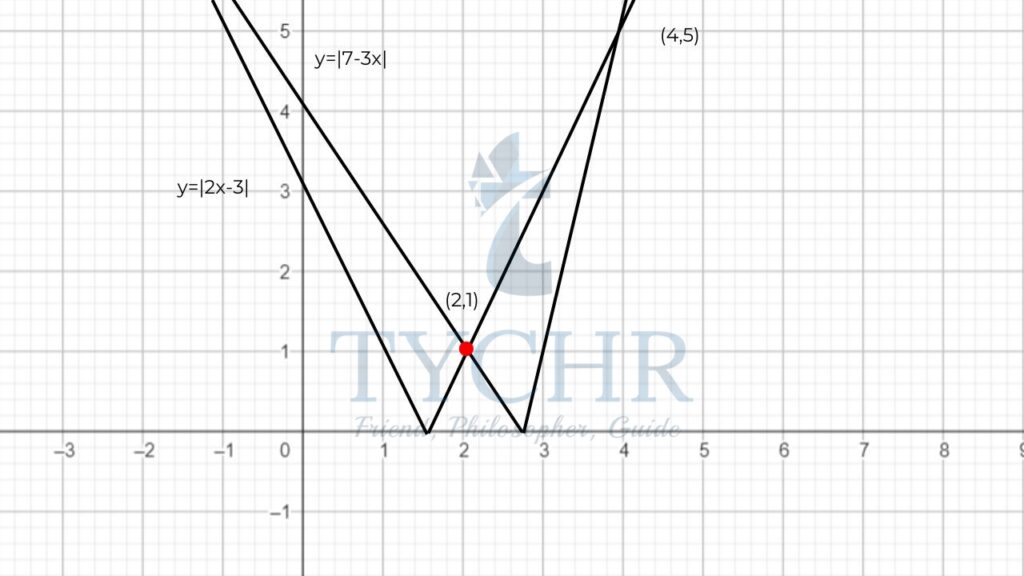
QUADRATIC INEQUALITIES
Ex. x2+4x-45>0
Factorise:
(x-5)(x+9)>0
Now, plot the solutions of the expresision in the inequality on the number line.
When we plot 5 and -9 on the number line, we get three intervals. We need to take a number from each interval, put it in the expression and check whether the expression becomes positive or negative.
The sign of the expression for each has been marked on the number line.
We need our expression to be positive, so we take the values of x greater than 5 or less than -9.
Therefore, the inequality will hold if 𝑥 𝜖 ]−∞, −9[ ∪ ]5, ∞[
Note that we have not included -9 and 5 because they will make the expression zero.

