Sign Up for Your Free Trial Class Today!
Dive in, explore, and experience firsthand what sets us apart.

By the end of this chapter, you will be familiar with:
By now we are familiar with differentiating common functions.
In this unit we carry out the process of differentiation in reverse. That is, we start with a given function, f(x) say, and ask what function or functions, F(x), would have f(x) as their derivative. This leads us to the concepts of an antiderivative and integration.
Consider the function f(x)=3x2+7x-2. Suppose we write its derivative as f(x), that is ![]() . We already know how to find this derivative by differentiating tem by term to obtain
. We already know how to find this derivative by differentiating tem by term to obtain ![]() Suppose now that we work back to front and ask ourselves which function or functions could possibly have 6x+7 as a derivative. Clearly, one answer to this question is the function 3x2+7x-2. We say f(x)=3x2+7x-2 is an antiderivative of f(x)=6x+7.
Suppose now that we work back to front and ask ourselves which function or functions could possibly have 6x+7 as a derivative. Clearly, one answer to this question is the function 3x2+7x-2. We say f(x)=3x2+7x-2 is an antiderivative of f(x)=6x+7.
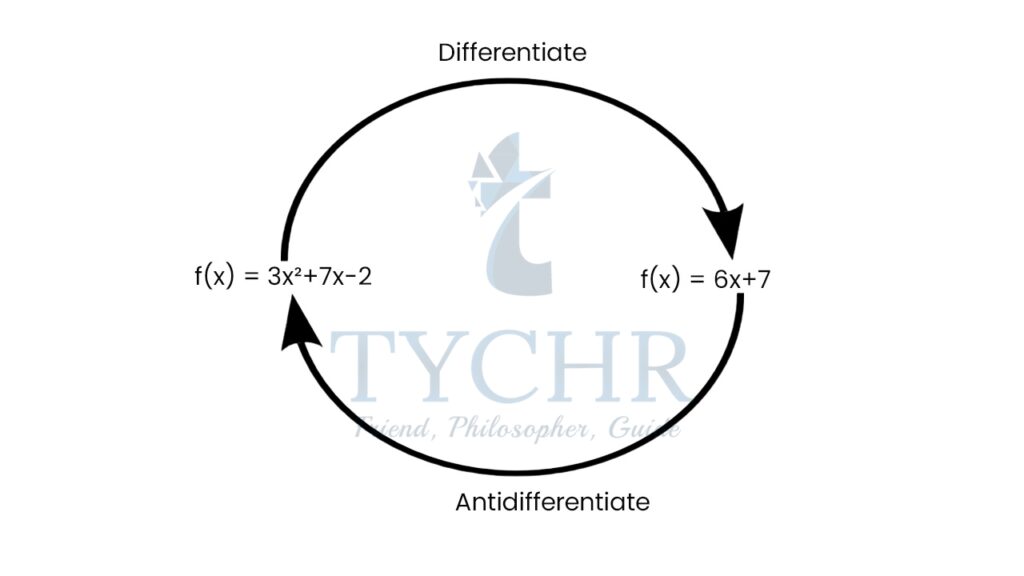
There are however other functions which have derivative 6x+7. Example
3x2+7x+3
3x2+7x
3x2+7x-12
The reason why all of these functions have the same derivative is that the constant term disappears during differentiation. So, all of these are antiderivatives of 6x+7.
Given any antiderivative of f(x), all others can be obtained by simply adding a different constant. In other words, if F(x) is an antiderivative of f(x), then so too is f(x)+C for any constant C.
If f'(x)=f(x) we write f(x)dx=f(x)+C
The expression ∫f(x)dx is called an indefinite integral.
Table of some common indefinite integrals:
f(x) | ∫f(x)dx=f(x)+C |
k (constant) | kx+C |
xn |
|
sin x | –cos x +C |
cos x | sin x +C |
ex | ex+C |
| ln x +C |
Rules for integration:
Ex. Find indefinite integrals of the following:
Solution:
Integration by Substitution (also called “u-Substitution” or “The Reverse Chain Rule”) is a method to find an integral, but only when it can be set up in a special way.
Ex. ![]() We know that
We know that![]()
But here, we have another function inside the sine function.
Recall that, in chain rule of differentiation, we differentiate the inner function after differentiating the outer.
Let us multiply and divide the differentiation of the inner function in the intergral.![]() Now, we will put 3x+2=u
Now, we will put 3x+2=u
Differentiate the above equation:
3dx=du
Substitue the value of 3x+2 and 3dx in the integral![]()
Now, we can easily integrate-![]()
Putting the value of u:![]()
Using this simple substitution method, we have the following results:
f(x) | ∫f(x) |
(ax+b)n |
|
eax+b |
|
|
|
Ex. ![]() Let u=5x3+2
Let u=5x3+2
hence, du=15x2dx
We will need a factor of 15 in the integral![]() Substituting the value of u and du:
Substituting the value of u and du:![]() Now we can simply integrate:
Now we can simply integrate:![]() Substituing the value of u:
Substituing the value of u:![]()
Ex. ![]() Let sin(2x2)=u
Let sin(2x2)=u
hence, cos (2x2) 4xdx=du
We will need a factor of 4 in the integral![]() Substituting the value of u and du:
Substituting the value of u and du:![]() Now we can simply integrate:
Now we can simply integrate:![]()
![]() Substituing the value of u:
Substituing the value of u:![]()
Consider that portion of the graph of y=f(x).

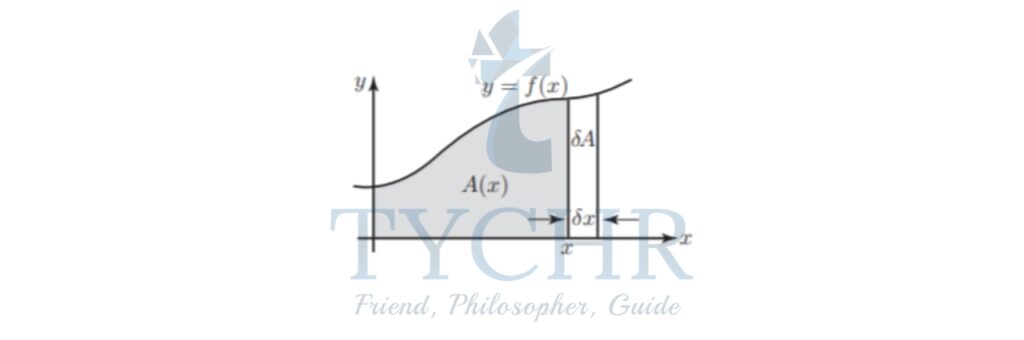
We can use the previous section to interpret this result.
Given that f(x) is the derivative of A(x) then, A(x) must be an antiderivative of f(x), i.e.
Ax=f(x)+C ①
We wrote f(x)+C for a whole family of functions all of which are antiderivatives when F(x) is. Now, we are looking for a specific antiderivative by choosing a specific value for
We can use this result as follows:
Given a function f(x), then the formula in Equation ① can tell us the area under the graph provided we can calculate an antiderivative F(x).
Suppose now we want to find the area under the graph between x=a and x=b as shown below:
The total area up to x=b is given, using Equation ①, by
A(b)=F(b)+C
The total area up to x=a is given, using Equation ①, by
A(a)=F(a)+C
And so, subtracting, the area between a and b is
A(b)-A(a)=F(b)-F(a)
Note how the C’s cancel out.
This area can be denoted by:![]()
This is what we call definite integral.
Properties of definite integral:
The fundamental theorem of calculus is a theorem that links the concept of differentiating a function with the concept of integrating a function.
The theorem has two versions:
Ex. Calculate the area under the curve ![]() in the domain x=1 to x=2.
in the domain x=1 to x=2.
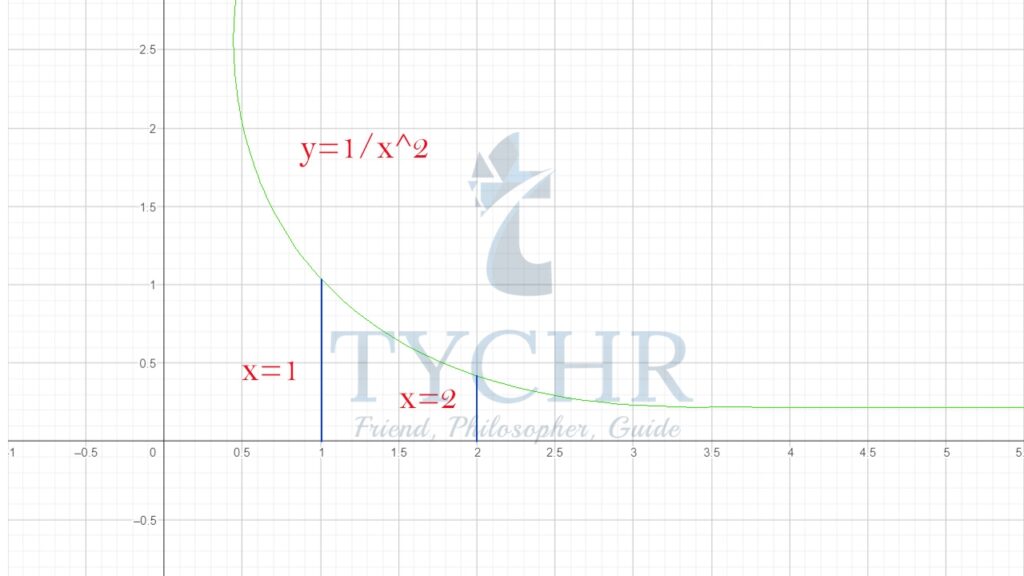
![]() Now,
Now, ![]() A=F2-F(1)
A=F2-F(1)
A=-12-(-1) ![]() units
units
Ex. Evaluate ![]() Using fundamental theorem of calculus:
Using fundamental theorem of calculus:![]()
Ex. Evaluate ![]()
![]()
![]()
![]()
![]()
![]()
Evaluating definite integrals by substitution:
Ex. Evaluate ![]() Putting 3x-2=u
Putting 3x-2=u
3dx=du
Since we are changing the variable, the limits will also change.
We have 3x-2=u
At x=2, u=4
At x=3, u=7
Now, the limits will become from u=4 to u=7 Putting the limits, u and du in the integral:![]()
![]()
![]()
![]()
Recall that the area under the graph of y=f(x) between x=a and x=b, is given by:![]() Here, F(x) is the antiderivative of f(x)
Here, F(x) is the antiderivative of f(x)
If f(x) and g(x) are two functions, given that f(x)>g(x) in the interval [a,b], then the area between the curves y=f(x) and y=g(x) in this intevral is given by-![]() In terms of antiderivatives:
In terms of antiderivatives: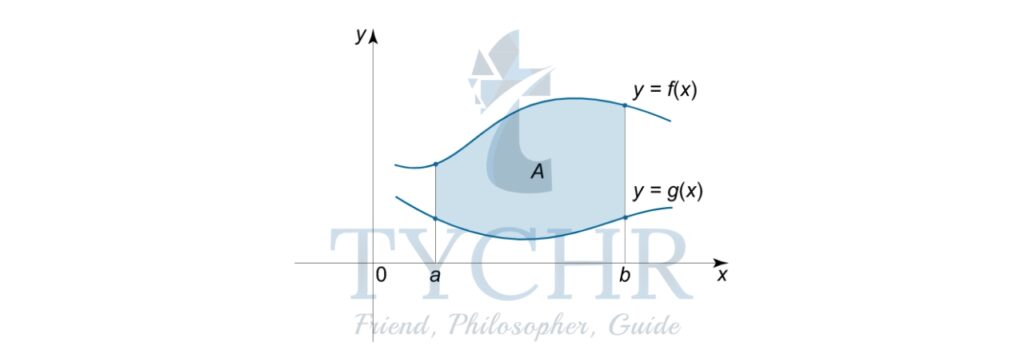
![]() Here, F(x) and G(x) are antiderivatives of the functions f(x) and g(x) respectively.
Here, F(x) and G(x) are antiderivatives of the functions f(x) and g(x) respectively.
Ex. Determine the area of the region enclosed by y=x2 and ![]()
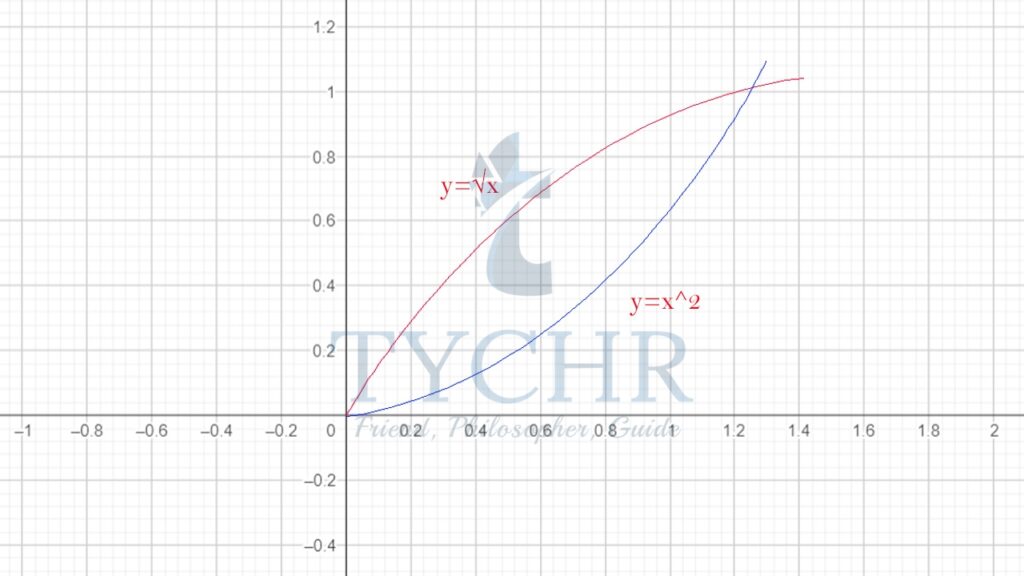
First lets plot the graph of the two functions.
The intersection of the two graphs is at 0,0 and (1,1)
The limits of the integration will be x=0 and x=1.![]()
![]()
![]()
![]() unit
unit
Ex. Find the area of the region in the first quadrant enclosed by the graphs of y2=x and y=x-2
Consider the graph:
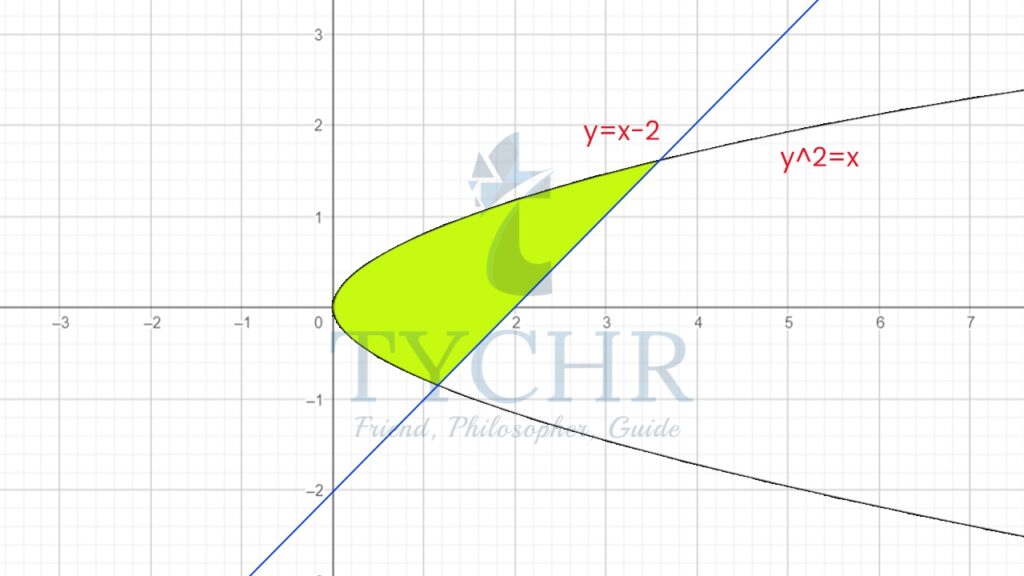
The graphs here, are along y-axis, so we will write the expressions, in terms of y:
x=y2
x=y+2
Now, we will determine the intersection of the two curves-
y2=y+2
(y+1)(y-2)=0
y=-1, y=2
Area =![]()
![]()
![]()
![]()
![]() units
units
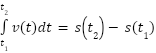 is the displacement from t1 to t2.
is the displacement from t1 to t2.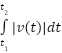 t gives the total distance travelled from t1 to t2.
t gives the total distance travelled from t1 to t2.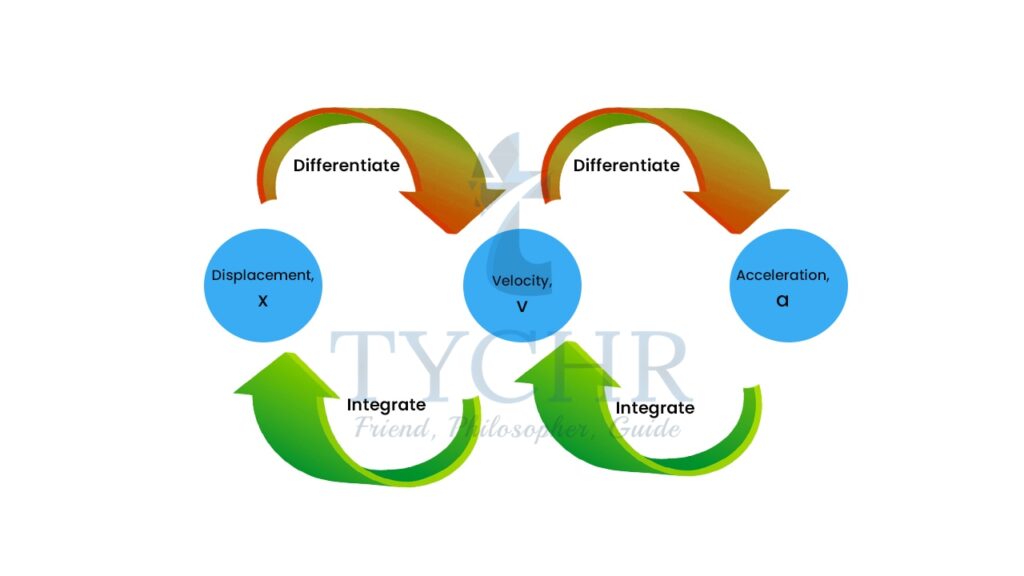
Ex. A particle P is moving along a straight line. The acceleration ams-1 from O can be written as a function of t
a=t+19
Suppose we know that when t=0, we have s=0 and when t=4 we have s=10. Find the displacement when t=10.
First we will find velocity by integrating the acceleration function:![]()
![]()
![]()
Now, we will integrate velocity to obtain the displacement:![]()
![]()
![]()
Now, putting t=0 and s=0
0=0+0+0+C2
C2=0
The displacement now becomes-![]()
Putting t=4 and s=10![]()
![]()
The displacement now becomes-![]()
Putting t=10
s=735 units
Dive in, explore, and experience firsthand what sets us apart.

Download our Successful College Application Guide developed by counselors from the University of Cambridge for institutions like Oxbridge alongside other Ivy Leagues. To join our college counseling program, call at +918825012255
We are hiring a Business Development Associate and Content Writer and Social Media Strategist at our organisation TYCHR to take over the responsibility of conducting workshops and excelling in new sales territory. View More