Trigonometric Functions and Equations Notes
By the end of this chapter, you should be familiar with:
- The radian measure of angles
- Finding the length of an arc and area of a sector
- The unit circle and definitions of sinθ,cosθ and tanθ
- The exact value of some trigonometric ratios
- Identities of trigonometric ratios
- Graphs of sinθ, cosθ and tanθ
- Composite functions of trigonometric ratios and their graphs.
- Transformation of the graphs of trigonometric functions
- Solving trigonometric equations.
RADIAN MEASURE, ARCS, SECTORS AND SEGMENTS
RADIAN MEASURE
We already know how to use degrees when measuring angles, but most science and engineering applications use radians. Radians are an alternative way of measuring the size of an angle.
A radian is the meausre of the angle with its vertex at the centre of the circle and two radii with their end points on the circumference and these two points are 1 radii apart.
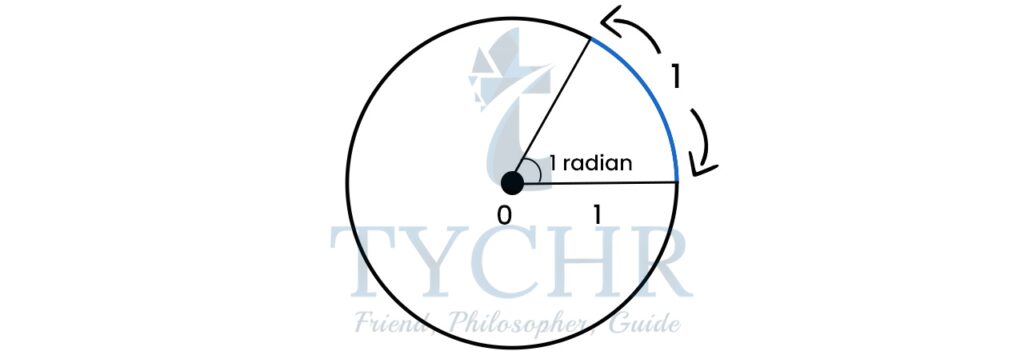
Note that, the circumference of a circle is 2𝜋𝑟 which means there are 2𝜋 radians in a circle. We also know that a full circle has 360°
Therefore, 2𝜋 radians = 360° which means radians = 180°
Conversion between radians and degrees: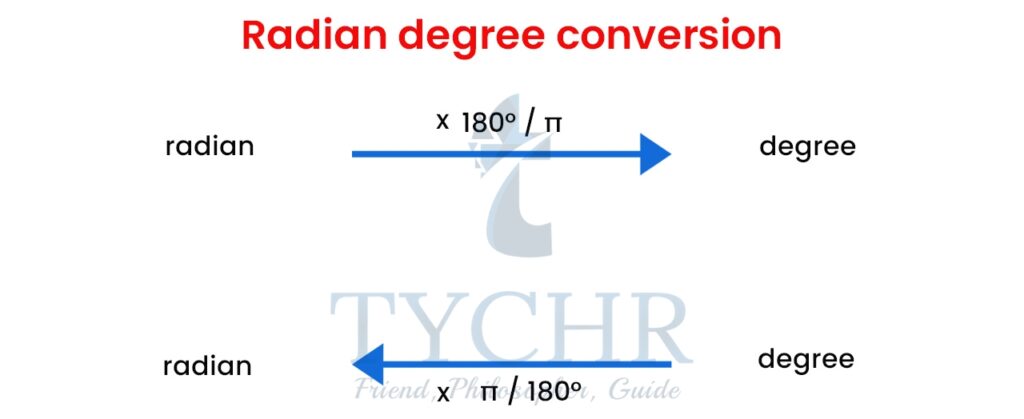
Ex. Convert 30° into radians.
30° = 30π/180 radians = π/6 radians
Ex. Convert π/6 into degrees.
π/6 radians = (π/6) + (180 π) degrees = 30°
Degree measure and radian measure for common angles: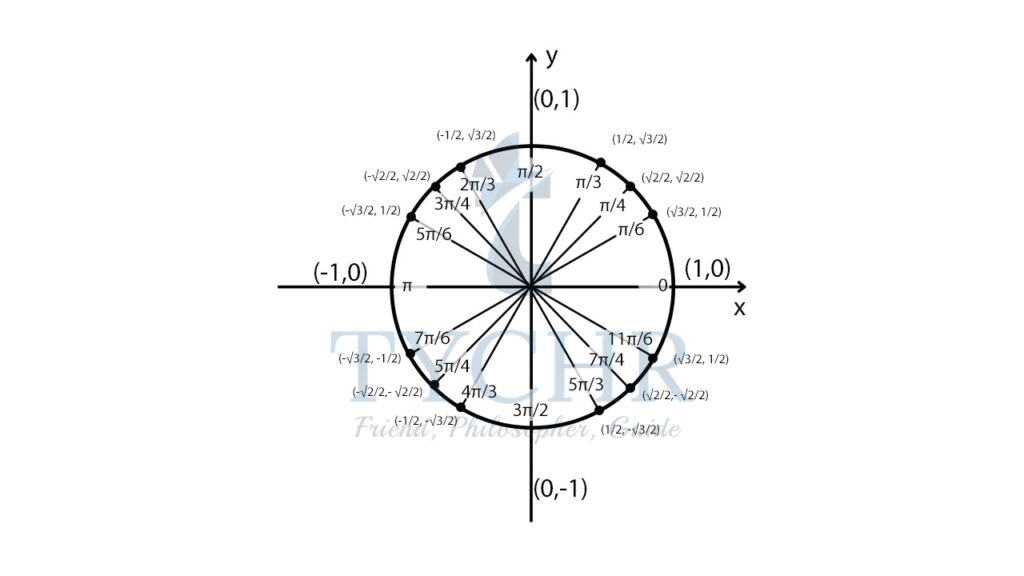
ARC LENGTH
For a circle of radius 𝒓 , a central angle 𝜽 subtends an arc of the circle of length s given by , where 𝒔 = 𝒓𝜽, where 𝜃 is measured in radians.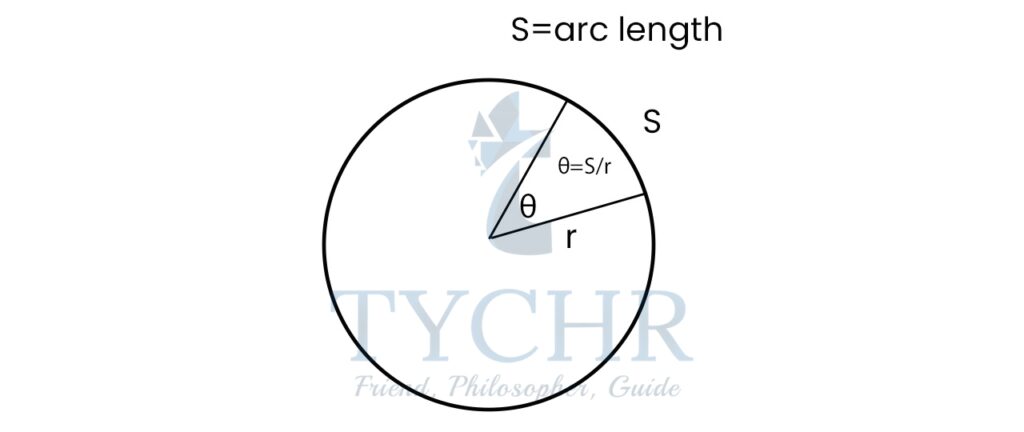
If the angle is in degrees, then we use s = 2πr(𝜽/360)
Ex. A circle has a radius of 10 centimeters. Find the length of the arc of the circle subtended by a central angle of 150°.
s = 2πr(𝜽/360)
s = 2π(10)(150/360)
s = 25π/3
s = 26.18s
SECTOR AND SEGMENT OF A CIRCLE
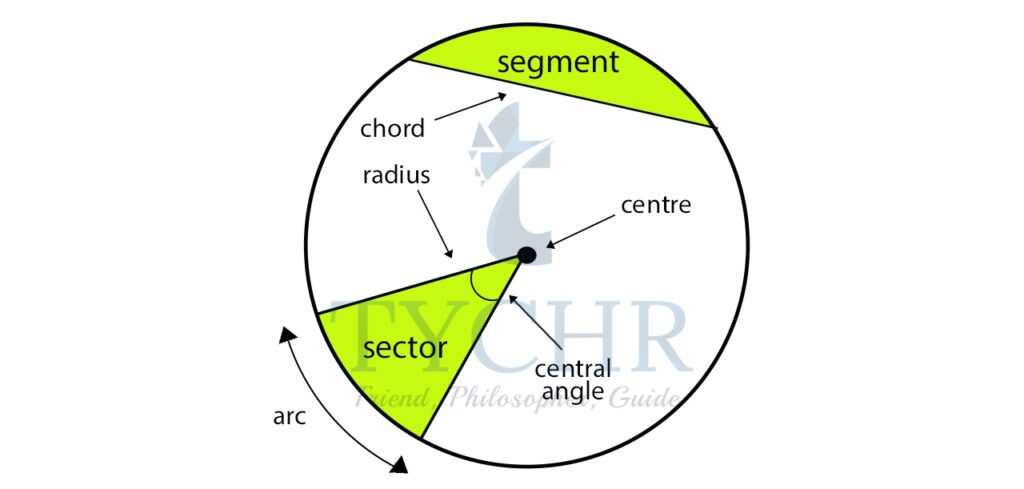
- A sector is the region enclosed by two radii and an arc.
- A chord is the line segment joining two points on the circumference of a circle.
- A segment is the region between a chord and an arc.
We know that the length of an arc of a circle is given by 𝒔 = 𝒓𝜽
The area of of sector will be A = (πr2/2πr)(r𝜽)
A = (1/2)r2𝜽
TRIGONOMETRIC RATIOS IN THE UNIT CIRCLE
We consider a circle with centre at , radius of one unit and equation .
Now, Angles in standard position in the unit circle are measured starting on the positive -axis and turning anticlockwise (positive angles) or clockwise (negative angles).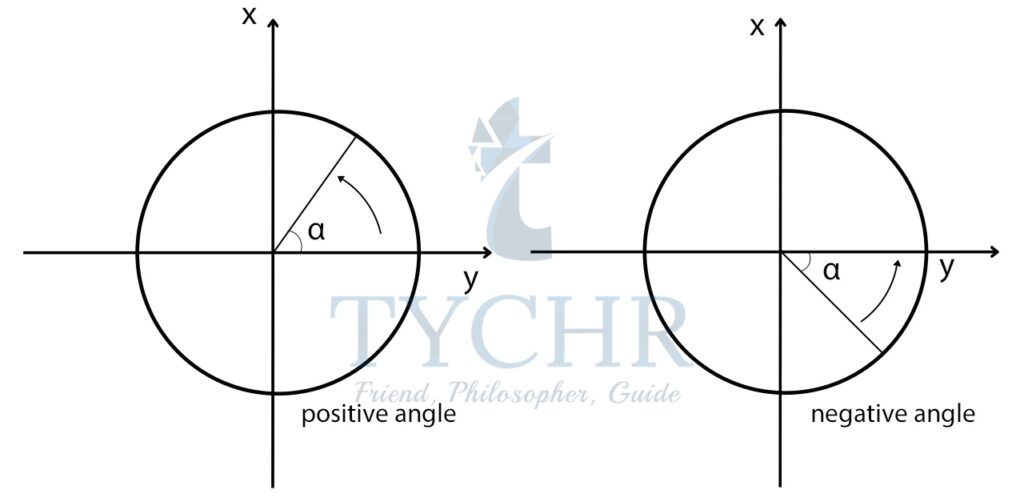
Now, the coordinate axis divides the plane into four quadrants, first, second, third and fourth.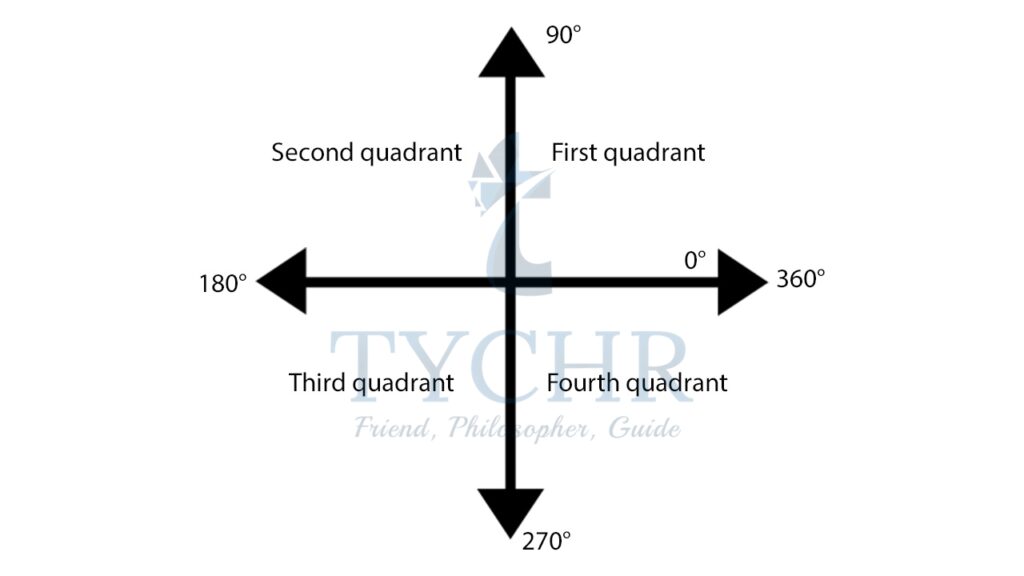
The and -coordinates of the unit circle are used to define the trigonometric ratios sine, cosine and tangent. (sin, cos, tan).
The -coordinate is assigned to the sin function -coordinate is assigned to the cosine function and the ratio of the two coordinates y/x is assigned to the tangent function. tan𝜽 =(sin𝜽/cos𝜽)
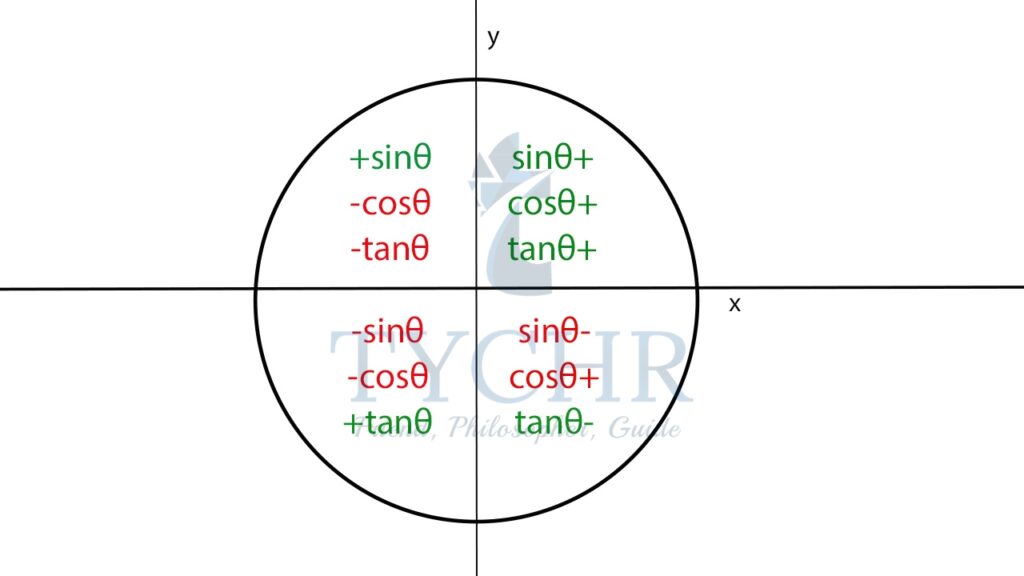
Now, the signs of the trigonometric ratios in each quadrant is defined as:
The standard position of an angle is the position of an angle with its vertex at the origin of a unit circle and one side fixed on the positive -axis. This side is called the initial side of the angle. The other side of the angle, called the terminal side, will intersect the circle at a point.
- Angles with terminal sides that intersect the circle at points with with the same value have equal sines
- Angles with terminal sides that intersect the circle at points with the same value have equal cosines.
- Angles with terminal sides that are directly opposite each other on a line drawn through the origin have the same tangents.
- Angles can be easily interchanges, by considering the and -coordinates.
Keeping this idea in mind, the following formulas are derived:
We don’t need to memorise the formulas, just understand them with intuition and generate them when required.
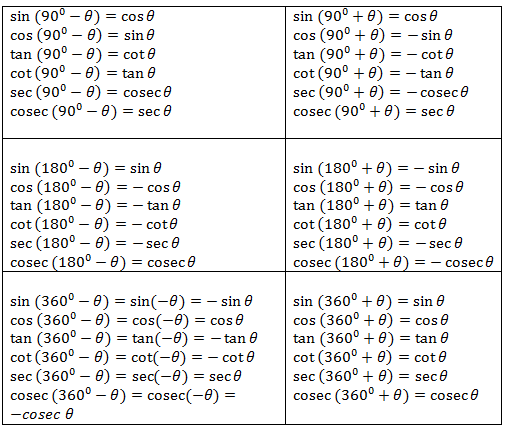
Ex. Evaluate the three trigonometric functions for arc length l = 3π/2
An arc length of l = 3π/2 is equivalent to three-quarters of the cricumference of the unit circle, so it terminates at the point(0,-1) . By definition: sin(3π/2) = y = -1 , cos(3π/2) = x = 0 , sin(3π/2) = y/x = -1/0 is undefined.
Ex. Find another angle less 360° than that has the same cosine as 50°.
Now, some common values of trigonometric ratios to memorise:
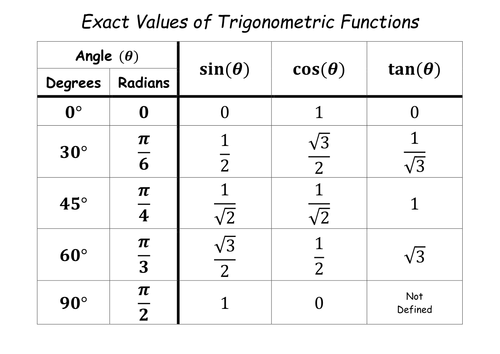
Using these values, most of the trigonometric ratios can be evaluated without using GDC.
GRAPH OF TRIGONOMETRIC FUNCTIONS
SINE CURVE
𝑦 = sin x
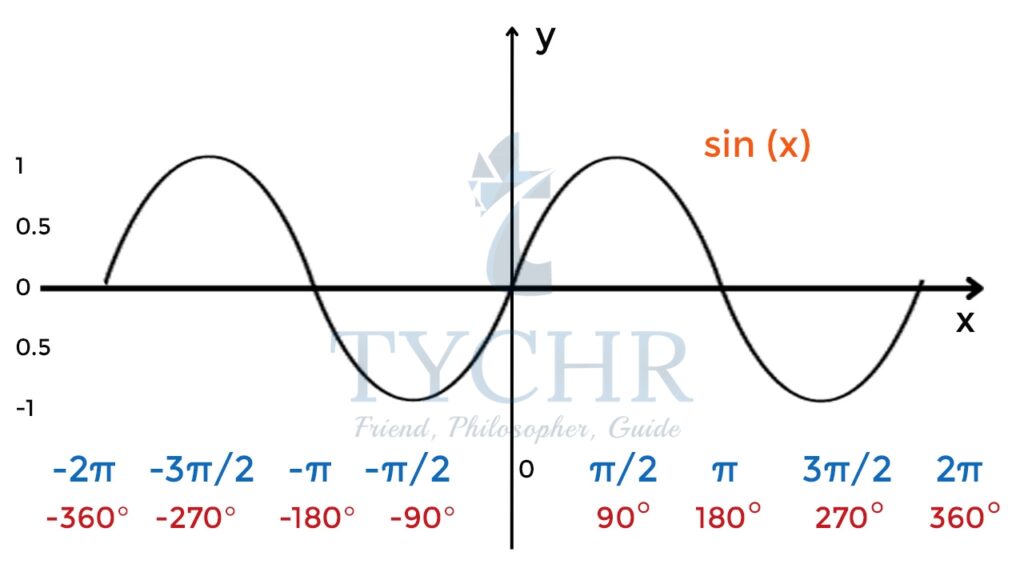
- Maximum value is 1
- Minimum value is -1
- Periodic function with period- 2𝜋
- Completes 1 wavelength in 2𝜋 radians
- Amplitude – (Difference between maximum and minimum values divided by 2)
COSINE CURVE
y=cosx
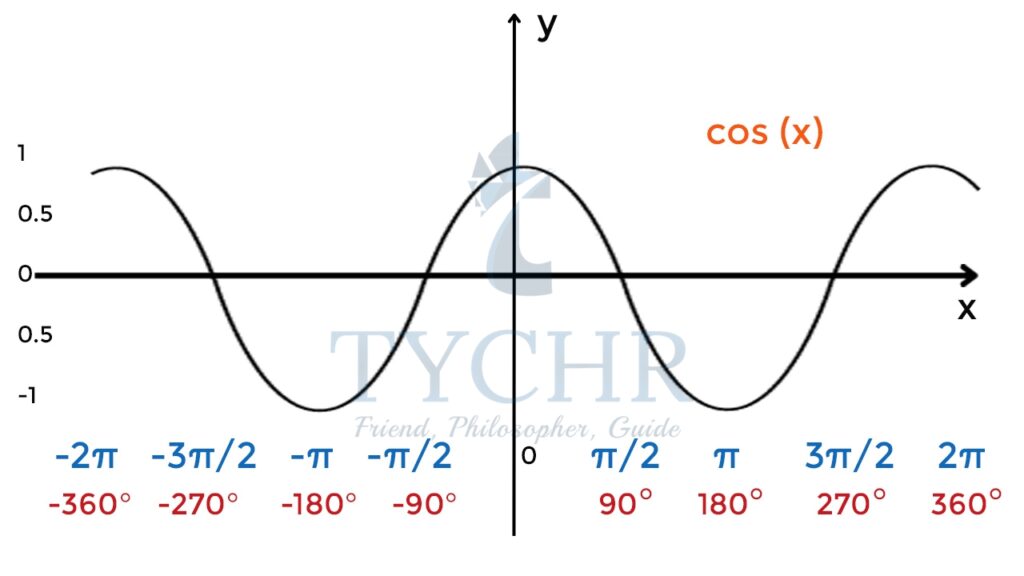
Cosine curve is obtained by shifting the sine curve horizontally left by π/2 units. All properties of cosine curve is same as that of the sine curve.
TANGENT CURVE
y = tanx
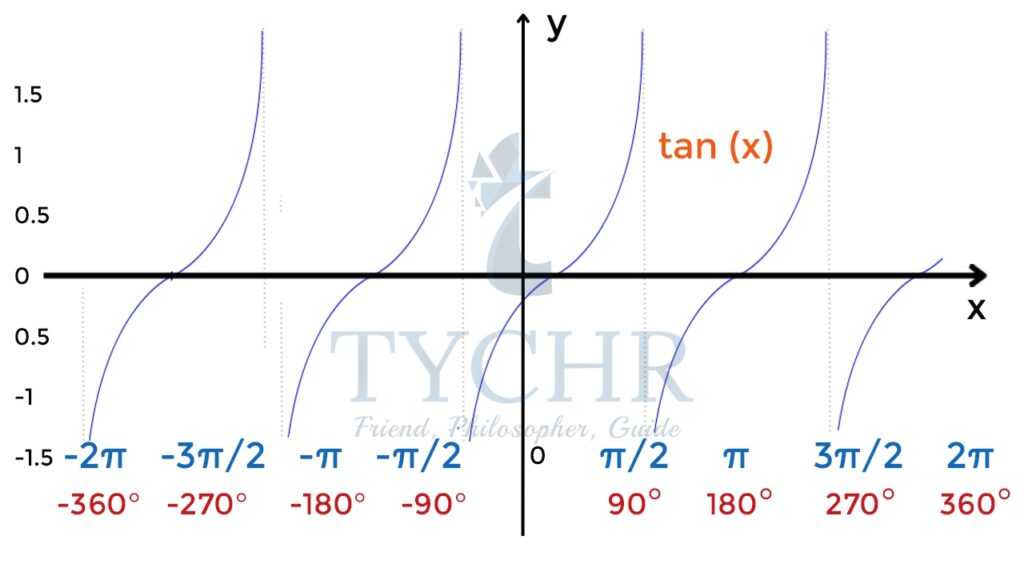
- Periodic function with period –𝜋
- No extrema points
TRANSFORMATION OF TRIGONOMETRIC GRAPHS
We have already dicsussed transformation of graphs in previous chapters. Let’s take a brief review:
Function notation | Type of transformation |
𝑓(𝑥) + 𝑑 | Vertical translation up units |
𝑓(𝑥) – 𝑑 | Vertical translation down units |
𝑓(𝑥 + c) | Horizontal translation left units |
𝑓(𝑥 – c) | Horizontal translation right units |
-𝑓(𝑥) | Reflection over -axis |
𝑓(-𝑥) | Reflection over -axis |
𝑎𝑓(𝑥) | Vertical stretch for Vertical compression for |
𝑓(b𝑥) | Horizontal compression for Horizontal stretch for |
Ex. Sketch the graph and find the period and amplitude :
- 𝑓(𝑥) = 2 cos 𝑥 + 3
- 𝑓(𝑥) = 2 sin(3(𝑥 + 𝜋)) − 1
- f(x) = sin(2(x-(π/4))
Solution:
- 𝑓(𝑥) = 2 cos 𝑥 + 3 Can be obtained by vertically stretching the graph of by a scale factor 2 and then shifting it 3 units up
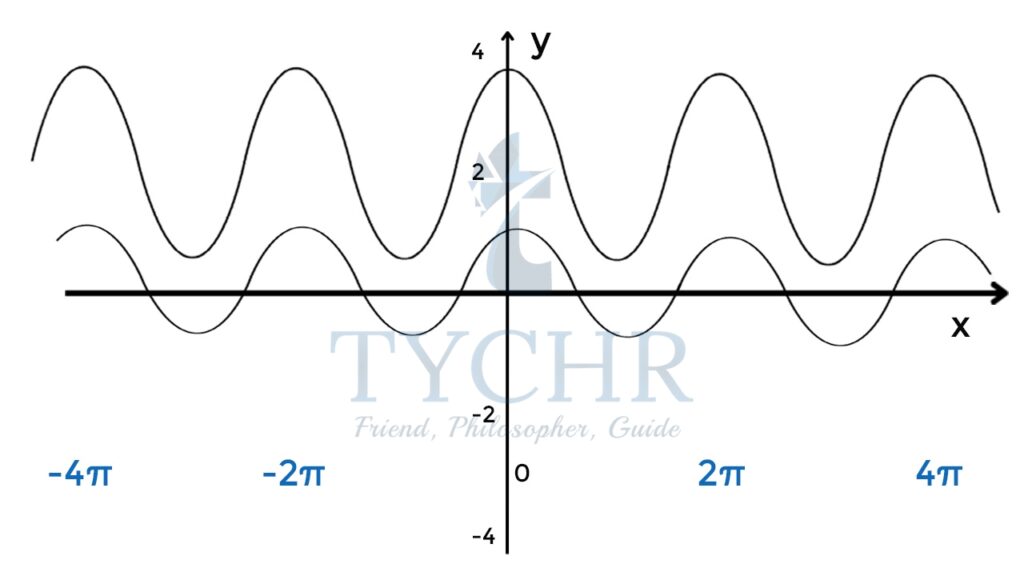
Period-2𝜋
Amplitude- (5 -(1))/2 = 2 - 𝑓(𝑥) = 2 sin(3(𝑥 + 𝜋)) − 1 can be obtained by vertically stretching the graph of , by scale factor 2, then horizontally compressing it by a scale factor 3, then shifting it horizontally by units and finally shifting it 1 unit down.
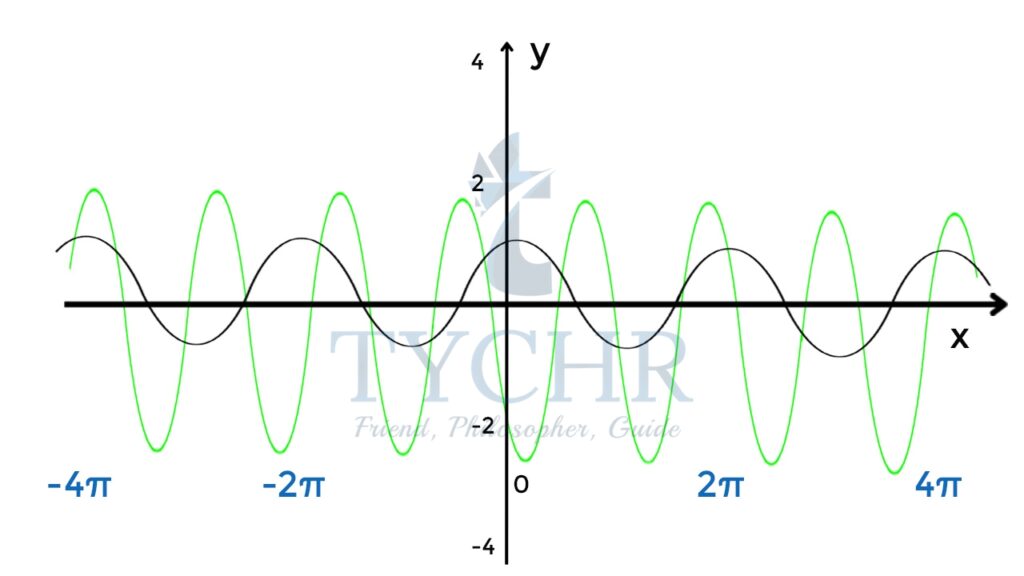
Period-𝜋
Amplitude- (1 -(-3))/2 = 2 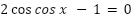 can be obtained by shifting the graph of y= tanx , π/4 units to the right and then horizontally compressing the graph by a scale factor 2.
can be obtained by shifting the graph of y= tanx , π/4 units to the right and then horizontally compressing the graph by a scale factor 2.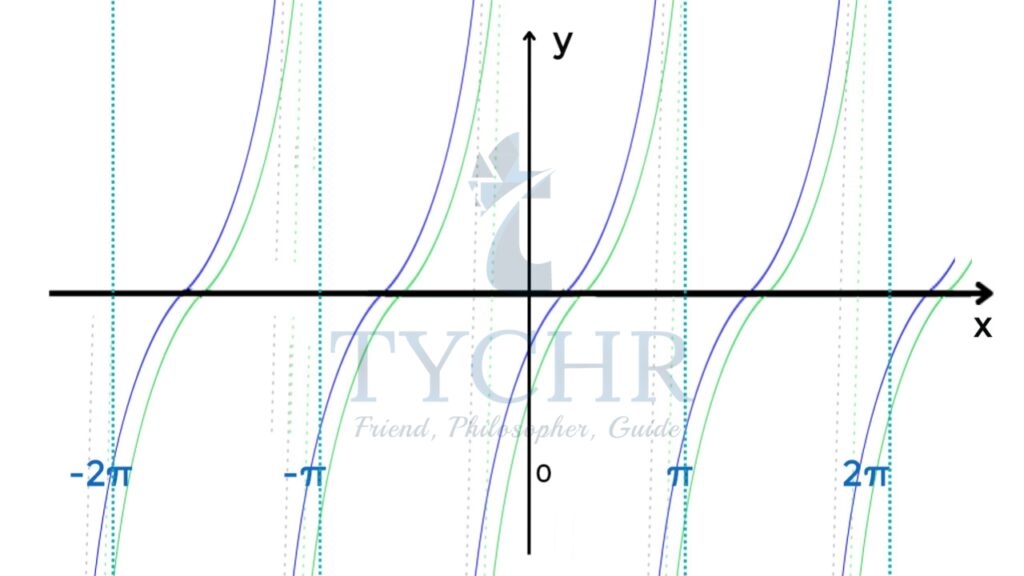
Period-𝜋
TRIGONOMETRIC EQUATIONS AND IDENTITIES
EXACT SOLUTIONS TO TRIGONOMETRIC EQUATIONS
For most trigonometric equations there are infinitely many values of the variable that satisfy the equation In order to restrict the number of solutions, we are asked for the solution to be contained within a suitable interval. Although it is possible to write a general expression using a parameter that specifies the infinite values that solve the given equation (general solution).
We will only deal with the exact solutions. (an interval will always be given)
Ex. Find the excat solution(s) to the equation 2 cos 𝑥 − 1 = 0 for 0 ≤ 𝑥 ≤ 2𝜋 We have – 2 cos 𝑥 − 1 = 0
2cosx = 1
cosx = 1/2
The value of cosine function is 1/2 at π/3 and 5π/3 between 0 and 2𝜋.
x = π/3, 5π/3
We can solve this by considering unit circle as well: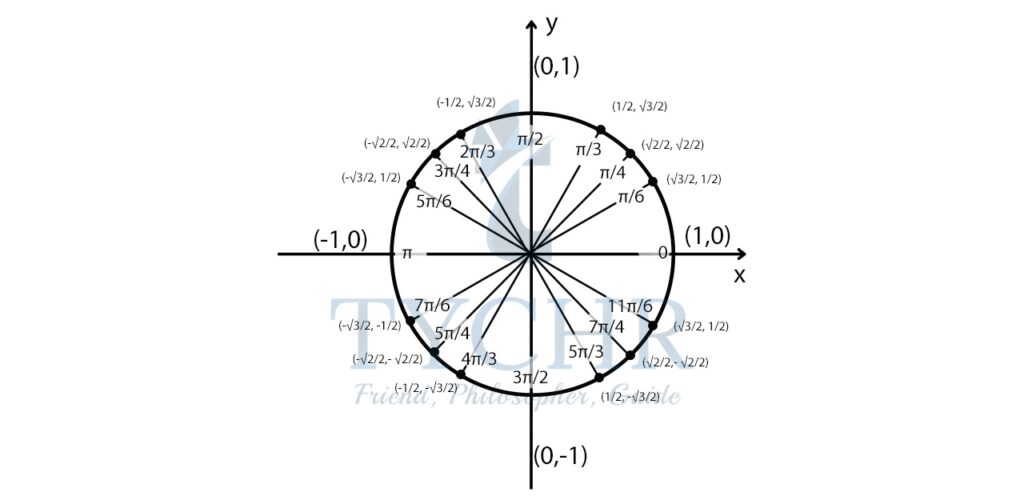
The value of -coordinate (cosine) 1/2 is π/3 at 5π/3
GRAPHICAL SOLUTIONS
Ex. Find the solution(s) to the equation 1 + tan 𝑥 = 0 for −𝜋 ≤ 𝑥 < 𝜋
Graph the equation 1 + tan 𝑥 = 0 and find all the 𝑥-intercepts between – 𝜋 and 𝜋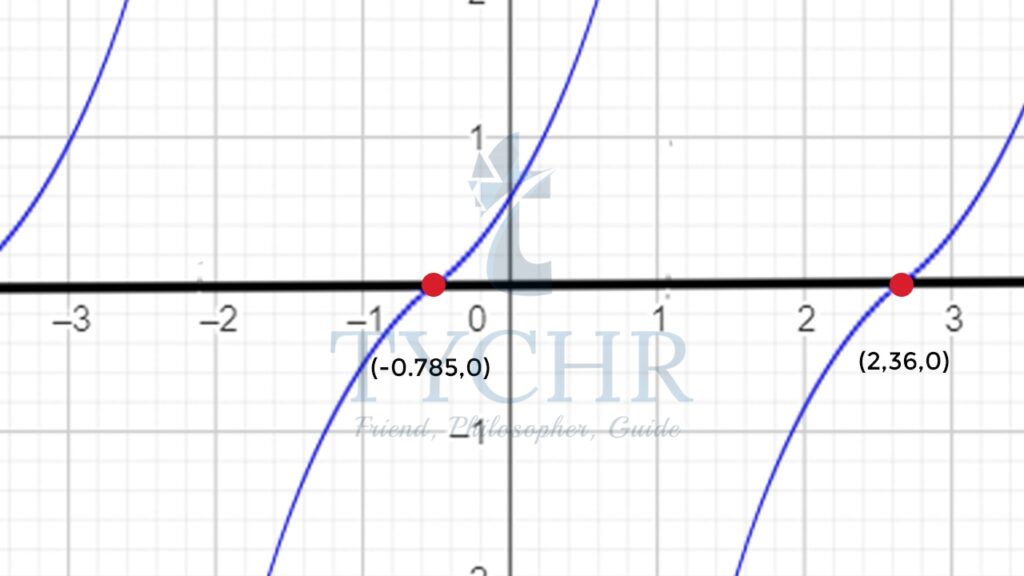 Looking at the graph 𝑥 = 2.36, −0.785
Looking at the graph 𝑥 = 2.36, −0.785
ANALYTIC SOLUTIONS
Ex. Solve 3 sin 𝑥 + tan 𝑥 = 0 for 0 ≤ 𝑥 ≤ 2𝜋
We know that tanx = sinx/cosx
3sinx + (sin/cosx) = 0
3sinxcosx + sinx = 0
sinx(3cosx + 1) = 0
sinx = 0
cosx = (-1/3)
for sin 𝑥 = 0, 𝑥 = 0, 𝜋, 2𝜋
We use the graph of y=cosx and y = -(1/3) and locate the intersection points: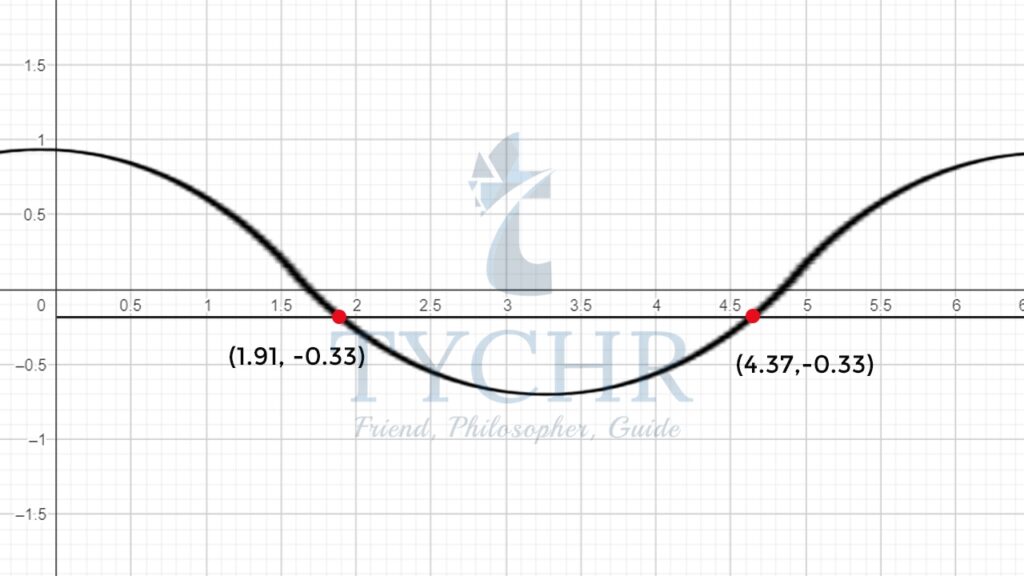 From the graph 𝑥 = 1.91, 4.37
From the graph 𝑥 = 1.91, 4.37
Therefore the full solution set will be – 𝑥 = 0, 𝜋, 2𝜋, 1.91, 4.37
TRIGONOMETRIC IDENTITIES
Pythagorean identity: We know that the unit circle that we consider has the equation:
𝑥2 + 𝑦2 = 1
The -coordinate is the cosine ratio and the -coordinate is the sine ratio, therefore: sin2x + cos2x = 1
sin2x = 1-cos2x
cos2x = 1-sin2x
Double angle identities:
cos2x = cos2x – sin2x
sin2x = 2 sinxcosx
The double angle identity for cosine can be also be written as: (using pythagorean property)
sin2x = (1-cos2x)/2
cos2x = (1+ cosx)/2
Ex. Solve cos2x + sin2x = 1/2 ,0 < x < π/2 Using double angle identity for cosine: cos2x – sin2x + sin2x = 1/2
cos2x =1/2
cos 𝑥 = ±1/√2
But we are given the interval only for the first quadrant, therefore: x = π/4
Ex. Solve -2cos2x -sinx + 1 = 0 , 0 ≤ 𝑥 ≤ 4π,
-2cos2x – sinx + 1 = 0 Using pythagorean property to replace cos2x:
-2(1-sin2x)- sinx +1 = 0
2sin2x – sinx -1 = 0
Factorising:
(2sinx + 1)(sinx -1) =0
sinx = -(1/2), sinx = 1
x = 7π/6 , 11π/6
These are the angles from the unit circle, we will add 2𝜋 to each to get all solutions from 0 to 4𝜋.
x =π/2, 7π/6, 11π/6, 5π/2, 19π/6, 23π/6

