basic geometry and mathematics Notes
BASIC GEOMETRY & MATHEMATICS
By the end of this chapter you should be familiar with:
- Rounding
- Percentage Error
- Rules of Exponents
- Rules of Logarithms
- Angles and Triangles
- Circles
- Volume and Surface area of figures
ROUNDING NUMBERS
Before understanding how to round numbers we need to know what approximations and estimations mean. Approximations are a value or quantity that is nearly but not exactly correct. Estimations are rough calculations of the value, number, quantity, or extent of something. In giving an estimation or approximation, measurements are often rounded to some level of accuracy.
Here’s the general rule for rounding: If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up else you round it down.
Example:
4,827 rounded to the nearest ten is 4,830
4,827 rounded to the nearest hundred is 4,800
4,827 rounded to the nearest thousand is 5,000
PERCENTAGE ERROR
Percentage error expresses as a percentage the difference between an approximate or measured value and an exact or known value.
Percentage Error:
Example: The report said the carpark held 240 cars, but we counted only 200 parking spaces.
Percentage Error = (|Approximate Value − Exact Value|/|Exact Value|) × 100%
(|240 − 200|/|200|) × 100% = 20%
Significant figures are used to express it to the required degree of accuracy, starting from the first non-zero digit.
Law | Example |
All non-zero digits are significant | 74818226 has 8s.f |
All zeros between non-zero digits are significant | 103.05 has 5 s.f |
Zeros to the left of an implied decimal point are non- significant, whereas zeros to the right of an explicit decimal are significant | 23000 has 2 s.f., while 23000.0 has 6 s.f. |
To the right of a decimal point, all leading zeros are non-significant, whereas all zeros that follow non-zero digits are significant | 0.0043 has 2 sf., while 0.0043000 has 5 s.f. |
RULES OF EXPONENTS
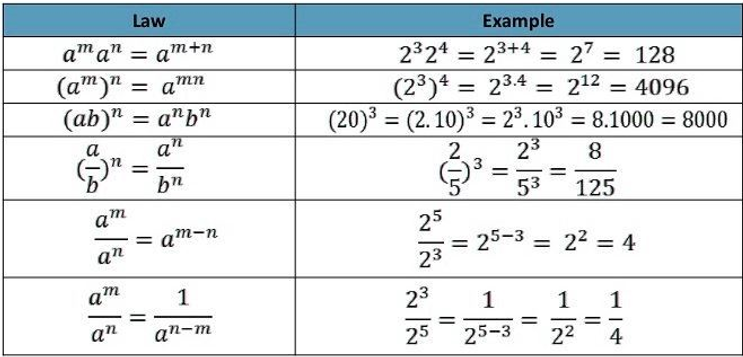
Rule 1: When the numbers having the same base are multiplied, add the exponents.
Rule 2: When the numbers having the same base are divided, subtract the exponents.
Rule 3: Multiply the powers when the numbers are raised by another
RULES OF LOGARITHMS
1)Product Rule: The logarithm of a product is the sum of the logarithms of the factors. loga xy = loga x + loga y
2) Quotient Rule: The logarithm of a quotient is the logarithm of the numerator minus the logarithm of the denominator loga(x/y) = logax – logay
3) Power Rule: loga xn = nlogax
4) Change of Base Rule:
logab =l ogcb/logca
logab = 1/logba
where x and y are positive, and a > 0, a ≠ 1
Example: Simplify the following, expressing each as a single logarithm:
a) log 2 4 + log 2 5
b) log a 28 – log a 4
c) 2 log a 5 – 3log a 2
Solution:
a) log 2 4 + log 2 5 = log 2 (4 × 5) = log 2 20
b) log a 28 – log a 4 = log a (28 ÷ 4) = log a 7
c) 2 log a 5 – 3 log a 2 = log a 52 – log a 23 = log a (25/8)
ANGLES AND TRIANGLES
There are three types of triangles –
Equilateral: “equal”-lateral, so they have all equal sides.
Isosceles: means “equal legs”, they have two equal “sides” joined by an “odd” side.
Scalene: means “uneven” or “odd”, so no equal sides. The sum of the angle of the triangle = 180o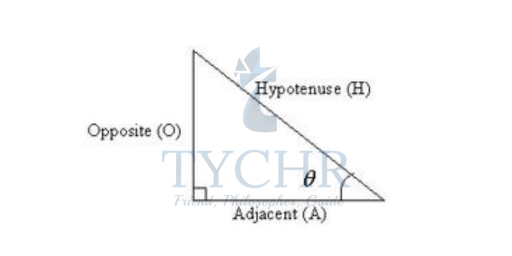
“Opposite” is opposite to the angle θ
“Adjacent” is adjacent (next to) to the angle θ
“Hypotenuse” is the long one
Sin𝜃 = 𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
Cos𝜃 = 𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
Tan𝜃 = 𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒/𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡
Example: How tall is the tree (supposing the triangle is the tree)?
Sin(45°) = 𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
0.7071 = Opposite/20
45o Opposite = 14.14 (to 2 decimals)
Rules when the triangle is not right angled:
If a, b and c are the lengths of the sides opposite the angles A, B and C in a triangle, 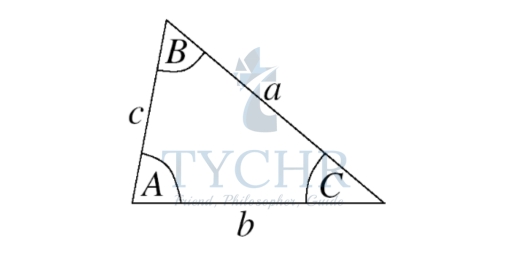
𝑺𝒊𝒏𝑨/𝒂 = 𝑺𝒊𝒏𝑩/𝒃 = 𝑺𝒊𝒏𝑪/𝒄 (sine rule)
c² = a² + b² – 2abcosC (cosine rule)
which can also be written as:
a² = b² + c² – 2bccosA
ANGLE OF ELEVATION AND DEPRESSION:
The term angle of elevation denotes the angle from the horizontal upward to an object. An observer’s line of sight would be above the horizontal.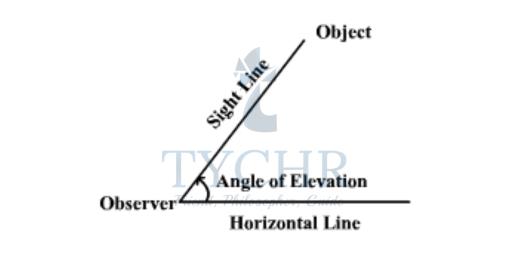 The term angle of depression denotes the angle from the horizontal downward to an object. An observer’s line of sight would be below the horizontal.
The term angle of depression denotes the angle from the horizontal downward to an object. An observer’s line of sight would be below the horizontal. Note that the angle of elevation and the angle of depression are congruent.
Note that the angle of elevation and the angle of depression are congruent.
Example: A man who is 2 m tall stands on horizontal ground 30 m from a tree. The angle of elevation of the top of the tree from his eyes is 28˚. Estimate the height of the tree.
Solution: Let the height of the tree be h. Sketch a diagram to represent the situation.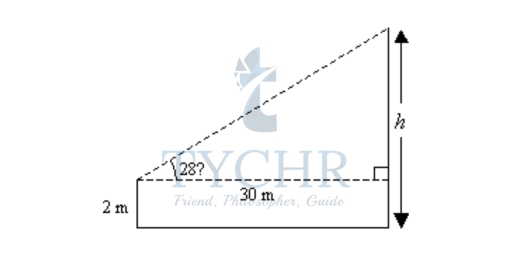
tan 28˚ = (h-2)/30
h – 2 = 30 tan 28˚
h = (30 ´ 0.5317) + 2 ← tan 28˚ = 0.5317 = 17.951
The height of the tree is approximately 17.95 m.
CIRCLES
Area of a circle = πr2
Surface area of a circle = 2πr
The length of arc of a circle with radius “r” and central angle “θ” (in degrees) is = = 𝜽/𝟑𝟔𝟎 × 2πr
The area of the sector with central angle “θ” is = = 𝜽/𝟑𝟔𝟎 × πr2
THREE-DIMENSIONAL GEOMETRY
VOLUME OF 3-D SOLIDS
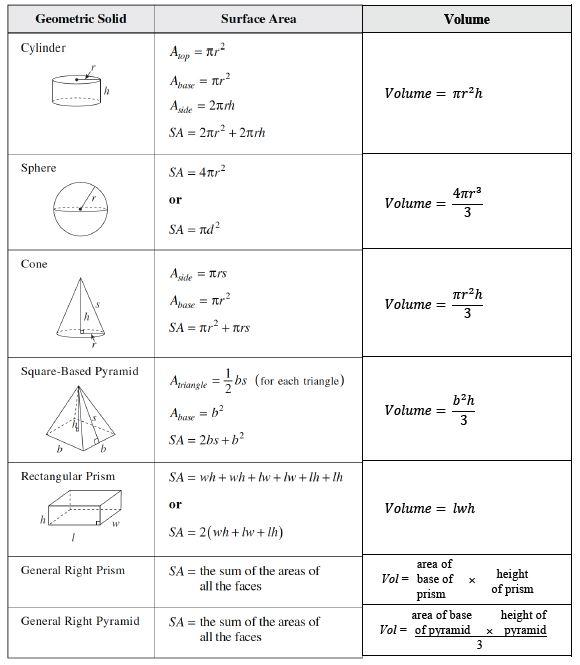
Where r=radius, h=height, w=width, l=length, b=base length
Example 1: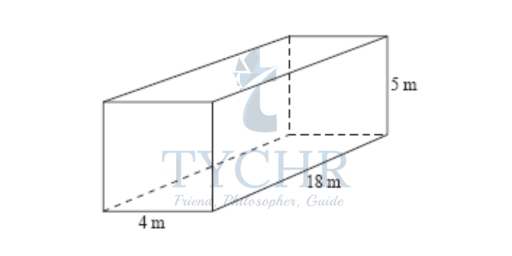
- Calculate the volumeof the cuboid shown. Volume = 4 × 18 × 5 = 360 m³
Surface area = (2 × 4 × 18) + (2 × 4 × 5) + (2 × 5 × 18)
= 144 + 40 + 180
= 364 m² - Calculate the surface areaof the cuboid shown.
Example 2:
Calculate the volume and total surface area of the cylinder shown.
Volume = π r²h = π × 4² × 6 = 96 π
=301.5928947 cm³
=301.5928947 cm³
=302 cm³ (to 3 significant figures)
Area of curved surface = 2π rh = 2 × π × 4 × 6
= 48π
= 150.7964474 cm²
Area of each end = π r² = π × 4²
= 16π
= 50.26548246 cm²
Total surface area = 150.7964474 + (2 × 50.26548246)
= 251.3274123 cm²
= 251 cm² (to 3 significant figures)
Example 3: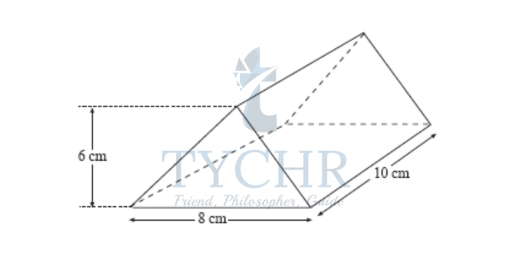
Calculate the volume of this prism.
Area of end of prism = 12 × 8 × 6
= 24 cm²
Volume of prism = 24 × 10
= 240 cm³
