Complex numbers extend the concept of numbers beyond the real numbers, introducing the imaginary unit i, where i² = -1. These numbers are essential tools in various fields, including mathematics, physics, and engineering. This study note explores the fundamental concepts of complex numbers within the context of the IBDP Mathematics: Applications and Interpretation HL syllabus, covering topics such as complex number representation, operations, polar form, De Moivre’s theorem, and applications. A strong understanding of complex numbers is crucial for success in the AI HL course.

By the end of this chapter you should be familiar with:

• The properties of complex numbers
• Cartesian form of complex numbers
• Polar form of complex numbers
• Exponential form of complex numbers
• Powers and roots of complex numbers
• The use of complex numbers in STEM applications

Real numbers are simply the combination of rational and irrational numbers, in the number system. Complex numbers cannot be represented on the number line, but are analytic solutions to equations whose solutions are not real numbers. These complex numbers have an imaginary unit.

IMAGINARY NUMBERS

A number that is expressed in terms of the square root of a negative number is called an imaginary number. The imaginary unit is i and i = √(-1)

PROPERTIES:

• i = √(-1)
• i² = -1
• i³ = -i
• i⁴ = 1, then i⁵ = i and so on for iⁿ

Every power n is an integer multiple of four that produces iⁿ = 1 and the pattern repeats.

Example: Express each in its simplest form
a) i³² = i⁴ = 1
b) i¹²⁶ = i² = -1

Complex number has two parts, a real part and an imaginary part which can be thought of as two- dimensional numbers. This concept can be understood by placing them in the complex plane called the argand plane. A complex number has the form z = a + bi.

|z| is the modulus of the complex number and the argument of z is defined as the angle between the positive real axis and the line from origin to z.

Example:Find the zeros of the equation y = x² – 2x + 5 and find the modulus and argument of the zeros.

Solution: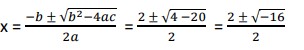 Arg(x) = tan^-1(2/1) = 63.435^o

When a quadratic polynomial in x has zeros r₁ and r₂ then (x – r₁) and (x – r₂) are its factors. Then the quadratic equation is = x² – (r₁ + r₂)x + r₁r₂ Therefore, we can conclude that the negative sum of the zeroes is the coefficient of x and the product of the zeros is the constant term.

The complex conjugate of z = a + bi is z^* = a – bi and the product of zz^* is (a + bi)(a – bi) = a² + b²

Example: Rationalize in the form a + bi.

Solution: 6/(1+𝑖) = (6/(1+𝑖)) × ((1−𝑖)/(1− 𝑖)) = 6(1−𝑖)/2
= 3(1 – i) = 3 – 3i

POLAR FORM OF COMPLEX NUMBERS

The polar form of a complex number z = a + bi is z = r(cosθ + isinθ) and can be abbreviated as z = r cis  

where r=|z|= √(𝒂^𝟐 + 𝒃^𝟐)(modulus) a = rcosθ and b = rsinθ
θ = tan^-1(b/a) (argument also referred to as arg(z)) for a > 0 and = tan^-1(b/a) + πor θ = tan^-1(b/a) + 180° for a < 0. 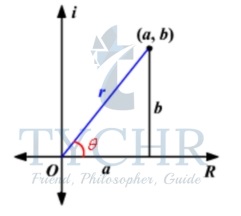Example: Express 5 + 2i complex number in polar form.

Solution: The polar form of a complex number z = a + bi is z=r(cosθ + isinθ).
So, first find the absolute value of r.
r=|z|= √(𝒂^𝟐 + 𝒃^𝟐) = √(5^𝟐 + 2^𝟐) = √29 = 5.39
Now find the argument θ.
Since a > 0, use the formula θ=tan^-1(b/a).
θ = tan^-1(2/5) = 0.38

Note that here θ is measured in radians.

Therefore, the polar form of 5 + 2i is about 5.39(cos(0.38) + isin(0.38)).

EULER FORM OF COMPLEX NUMBERS

Euler’s formula is the statement that e^iθ= cos(θ) + isin(θ). When x = π, we get Euler’s identity, e^iπ = -1, or e^iπ + 1 = 0. Basically, z = a + bi = re^iθ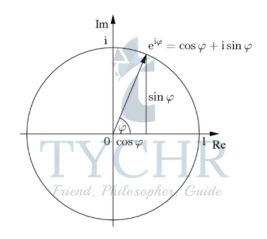Example: Taking the last example where we found r = 5.39 and = 0.38.5 + 2i can also be expressed in Euler’s form as z = 5.39 e^i0.38

POWERS OF COMPLEX NUMBERS

DeMoivre’s Theorem states that zⁿ = (re^iθ)ⁿ = rⁿe^iθ
or zⁿ = rⁿ cis(nθ)

Example: Compute (3 + 3i)⁵

r=|z|= √(𝒂^𝟐 + 𝒃^𝟐) = √(3^𝟐 + 3^𝟐) = 3√2 = tan^-1(3/3) = π/4
zⁿ = (re^iθ)ⁿ
(3 + 3i)⁵ = (3√2)⁵ 𝑒^{𝑖 5𝜋/4} = 972√2(cos(5π/4) + i sin(5π/4)) = -972 – 972i

APPLICATIONS OF COMPLEX NUMBERS

REPRESENTING VOLTAGES IN COMPEX PLANE

Using the complex plane, we can represent voltages across resistors, capacitors and inductors.

The voltage across the resistor is regarded as a real quantity, while the voltage across an inductor is regarded as a positive imaginary quantity, and across a capacitor we have a negative imaginary quantity. Our axes are as follows:All AC waveforms have sinusoidal curves.

IMPEDANCE AND PHASE ANGLE

The impedance of a circuit is the total effective resistance to the flow of current by a combination of the elements of the circuit.

To find this total voltage, we cannot just add the voltages V_R, V_L and V_C.

Because V_L and V_C are considered to be imaginary quantities, we have:

Impedance V_RLC = IZ

Z = R + j(X­_L ​– X_C​)

|Z| =√𝑹^𝟐 + (𝑿_𝑳 − 𝑿_𝑪)^𝟐

tan θ = (𝑿_𝑳 − 𝑿_𝑪)/𝑹

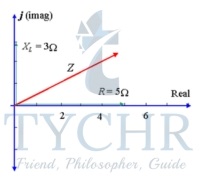
Example: A circuit has a resistance of 5Ω in series with a reactance across an inductor of 3Ω. Represent the impedance by a complex number, in polar form.

Solution: In this case, X_L​= 3Ω and X_C ​= 0 so X_L ​– X_C​ = 3 Ω.
So in rectangular form, the impedance is written: Z=5+3j Ω

Using calculator, the magnitude of Z is given by: 5.83, and the angle θ is given by: 30.96∘.

So, the voltage leads the current by 30.96∘, as shown in the diagram.
Presenting Z as a complex number (in polar form), we have: Z=5.83∠30.96∘ Ω.

Complex numbers are powerful mathematical tools with wide-ranging applications. This study note has covered the key concepts of complex numbers relevant to the IB DP Mathematics: Applications and Interpretation HL syllabus. Practice applying these concepts to various problems is essential for solidifying your understanding. For personalized support in IB DP Mathematics AI HL, including complex numbers and other topics, consider working with a tutor. TYCHR connects students with experienced IB Mathematics AI HL tutors who can provide tailored assistance. A strong foundation in complex numbers is essential for success in IB DP Mathematics AI HL.