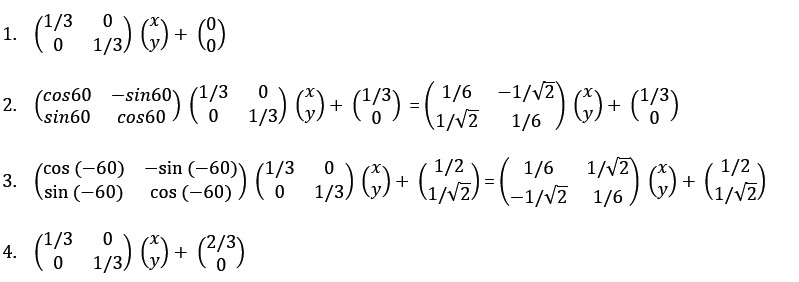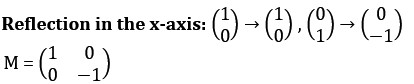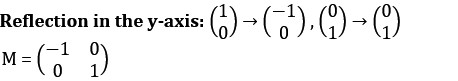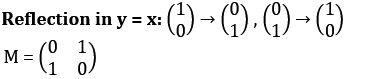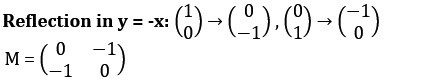Matrix And Algebra Notes
By the end of this chapter you should be familiar with:
- Matrix, its order and elements
- Algebra of matrices
- Determinant
- Inverse
- Linear System
- Eigenvectors and Eigenvalues
- Diagonalization
- Transformations
- Applications
MATRIX DEFINITIONS AND OPERATIONS
Matrix refers to an ordered rectangular arrangement of numbers which are either real or complex or functions. We enclose Matrix by [ ] or ( ) where ai,j represents the element located in row i and column j.

Different types of matrices are:
- Row matrix – A row matrix has only one row but any numberof columns. A matrix is said to be a row matrix if it has only one row. For example, A = [−1/2 √5 2 3] is a row matrix of order 1 × 4. In general, A = [aij]1 × n is a row matrix of order 1 × n.
- Column matrix – A column matrix has only one column but any number of rows. A matrix is said to be a column matrix if it has only one column. For example, A =[ 3 3 1] is a column matrix of order 3 × 1. In general, B = [bij]m × 1 is a column matrix of order m × 1.
- Square matrix – A square matrix has the number of columns equal to the number of rows. A matrix in which the number of rows is equal to the number of columns is said to be a square Thus, an m × n matrix is said to be a square matrix if m = n and is known as a square matrix of order ‘n’. For example,
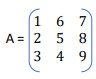 is a square matrix of order 3. In general, A = [aij] m × m is a square matrix of order m. And if it doesn’t have equal number of rows and columns then it is called a rectangular matrix.
is a square matrix of order 3. In general, A = [aij] m × m is a square matrix of order m. And if it doesn’t have equal number of rows and columns then it is called a rectangular matrix.
- Diagonal matrix – A square matrix B = [bij] m × m is said to be a diagonal matrixif all its non-diagonal elements are zero, that is a matrix B =[bij]m×m is said to be a diagonal matrix if bij = 0, when i ≠ j. For example, A = [1 0 0 1] where A is also known as an identity matrix as it has all 1’s in its diagonal.
- Zero Matrix – A matrix is said to be zero matrix or null matrix if all its elements are zero.
For Example, A = [0] where A is of order 1.
- Upper Triangular matrix – A square matrix in which all the elements below the diagonal are zero is known as the upper triangular matrix. For example,

- Lower Triangular matrix – A square matrix in which all the elements above the diagonal are zero is known as the upper triangular matrix. For example,
ADDING AND SUBTRACTING MATRICES
The addition of two matrices A m*n and Bm*n gives a matrix Cm*n. The elements of C is the sum of corresponding elements in A and B which can be shown as
The subtraction of two matrices Am*n and Bm*n gives a matrix Cm*n. The elements of C are difference of corresponding elements in A and B which can be represented as:
Addition of matrices is commutative which means A+B = B+A Addition of matrices is associative which means A+(B+C) = (A+B)+C whereas subtraction is neither. The matrices must have the same order to be computed.
SCALAR MULTIPLICATION
Scalar multiplication refers to the product of a real number and a matrix. In scalar multiplication, each entry in the matrix is multiplied by the given scalar.
Example: A = [1 2 0 1]
then 2A = [2 4 0 2]
MULTIPLACTION OF MATRICES
The multiplication of two matrices Am*n and Bn*p gives a matrix Cm*p. It means number of columns in A must be equal to number of rows in B to calculate C=A*B. To calculate element c11, multiply elements of 1st row of A with 1st column of B and add them (5*1 + 6*4) which can be shown as:
Multiplication of matrices is non-commutative which means A*B ≠ B*A Multiplication of matrices is associative which means A*(B*C) = (A*B)*C
But, A × I = I × A = A where I is the identity matrix.
Example: From the given data find the final grades of the following students
Student | Tests | Projects | Homework | Quizzes |
Alexandra | 92 | 100 | 89 | 80 |
Megan | 72 | 85 | 80 | 75 |
Brittney | 88 | 78 | 85 | 92 |
Type | Weight |
Tests | 40% |
Projects | 15% |
Homework | 25% |
Quizzes | 20% |
Solution:
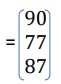
Alexandra has a 90, Megan has a 77, and Brittney has an 87.
DETEREMINANT AND INVERSES
The determinant of the 2 × 2 matrix A = ( 𝑎 𝑏 𝑐 𝑑 ) is the number ad – cb. The above sentence is abbreviated as det(A) = ad – cb
If the determinant of the matrix 0, then the inverse of the matrix exists.
For a 2 × 2 matrix A = the inverse is given as: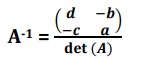 For a 3 × 3 matrix, We can find A-1 in such a way that AA-1 = I or we can use the calculator.
For a 3 × 3 matrix, We can find A-1 in such a way that AA-1 = I or we can use the calculator.
For determinant we can use the given formula: Note: (PQ)-1 = Q-1P-1 P-1Q-1
Note: (PQ)-1 = Q-1P-1 P-1Q-1
LINEAR SYSTEM
A given set of equations can be written in matrix form given by: AX = B where A contains the matrix of coefficients of x and y. X contains a matrix x and y and B contains the matrix of the constants.
Example: Solve the system of equations using matrices. 2x + 3y = 3 and x – y =4
Solution: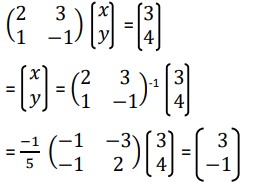
Therefore, x = 3 and y = -1.
There is a solution to the system when A is non-singular. If B = 0, the system is homogeneous. A homogeneous system will always have a solution, called the trivial solution, X = 0 when A is non-singular. When A is singular then the system has infinitely many solutions.
AREA OF TRIANGLE
We can find the area of the triangle using determinants.
Example: Find the area of the triangle ABC whose vertices are A(1,3) , B(5,-1) and C(-2,5)
Solution: 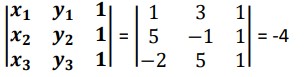
Area = |1/2 × determinant value| = 2
LINES
For lines in plane,
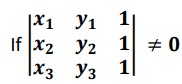 then the points cannot lie on a line but if the determinant value is 0 then the points lie on the line.
then the points cannot lie on a line but if the determinant value is 0 then the points lie on the line.
To find the two-point equation of a line we use: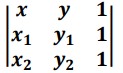
CRYPTOGRAPHY
The process of encryption is known as cryptography. Here, we are going to use Hill Cypher.
Lets take an example to understand the working.
For ease, we will use a 2×2 key matrix for the encryption. The message we want to encrypt is “UTES”. Since our key matrix is 2×2, we must split the message into chunks of two letters. This is true for all matrices, so for an NxN matrix, the message would be split into chunks of N letters. Each letter in the message is assigned a numerical value, ranging from 0 up to the modular base. For our encryption, we will use the letters A-Z (so the modulus is 26). While in practice the letters can be assigned any value (as long as the sender and recipient both know the corresponding values), we will use the straightforward approach. So, A = 0, B = 1, C = 2, etc. all the way to Z = 25. Below we see how our message is assigned:
𝑈𝑇𝐸𝑆 = ( 20 19) , ( 4 18)
Our key matrix K for this example will be: 𝐾 = ( 4 1 3 7 )
Note that the key matrix must be known by the receiver in order to decode the message.
Now for each chunk of our message, we perform a matrix multiplication against the key matrix.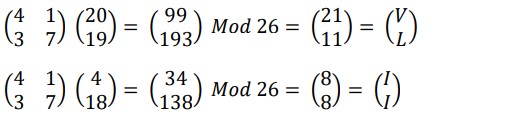
Our encrypted message is VLII.
For decrypting this we find K-1 and multiply it with ( 21 11) and ( 8 8 ) to get back our original matrices which says UTES.
GAUSS-JORDON ELIMINATION
Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix:
- Swap the positions of two of the rows
- Multiply one of the rows by a nonzero scalar.
- Add or subtract the scalar multiple of one row to another row.
Example: Use Gauss-Jordan elimination to solve the system: x + 3y + 2z = 2, 2x + 7y + 7z = −1 and 2x + 5y + 2z = 7
Solution: The augmented matrix of the system is 
 Therefore, x = 3, y = 1 and z = -2
Therefore, x = 3, y = 1 and z = -2
ROW REDUCED ECHELON FORM
The purpose of Gauss-Jordan Elimination is to use the three elementary row operations to convert a matrix into reduced-row echelon form. A matrix is in reduced-row echelon form, also known as row canonical form, if the following conditions are satisfied:
- All rows with only zero entries are at the bottom of the matrix
- The first nonzero entry in a row, called the leading entry or the pivot, of each nonzero row is to the right of the leading entry of the row above it.
- The leading entry, also known as the pivot, in any nonzero row is 1.
- All other entries in the column containing a leading 1 are zeroes.
In the previous example, the row reduced echelon form was 
EIGENVECTORS AND EIGENVALUES
An eigenvector of a matrix A is a vector whose product when multiplied by the matrix is a scalar multiple of itself. The corresponding multiplier is often denoted as and referred to as an eigenvalue.
A·v = λ·v
In this equation A is an n-by-n matrix, v is a non-zero n-by-1 vector and λ is a scalar (which may be either real or complex). Any value of λ for which this equation has a solution is known as an eigenvalue of the matrix A. It is sometimes also called the characteristic value. The vector, v, which corresponds to this value is called an eigenvector. The eigenvalue problem can be rewritten as
A·v – λ·v=0
A·v – λ·I·v=0
(A – λ·I)·v=0
If v is non-zero, this equation will only have a solution if
|A – λ·I|=0
This equation is called the characteristic equation of A, and is an nth order polynomial in λ with n roots. These roots are called the eigenvalues of A. We will only deal with the case of n distinct roots, though they may be repeated. For each eigenvalue there will be an eigenvector for which the eigenvalue equation is true.
Example: Find eigenvalues and eigenvectors of ![]()
Solution: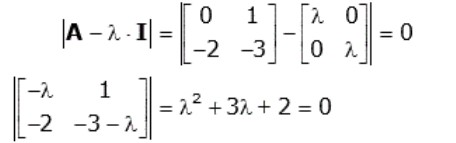
and the two eigenvalues are λ1=-1, λ2=-2
All that’s left is to find the two eigenvectors. Let’s find the eigenvector, v1, associated with the eigenvalue, λ1=-1, first.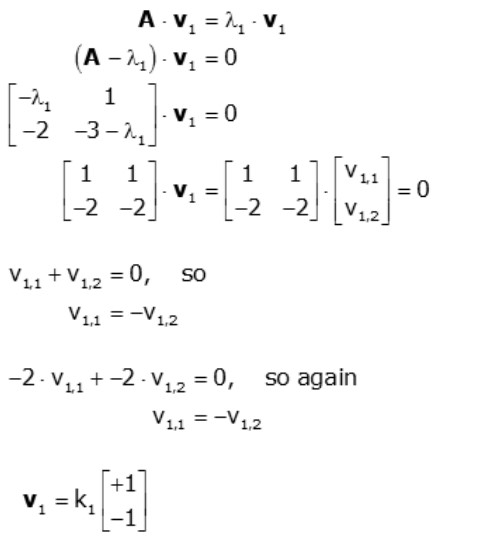
where k1 is an arbitrary constant. Note that we didn’t have to use +1 and -1, we could have used any two quantities of equal magnitude and opposite sign.
Going through the same procedure for the second eigenvalue: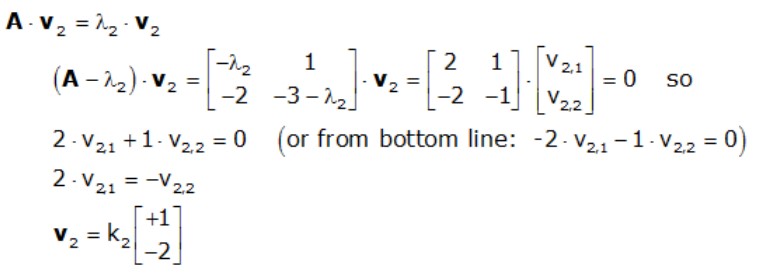
DIAGONALIZATION
An n × n matrix A is diagonalizable if it is similar to a diagonal matrix: that is, if there exists an invertible n × n matrix P and a diagonal matrix D such that
A = PDP-1
An = PDnP-1
where D is a diagonal matrix containing the eigenvalues and P is a matrix containing eigenvectors.
We can use the above example and prove that PDP-1 would give us A back.
MATRICES AND GEOMETRIC TRANSFORMATIONS
The method we can use to find the matrix representing a transformation is given by the Matrix Basis theorem.
Let T be a transformation represented by a matrix M:
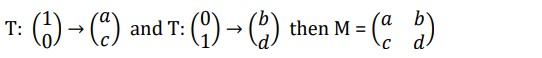
AFFINE TRANSFORMATIONS
In order to incorporate the idea that both the basis and the origin can change, we augment the linear space u, v with an origin o. Note that while u and v are basis vectors, the origin o is a point. We call u, v, and t (basis and origin) a frame for an affine space. Then, we can represent a change of frame as:
p’ = x.u + y.v + o
The two types of special affine transformations are rotations and translations.
To rotate use the matrix ![]()
A translation of h units horizontally and k units vertically is achieved by: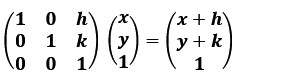 Example: The square PQRS with vertices P(-2,4), Q(-6,-3), R(1,-7), S(5,0) undergoes a transformation described by
Example: The square PQRS with vertices P(-2,4), Q(-6,-3), R(1,-7), S(5,0) undergoes a transformation described by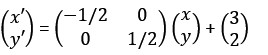 Determine the coordinates of the vertices of the image PQRS and graph it.
Determine the coordinates of the vertices of the image PQRS and graph it.
Solution: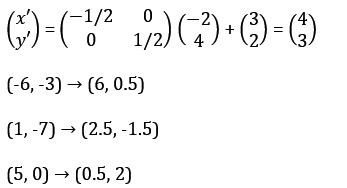
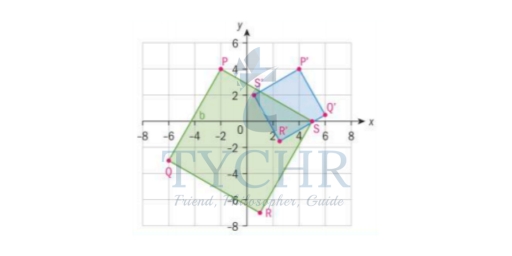
If two transformation are S and T then S o T is known as a composition of two transformations.
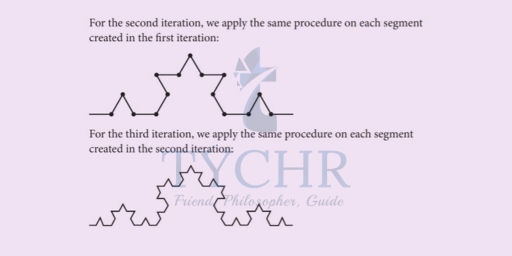
FRACTALS
The 8 transformation equations used to generate this image are:
Example:
Solution: