Probability Distributions Notes
By the end of this chapter you should be familiar with:
- Continuous and discrete variables
- Mean and variance of a binomial distribution
- Mean and variance of Poisson distribution
- Mean and variance of a normal distribution
- Linear transformation
- Combination of data
- Markov chains
RANDOM VARIABLES
They can be discrete or continuous. All the probability distributions that we are going to discuss come under discrete random variable (DRV).
The assignment of a value to every possible outcome of a random experiment is called random variable. Mathematically random variable is a function from the set of all sample space to the set of all real numbers.
DISCRETE RANDOM VARIABLE
If a random variable takes an integer value then it is called a discrete random variable or a random variable is only discrete if and only if its range is countable.
If X is a discrete random variable with range Rx = {x1, x2, …., xn} then the function Px(xk) = P(X = xk) for all k = 1, 2, 3… is called a probability mass function. The properties are:
- 0 ≤ Px(xi) ≤ 1
- ∑𝑛𝑖=1𝑃𝑥(xi) = 1
If x is a random variable then mean or expected value of discrete random variable is denoted by![]() The variance of a discrete random variable measures the spread or the variability of the distribution and is denoted by
The variance of a discrete random variable measures the spread or the variability of the distribution and is denoted by ![]()
Standard deviation is 𝜎x
As we already know, if F(x) = P(X ≤ x)
∑𝑛𝑖=1𝑃𝑥( xi) and P(X > x) = 1 – xi)
Example: Let x be a DRV with range Rx = {1, 2, 3…}. Suppose PMF of x is given by Px(k) = 1/2k for k = 1, 2, 3…. Find
a. P(2 < X ≤ 5)
b. P(X > 4)
Solution:
- P(2 < X ≤ 5) = P(3) + P(4) + P(5)
= 1/23 + 1/24 + 1/25
= 7/32 - P(X > 4) = 1 – P(X ≤ 4)
= 1 – [P(1) + P(2) + P(3) + P(4)]
= 1 – [1/2 + 1/22 + 1/23 + 1/24]
= 1/16
CONTINUOUS RANDOM VARIABLE
If a random variable takes all possible values between two limits or if it represents a real number then the random variable is called a continuous random variable.
BINOMIAL DISTRIBUTION
A random experiment which has only two possible outcomes is called the Bernoulli’s trail. If p represents the probability of success and q the probability of failure then the mean and variance and the probability distribution is given by: E(X) =𝜇 = np
Var(X) = 𝜎2= npq
P(x) = b(n,p,x) = nCx px (1 – p)n-x
Example: If the mean and variance of correctly answered questions in a test given to 4096 students are 2.5 and 1.875. Find and estimate of the number of students answering
- 2 or less correctly
- 5 questions correctly
Solution: 𝜇 = np, 2.5= np, 𝜎= npq 1.875 = 2.5q
q = 0.75, p = 1 – q = 0.25 , n= 10
- P(X ≤ 2) = P(1) + P(2) + P(3)
= 10C1 (0.25)1 (0.75)10 – 1 + 10C2 (0.25)2 (0.75)10 – 2 + 10C3 (0.25)3 (0.75)10 – 3
= 0.719 - P(X = 5) = 10C5 (0.25)5 (0.75)10 – 5 = 0.0583
POISSON DISTRIBUTION
Poisson distribution gives the probability of happening of the number of events occurring in a fixed interval of time, space or any other parameter with a known average. The mean, variance and the probability distribution is given by:
E(X) = 𝜇 = np
Var(X) = 𝜎2= 𝜇
P(x) = p( 𝜇, x) = 𝑒−𝜇 𝜇𝑥/𝑥!
Example: The number of accidents in a year to the taxi drivers in the city follow Poisson distribution with = 3. Out of 1000 taxi drivers find approximately the number of drivers with
- No accident in a year
- More than 3 accidents in a year
Solution:
- P(0) = e-3 = 0.0497 × 1000 = 50
- P(X > 3) = 1 – P(X ≤ 3)
= 1 – [P(0) + P(1) + P(2) + P(3)]
= 1 – e-3[ 1 + 3 + 4.5 + 4.5]
= 0.35276 × 1000
= 353
NORMAL DISTRIBUTION
A normal distribution is a binomial distribution for a very large n and the probability success is close to half. Given set of data is said to be normally distributed if the weight at which the frequencies fall off is proportional to the distance from the mean and frequencies themselves. The distribution is given by: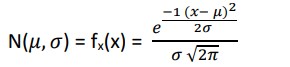 where x can be any value between -∞ to ∞, 𝜎 is always positive and mean can also be any value between -∞ to ∞. The graph of a normal distribution is called a bell curve which is symmetric about the mean.
where x can be any value between -∞ to ∞, 𝜎 is always positive and mean can also be any value between -∞ to ∞. The graph of a normal distribution is called a bell curve which is symmetric about the mean.
The normal distribution for which 𝜇 = 0 and 𝜎 = 1 is called standard normal distribution or the z distribution and z = (𝑥− 𝜇)/𝜎
Example: If x is a random variable which is distributed normally with = 60 and = 5. Find the probability of
- 60 ≤ X ≤ 70
- X ≤ 50
- X > 40
Solution:
- z = (𝑥− 𝜇)/𝜎 = (x – 60)/5
p(0 ≤ z ≤ 2) = A(2) = 0.4772 - z = -2
p(z ≤ 0) – p(-2 ≤ z ≤ 0)
= 0.5 – 0.4772 = 0.0228 - z = -4
p(z ≥ 0) + p(0 ≤ z ≤ 4) = 0.5 + 0.4996 = 0.996
LINEAR TRANSFORMATION
A linear transformation is a change to a variable characterized by one or more of the following operations: adding a constant to the variable, subtracting a constant from the variable, multiplying the variable by a constant, and/or dividing the variable by a constant.
When a linear transformation is applied to a random variable, a new random variable is created. To illustrate, let X be a random variable, and let m and b be constants. Each of the following examples show how a linear transformation of X defines a new random variable Y.
- Adding a constant: Y = X + b
- Subtracting a constant: Y = X – b
- Multiplying by a constant: Y = mX
- Dividing by a constant: Y = X/m
- Multiplying by a constant and adding a constant: Y = mX + b
- Dividing by a constant and subtracting a constant: Y = X/m – b
EFFECT ON MEAN AND VARIANCE
Suppose a linear transformation is applied to the random variable X to create a new random variable Y. Then, the mean and variance of the new random variable Y are defined by the following equations.
Y̅ = mX̅ + b and Var(Y) = m2 Var(X)
where m and b are constants,Y̅ is the mean of Y, X̅ is the mean of X, Var(Y) is the variance of Y, and Var(X) is the variance of X.
Example: The average salary for an employee at Acme Corporation is $30,000 per year. This year, management awards the following bonuses to every employee.
- A Christmas bonus of $500.
- An incentive bonus equal to 10 percent of the employee’s salary.
What is the mean bonus received by employees?
Solution: Y = mX + b
Y = 0.10 X + 500 where Y is the transformed variable (the bonus), X is the original variable (the salary), m is the multiplicative constant 0.10, and b is the additive constant 500.
Since we know that the mean salary is $30,000, we can compute the mean bonus from the following equation.
Y̅ = mX̅ + b
Y̅ = 0.10 $30,000 + $500 = $3,500
RANDOM VARIABLE COMBINATIONS
EFFECT ON MEAN
Suppose you have two variables: X with a mean of μx and Y with a mean of μy. Then, the mean of the sum of these variables μx+y and the mean of the difference between these variables μx-y are given by the following equations.
μx+y = μx + μy and μx-y = μx – μy
The above equations for general variables also apply to random variables. If X and Y are random variables, then
E(X + Y) = E(X) + E(Y) and E(X – Y) = E(X) – E(Y)
where E(X) is the expected value (mean) of X, E(Y) is the expected value of Y, E(X + Y) is the expected value of X plus Y, and E(X – Y) is the expected value of X minus Y.
EFFECT ON VARIANCE
Suppose X and Y are independent random variables. Then, the variance of (X + Y) and the variance of (X – Y) are described by the following equations
Var(X + Y) = Var(X – Y) = Var(X) + Var(Y)
where Var(X + Y) is the variance of the sum of X and Y, Var(X – Y) is the variance of the difference between X and Y, Var(X) is the variance of X, and Var(Y) is the variance of Y.
Note: The standard deviation (SD) is always equal to the square root of the variance (Var). Thus,
SD(X + Y) = sqrt[ Var(X + Y) ] and SD(X – Y) = sqrt[ Var(X – Y) ]
Example: Suppose X and Y are independent random variables. The variance of X is equal to 16; and the variance of Y is equal to 9. Let Z = X – Y. What is the standard deviation of Z?
Solution: The solution requires us to recognize that Variable Z is a combination of two independent random variables. As such, the variance of Z is equal to the variance of X plus the variance of Y.
Var(Z) = Var(X) + Var(Y) = 16 + 9 = 25
The standard deviation of Z is equal to the square root of the variance. Therefore, the standard deviation is equal to the square root of 25, which is 5.
MARKOV CHAINS
A Markov chain is a mathematical system that experiences transitions from one state to another according to certain probabilistic rules.
A Markov chain is a stochastic process, but it differs from a general stochastic process in that a Markov chain must be “memory-less.” That is, (the probability of) future actions are not dependent upon the steps that led up to the present state. This is called the Markov property.
A transition matrix T for Markov chain at time t is a matrix containing information on the probability of transitioning between states.
xn = x0 Tn
Lets take an example to understand better
Example: Consider the Markov chain with three states, S = {1,2,3}, that has the following transition matrix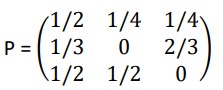
- Draw the state transition diagram for this chain.
- If we know P(X1 = 1) = P(X1 = 2) = 1/4, find P(X1 = 3, X2 = 2, X3 = 1)
Solution:
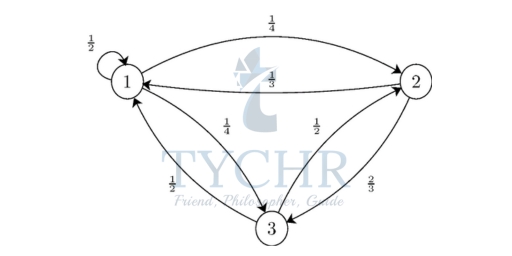
- First, we obtain
P(X1 = 3) = 1 − P(X1 = 1) − P(X1 = 2) = 1 – 1/4 – 1/4 = ½
We can now write
P(X1 = 3,X2 = 2,X3 = 1) = P(X1 = 3)⋅p32⋅p21
= (1/2) (1/2) (1/3) = 1/12.
