Engineering Physics Theory Notes
Rigid body and rotational dynamics
Centripetal force:
For a body of mass m moving in a circle of radius r with a uniform speed v and angular velocity has an acceleration 𝑣2/𝑟= 𝑟𝜔2 towards the centre and force 𝑚𝑣2/𝑟 acts on it.
Equations of motion:
The equations of motion for rotational motion are similar to those of linear motion.
𝜔𝑓 = 𝜔𝑖 + 𝛼𝑡
𝜃 = 𝜔𝑖𝑡 +(1/2)𝛼𝑡2
𝜔𝑓2 = 𝜔𝑖2 + 2𝛼𝜃
𝜃 =(𝜔𝑓 + 𝜔𝑖)𝑡/2
These apply to the case of constant acceleration.
Moment of inertia:
Moment of inertia is the inertial equivalent of mass in rotational dynamics.
Moment of inertia of a particle of mass m rotating in a circle of radius r has moment of inertia mr2. For a group of particles, it is given by Σ𝑚𝑟2.
Torque:
Torque causes rotation.
Consider a force F acting on a body at an angle to the radius of circle in which it rotates. The torque acting at a distance r from the point of rotation is 𝐹𝑟𝑠𝑖𝑛𝜃.
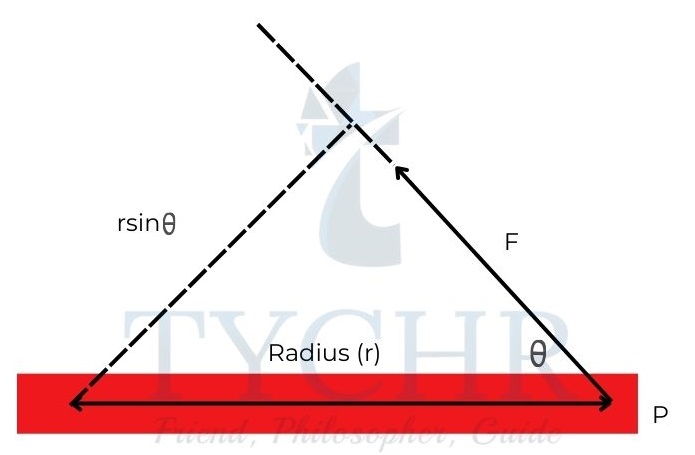
The maximum torque (Fr) acts on a body when the force applied is perpendicular to the radius.
Couple:
A couple is said to act on a body when two forces of equal magnitude act on the body in opposite directions. For a non-zero couple, the forces should not act on a straight line. Here the net force acting is zero. So, there will be no linear motion produced by the couple.
The magnitude of a couple whose magnitude of force is F and distance between the lines of action of forces is d is Fd.
When a torque T acts on a body, the angular acceleration produced is 𝛼 = 𝑇/𝐼.
Consider a force F acting on a body at a distance r from its centre of mass. Discuss how it can be divided into a combination of linear motion and rotational motion by considering a force and a couple individually and then adding them up. |
Rotational equilibrium:
A body is said to be in rotational equilibrium if the net torque acting on it is zero. Then the angular velocity is either zero or is constant.
E.g.: A ladder leans on a frictionless wall. Find the forces acting on the ladder due to the wall and the ground.
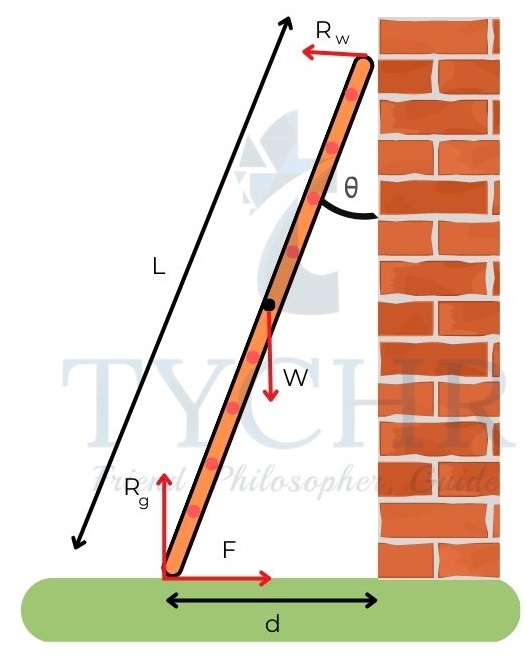
Answer. Balancing the forces,
Vertical: Rg=W
Horizontal: RW=F
The ladder is in rotational equilibrium. So, the torques should be balanced about any point.
Balancing torques about the bottom of ladder,
Torques in clockwise direction=Torques acting in counter clockwise direction
𝑊(𝐿/2) 𝑠𝑖𝑛𝜃 = 𝑅𝑤𝐿𝑐𝑜𝑠𝜃
𝑅𝑊 = 𝐹 = (𝑊/2)𝑡𝑎𝑛𝜃
Angular momentum:
Angular momentum of a body of moment of inertia I rotating at an angular velocity 𝜔 is 𝐼𝜔.
When no external torque acts on a system, the total angular momentum of the system remains constant. This is called law of conservation of angular momentum.
Rotational kinetic energy:
The kinetic energy due to rotation of a body of moment of inertia I rotating with an angular velocity 𝜔 is (1/2) 𝐼𝜔2.
Work done:
Work done on a body by a torque T that acts along an angular displacement 𝜃 is 𝑇𝜃 .
Rolling and sliding:
When a ball moves on a perfectly frictionless surface, it slides – there is no relation between angular motion and linear motion of the ball and both of them function independently.
When there is friction, the ball may roll – the point of contact of the ball with the surface remains at rest temporarily.
If the ball of radius r rolls with an angular velocity 𝜔 and has a linear velocity v, then
- v=𝜔r
- Every point on the surface of the ball has a tangential velocity and a velocity along the direction of linear motion, both magnitudes being equal to v.
- The top most part of the ball has a velocity 2v and the bottom most part remains at rest.
- The total kinetic energy of the ball is is (1/2)𝐼𝜔2 +(1/2)𝑚𝑣2.
E.g.: A solid ball, of radius of 45 mm, rolls down an inclined plane of length 2.5 m. The sphere takes a time of 6.0 s to roll down the plane. Assume that the ball does not slip.
The moment of inertia, I, of a solid ball of mass M and radius R is given by 𝐼 =(2/5)𝑀𝑅2
- Calculate the velocity of the sphere as it reaches the end of the plane.
- Calculate the angular velocity of the sphere as it reaches the end of the plane.
- Determine the angle of inclination of the plane.
- Comment on whether the assumption that the ball does not slip was appropriate in this instance.
Answer.
a) For the ball, the linear acceleration is 𝑎 = (2𝑠/𝑡2) =(2×2.5)/62 =0.14𝑚𝑠−2
So, the linear velocity of the ball at the end is 𝑣 = 𝑎𝑡 = 0.14 × 6 = 0.84𝑚𝑠−1.
b) The angular velocity is 𝜔 = 𝑣/𝑟 = 18.7𝑟𝑎𝑑𝑠−1
c) From law of conservation of energy,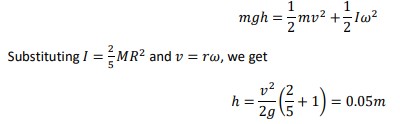
![]()
d) This angle is very small and there is no problem with assuming that the ball rolls without slipping.
Thermodynamics
Thermodynamics mainly focuses on extraction of work from heat.
Internal energy of the gas (U):
The total kinetic energy of a gas is the total kinetic energy of all molecules of the gas. It is assumed that there is no potential energy between gas molecules.
The internal energy of n moles of gas at a temperature T is (3/2)𝑛𝑅𝑇.
Work done by a gas (W):
Consider a gas contained in a cylinder at a pressure P undergoing a volume change ΔV. Then the work done by the gas is 𝑃ΔV.
Graphically, this is equal to the area under the curve in Pressure-Volume graph.
First law of thermodynamics:
The first law of thermodynamics states that energy can neither be created nor destroyed but can only be transformed from one form to another form.
𝑄 = Δ𝑈 + 𝑊
Sign convention:
Heat: Heat supplied to gas is positive.
Work: Work done by gas is positive when volume increases. Work done on the gas is the opposite. (Work in the equation of first law is work done by the gas)
Internal energy: Change in internal energy is positive if the temperature increases.
Types of processes:
Isobaric – constant pressure process:
Work done is 𝑃Δ𝑉.
For compression,
Isochoric – Constant volume process:
ΔV is zero. So, work done is zero.
First law equation reduces to 𝑄 = ΔU
When volume increases, the P-V graph is as follows
Isothermal – constant temperature process:
ΔT is zero. So, internal energy change is zero.
Δ𝑈 = 0, 𝑄 = Δ𝑊
An ideal gas follows 𝑃𝑉 = 𝑛𝑅T. So, in an isothermal process, PV=constant.
Adiabatic process:
No heat is exchanged. Process occurs in an isolated system.
Δ𝑄 = 0, Δ𝑈 + Δ𝑊 = 0
The gas follows the equation 𝑃𝑉𝛾= 𝑐𝑜𝑛𝑠𝑡𝑎𝑛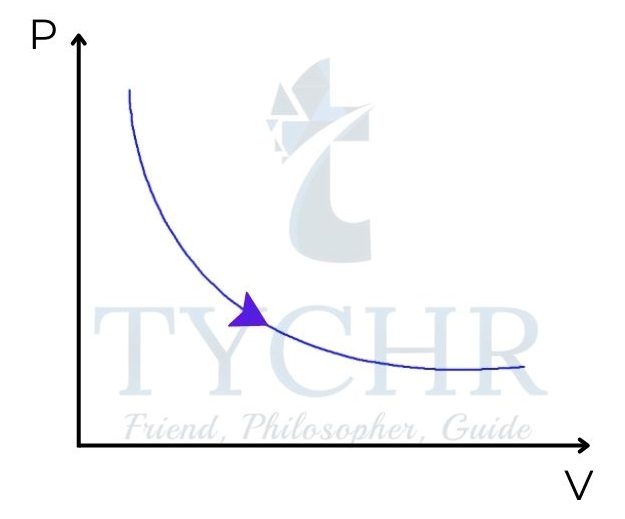
Cyclic processes:
A cyclic process is one in which the initial state is same as the final state. On a P-V diagram, it forms a closed loop.
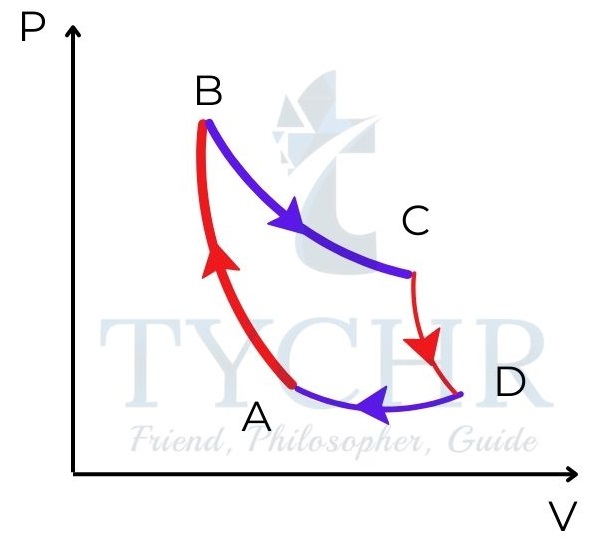
As the initial and final temperatures are same, the net change in internal energy is zero. These type of processes occur mostly in heat engines where heat is converted to work.
Heat engine:
A heat engine generally involves four processes.
- Heat intake
- Work output
- Heat rejection
- Work input
The net work done in a cyclic process is the area enclosed by the curve in P-V diagram.
The efficiency of a heat engine is given by the ratio of net work done by heat taken.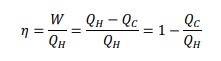
Carnot cycle:
A carnot cycle is the most efficient cycle which converts heat to work working between two fixed temperature reservoirs which provide and take heat during the cycle. In a carnot engine, the heat is exchanged at constant temperature and work exchange is done without any heat change. The P-V diagram looks like this.
The efficiency is 𝜂 = 1 − (𝑄𝑐/𝑄𝐻)= 1 − (𝑇𝐶/𝑇H)
Refrigerator:
When a carnot cycle is operated in reverse, it functions as a refrigerator – takes heat out from a low temperature reservoir and dumps it in a high temperature reservoir with work as input.
The performance of a refrigerator is given by 𝛽 = 𝑄𝐶 = 𝑇𝐶 𝑄𝐻 −𝑄𝐶 𝑇𝐻 −𝑇𝐶
E.g.: A quantity of an ideal gas is used as the working substance of a heat engine. The cycle of operation of the engine is shown in the p-V graph opposite. Change CA is isothermal. The temperature of the gas at A is 300 K.
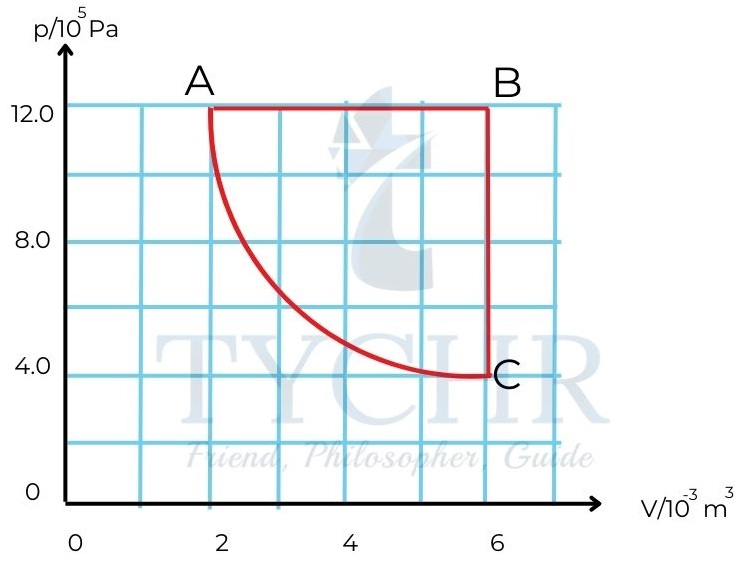
a) During the change AB the change in internal energy of the gas is 7.2 kJ.
(i) Calculate the temperature, at B, of the gas.
(ii) Determine the amount of energy transferred during change AB.
b) State why, for the change BC, the change in the internal energy of the gas is numerically the same as that in AB.
c) Calculate:
i) the net work done in one cycle
ii) the efficiency.
Answer.
a)
i) For an ideal gas at constant pressure,
V1/T1 = V2/T2
ii) 𝑊 = 𝑃Δ𝑉 = 12.0 × 105 × (6 − 2) × 10−3 = 4.8𝑘J
The increase in internal energy is 7.2kJ. So, the total energy supplied is 𝑊 + Δ𝑈 = 12.0𝑘J
b) The internal energy along AC does not change as ther is no change in temperature. In a cyclic process, the net internal change is zero. So, the internal change BC is same in magnitude to that of AB.
c)
i) The net work done is the area enclosed in the graph. From the graph, this is equal to 200J.
ii) Second law of thermodynamics:
𝜂 =𝑊/𝑄=2.8/12= 0.23
It is not possible to develop a heat engine that converts heat completely to work.
The above statement is the Kelvin-Planck statement of second law states:
It is not possible to develop a heat engine that converts heat completely to work.
It is impossible for heat to be transferred from a cold body to a hot body without any work being done.
The Clausius statement of the law is:
It is impossible for heat to be transferred from a cold body to a hot body without any work being done.
Entropy:
Entropy is the order of randomness of a system.
The increase in entropy of a system when Q amount of heat flows into it at a constant temperature T is 𝑄/𝑇.
Second law in terms of entropy:
The entropy of a closed system either increases or remains constant in a cyclic process.
Fluids and their dynamics
Fluids take the shape of a container and have the ability to flow. Gases and liquids are collectively called fluids.
Fluid statics
Density:
Density is the mass per unit volume.
𝜌 =𝑚/V
Pressure:
Pressure is the force acting per unit area.
Pressure is a scalar and is same in all directions at a point.
If the force acting on a surface of area A is F, then the average pressure at that point is F/A.
In a liquid of density whose pressure at the surface is P0, the pressure at a point h distance below the surface is 𝑃0 + 𝜌𝑔ℎ.
Pascal’s principle:
The pressure applied at one point in an enclosed point under equilibrium conditions is equally transmitted to all points in the fluid.
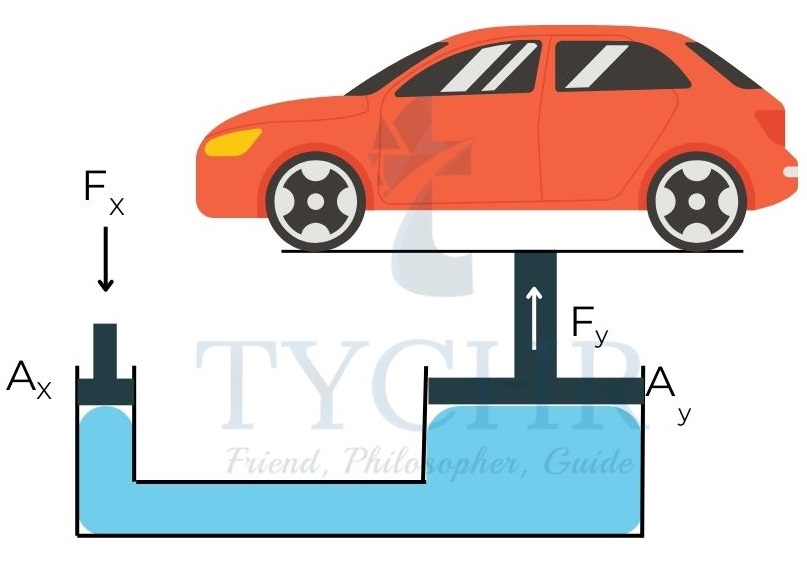
Consider the situation above. The pressure at the left end is 𝐹𝑥/𝐴𝑥. This is equal to the pressure on the right end 𝐹y/𝐴y. This gives:
𝐹𝑥=(𝐴𝑥𝐹y)/𝐴y
Varying the ratio , we can lift the load with a small force on the left.
Archimedes’ principle:
The buoyancy acting on an object immersed in a fluid is equal to the weight of fluid displaced by the object.
𝐵 = 𝑉𝜌𝑔
V is the volume of the object and is the density of fluid.
E.g.: The density of water is 103𝑘𝑔𝑚−3 and that of iron is 7.8 × 103𝑘𝑔𝑚−3. Calculate the force required to lift a 60kg ball from water.
Answer. The F.B.D of the ball is as follows.
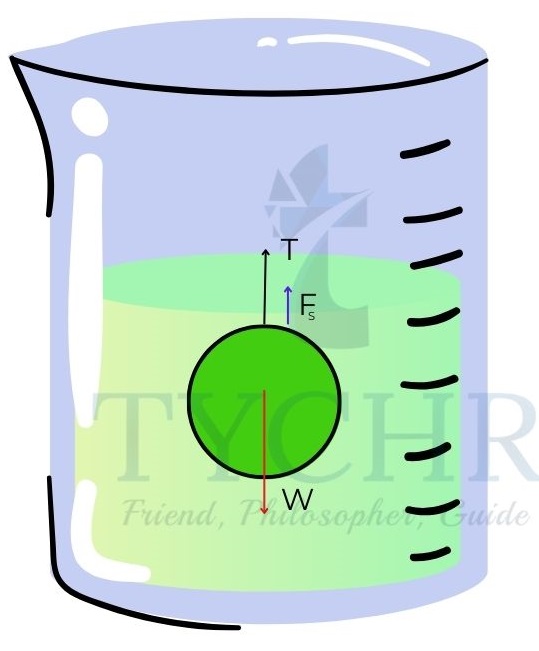
𝐹𝐵 + 𝑇 = 𝑊 = 60 × 9.8 = 588𝑁
Fluid dynamics
Streamlined flow:
In a streamlined flow, the motion of one particle passing through a point is similar to the motion of all points passing through that point. This is also called laminar flow.
The continuity equation:
It is applicable for incompressible liquids only. It is based on the fact that the mass of fluid entering is equal to the mass leaving.
The volume flow rate is constant throughout the flow.
At cross sections 1 and 2 of a flow,
𝐴1𝑣1 = 𝐴2𝑣2
Bernoulli’s equation:
(1/2)𝜌𝑣2 + 𝜌𝑔ℎ + 𝑃 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛
Applications of Bernoulli’s equation:
Pitot static tubes: These tubes are used to measure the velocity of a fluid. Two tubes – static and pitot tubes measure the static and dynamic pressure of the fluid. The velocity of the fluid is determined by 𝑣 = √2𝑔(ℎ𝑦 − ℎ𝑠).
E.g.: Consider a cylindrical container of uniform area A containing a liquid up to a height H. A small orifice is made at the bottom of the container. Find the velocity of ejected stream from the orifice.
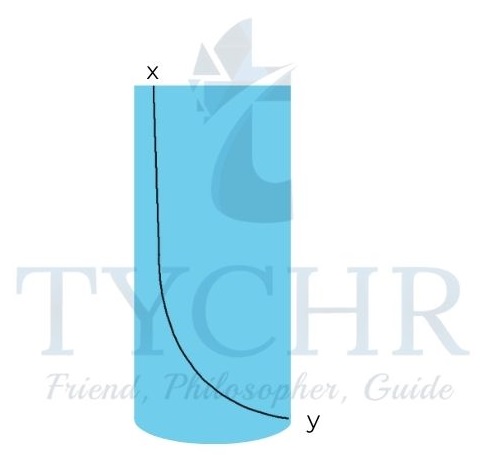
Answer. The orifice is assumed to be sufficiently small so that the velocity of surface of water is zero. The atmospheric pressure is P0.
Applying Bernoulli’s principle at the top and at the orifice,
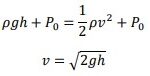
Viscosity of fluid:
Viscosity impedes the relative motion between layers of fluids.
It is measured in terms of coefficient of viscosity (𝜂).
In a river-like flow, the bottom-most layer remains at rest with the bed while the top most layer has highest velocity.
Consider two parallel plates of area A separated by a fluid of coefficient of viscosity 𝜂 by a distance h. The force required to move the upper plate with a velocity v is 𝜂𝐴(𝑣/L).
Viscosity of liquids decrease with temperature while that of gases increase with temperature.
Stokes law:
When a sphere of radius r falls through a fluid of coefficient of viscosity at a velocity v, the viscous force acting on it is 6𝜋𝜂𝑟𝑣.
The terminal velocity of a ball whose density is falling through a fluid of density 𝜌 is 𝑣𝑡 =(2𝑟2𝑔(𝜎−𝜌))/9𝜂.
Turbulent flow:
Reynolds number of a fluid flow is 𝑅𝑒 =𝑣𝑟𝜌/𝜂. Here r is the radius of pipe.
It is a dimensionless number and marks the transition between laminar and turbulent flow.
If the Reynolds number is greater than 2000, then the flow is considered to be turbulent.
Forced vibrations and resonance
Damped harmonic motion:
In the modelling of loaded spring and pendulum motion in previous chapters, it is assumed that no dissipative forces act on it.
The dissipative forces that act in real life mostly are of the form 𝐹 = −𝑏𝑣.
The equilibrium condition of such an object gives the following equation:
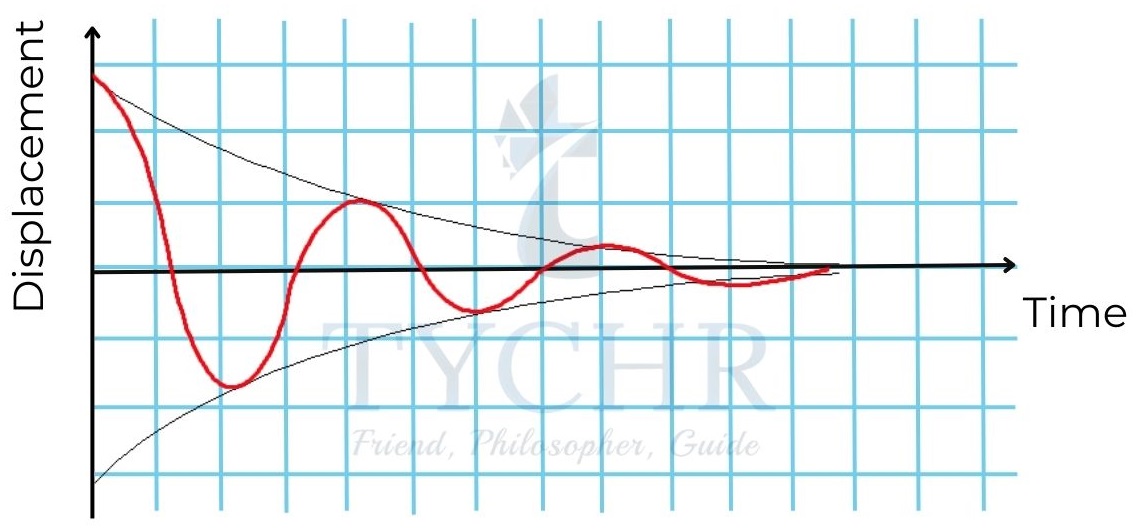
The amplitude decreases exponentially with time. The above shown example is under damped – the value of bm is small.
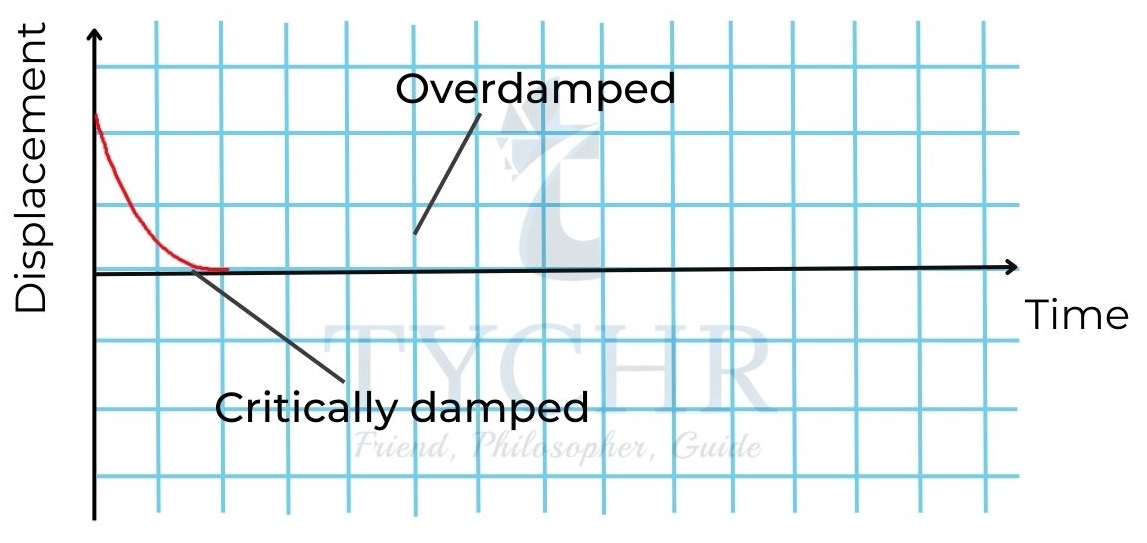
The damping is said to be critical, when the object reaches equilibrium position and stops at that position. It is said to be over damped when the object does not reach equilibrium position at all.
The quality factor:
The quality factor (Q) is a measure of the number of oscillations the system can perform before it runs out of energy. For a large number of oscillations, this is approximately equal to the number of oscillations performed by the system.
𝑄 =2𝜋(𝑒𝑛𝑒𝑟𝑔𝑦 𝑠𝑡𝑜𝑟𝑒𝑑)/𝑒𝑛𝑒𝑟𝑔𝑦 𝑙𝑜𝑠𝑡 𝑝𝑒𝑟 𝑐𝑦𝑐𝑙e
If Q is high, then the system can perform large number of oscillations without much loss of energy in each cycle.
E.g.: An electrical pendulum clock has a period of 1.0 s. An electrical power supply of 25 mW maintains its constant amplitude. As the pendulum passes its equilibrium position it has kinetic energy of 40 mJ.
Calculate the Q factor for the pendulum clock.
Answer. The pendulum has a frequency of 1.0 Hz. As it is storing 40 mJ, the rate of energy supplied must equal the rate at which energy is lost i.e., the power is supplied at a rate of 25mW.![]()
Forced vibration:
When an oscillating system is subjected to a sinusoidal force, then the system oscillates with the frequency of force rather than its natural frequency.
Resonance:
When the driving frequency of the force matches with the natural frequency of the system, then the amplitude of vibration reaches a maximum. This is called resonance.
Effect of damping:
In a lightly damped system, the resonant frequency is almost the same as that of natural frequency. If the system is heavily damped, the resonant frequency is less than natural frequency.
Q factor for a forced, damped oscillator is:
𝑄 = 2𝜋 × 𝑟𝑒𝑠𝑜𝑛𝑎𝑛𝑡 𝑓𝑟𝑒𝑞𝑢𝑒𝑛𝑐𝑦 × (𝑒𝑛𝑒𝑟𝑔𝑦 𝑠𝑡𝑜𝑟𝑒𝑑/𝑒𝑛𝑒𝑟𝑔𝑦 𝑙𝑜𝑠𝑡 )
Resonance curves with various Q factors:
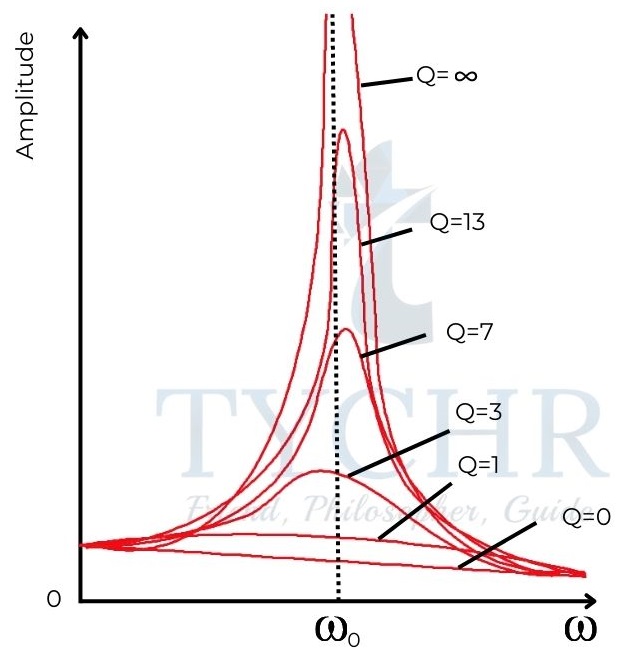
Phase difference between driver and driven:
When the system is in resonance, the driver leads the driven by 𝜋/2 phase.
At a frequency less than resonant frequency, the driver and driven are in phase.
At a frequency greater than resonant frequency, the difference in phase difference is 𝜋.
Electrical resonance:
A resistor, conductor and an inductor connected in series forms a damped oscillating system. The resonant frequency depends on the conductance and this can be used to electric signals of certain frequency.

