Measurements And Uncertainties Theory Notes
Quantities and units
Physical quantities:
- Quantities that can be measured are called physical quantities.
Fundamental quantities:
- Fundamental quantities are basic quantities such that all other quantities can be expressed in terms of them.
- There are seven fundamental quantities-mass, length, time, electric current, temperature, amount of substance and luminous intensity.
Derived quantities:
- These quantities are derived from fundamental quantities and other derived quantities. Consider density. It is derived from mass and volume which in turn is derived from length. So, density is a derived quantity.
Few quantities are defined below.
- Distance is used to define the position of different objects.
- Time is used to distinguish different events.
- Mass defines how much matter the object consists of.
- Volume is a measure of the amount of space taken up by the object.
- Density is the ratio of mass to the volume occupied by an object. This ratio is the same for objects made of the same material.
- Displacement is the distance moved in a particular direction. It defines the movement of an object.
- An angle is formed when two lines intersect. The angle can be changed by rotating a line about the vertex (the point of intersection).
Units:
Units are defined so that all quantities can be measured without ambiguity. The worldwide standard for units is SI-Système international d’unités. This system of units is agreed internationally to be used in science. Other units can also be used, but they have to be properly used in terms of SI units.
Fundamental units are units of fundamental physical quantities.
- Metre (m) is the SI unit of length. It is the distance travelled by light in vacuum during a time interval of 1/299792458 of a second.
- Kilogram (kg) is the SI unit of mass. It is equal to the mass of the international prototype of kilogram kept at the Bureau International des Poids et Mesures at Sèvres, near Paris.
- Second (s) is the SI unit of time. It is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom.
- Ampere (A) is the constant current which when maintained in two straight parallel conductors of infinite length and negligible cross section placed 1m apart in vacuum would produce a force of 2 × 107 N per metre of length.
- Kelvin (K) is the SI unit of temperature. It is the fraction 1/273.15 of thermodynamic temperature of triple point of water.
- Mole (mol) is the SI unit of amount of substance. It is the amount of substance of a system of a system that contains as many elementary entities as there are atoms in 0.012kg of carbon-12.
- Candela (cd) is the SI unit of luminous intensity. It is the luminous intensity in a given direction of a source that emits monochromatic radiation of frequency 540 × 1012 Hz and has a radiant intensity in that direction of 1/683 watt per steradian.
There are two supplementary units in SI system.
- Radian (rad) is the SI unit of angular measurement. It is the angle subtended at the centre by an arc of length equal to that of radius of circle.
- Steradian (sr) is the SI unit of solid angle and is a 3-D equivalent of radian which uses the concept of mapping a circle on a sphere.
Relating fundamental and derived units:
Derived quantities are to be written in terms of fundamental quantities and then units of corresponding fundamental quantities are related to the derived quantity.
Consider unit of force.![]() Now it is written in terms of mass, displacement and time. These are fundamental quantities. Therefore, the unit of force is 𝑘𝑔 × (1/𝑠) (𝑚/𝑠) = 𝑘𝑔𝑚𝑠−2 . This is commonly called newton.
Now it is written in terms of mass, displacement and time. These are fundamental quantities. Therefore, the unit of force is 𝑘𝑔 × (1/𝑠) (𝑚/𝑠) = 𝑘𝑔𝑚𝑠−2 . This is commonly called newton.
Significant figures:
The first non-zero digit from the left is the most significant digit.
Rules for using significant figures:
- A digit that is not zero is always significant.
- A zero occurring between two non-zero digits is significant.
- Zeroes without any preceding non-zero digits are not significant.
- Zeroes occurring to the right of decimal point are significant.
- If there is no decimal point, trailing zeroes are not significant.
Scientific notation:
To write a number in scientific notation, only a digit to the left of the decimal point is written to represent the number with power of tens.
E.g.: The speed of light is 299 792 458 ms-1. In scientific notation, this is rounded and written as 3×108 ms-1.
E.g.: Adding two numbers written in scientific notation,
1.40 × 106 + 3.5 × 105 = 1.40 × 106 + 0.35 × 106 = 1.75 × 106
E.g.: Multiplying two numbers,
3.7 × 105 × 2.1 × 108 = 7.77 × 1013
This has to be rounded to 7.8 × 1013.
Metric multipliers:
Powers of ten are abbreviated for easy representation of large and small numbers. These are prefixed to the units.
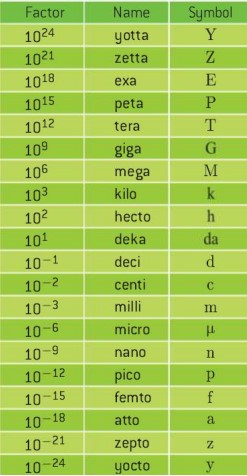
Order of magnitude:
The number rounded to the nearest power of ten is called order of magnitude.
Uncertainties and errors
When an experiment is performed, it is usually repeated a number of times and a number of observations are noted.
The observations are said to be precise if the observations are close to each other.
The observations are accurate if they are close to the actual value.
The difference in the observed value and actual value is called error.
Types of errors:
Random errors:
Random errors propagate due to various reasons. Most of the times, this reason is undetermined. The small variations in the readings are due to random errors. When random errors are small, the observations are precise.
Systematic errors:
Systematic errors are due to faulty instruments. When systematic errors are small, the measurement is accurate.
Expressing measurements and uncertainties:
To reduce errors, the mean of all measurements is taken. By doing this, the uncertainty due to random errors is minimised as the random errors cause the measurement to vary around the actual value.
Uncertainty is sometimes taken by conscience. Sometimes, it is the standard deviation of the observations. It is also taken as half the range of measurements. When digital scales are used, the uncertainty is the smallest scale division available.
Having determined the mean and uncertainty, the measurement is then expressed as
𝑚𝑒𝑎𝑛 ± 𝑢𝑛𝑐𝑒𝑟𝑡𝑎𝑖𝑛𝑡𝑦
E.g.: In measuring the angle of refraction for a constant angle of incidence, the following results were obtained.
45˚, 47˚, 46˚, 45˚, 44˚
How should the angle of refraction be expressed?
The mean of these values is 45.4˚ and the range is 3˚. Half of the range is 1.5˚. Since the precision of the protractor is 1˚, the measurement and uncertainty have to be expressed in integer multiples of it. The measurement has to be rounded off to 45˚ and without minimising uncertainty, it has to be 2˚.
So, the result should be expressed as 45˚ ± 2˚.
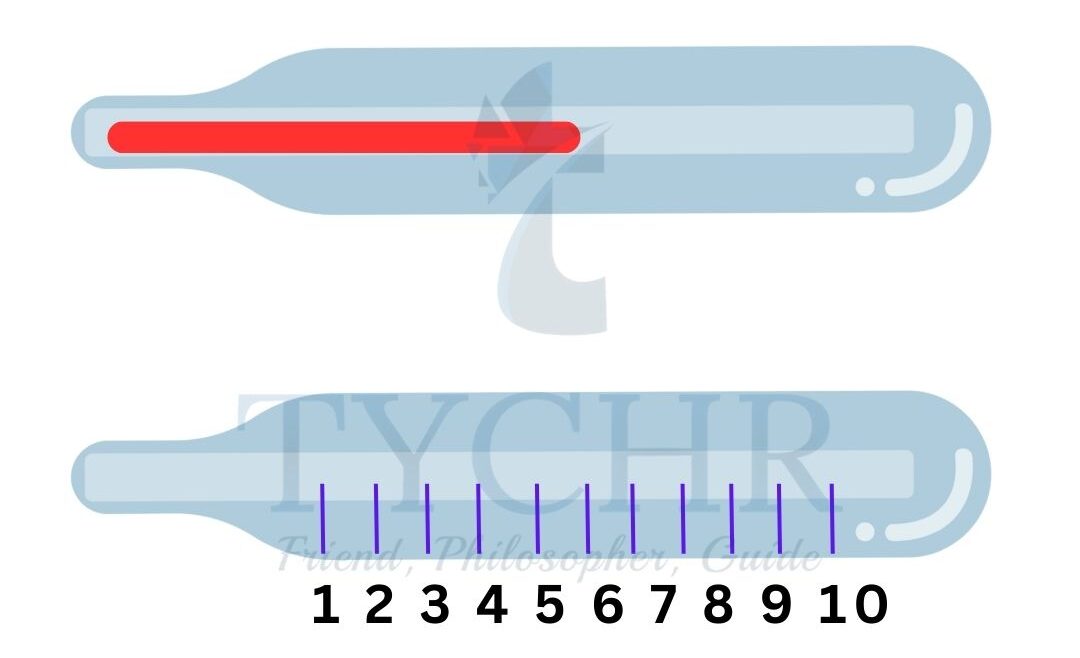
E.g.: The diagram below shows the meniscus of mercury in a thermometer. Express the temperature and uncertainty to appropriate numbers of significant figures.
Ans. The scale is calibrated in degrees. But the calibration is clear. So, the uncertainty can be assumed to be 0.5˚. The meniscus is closer to 6˚. So, the temperature should be recorded as 6˚±0.5˚.
Graphs:
Graphs are very useful in realizing the trend of observations. Best fit curves are used to understand the relationship between quantities.
Error bars:
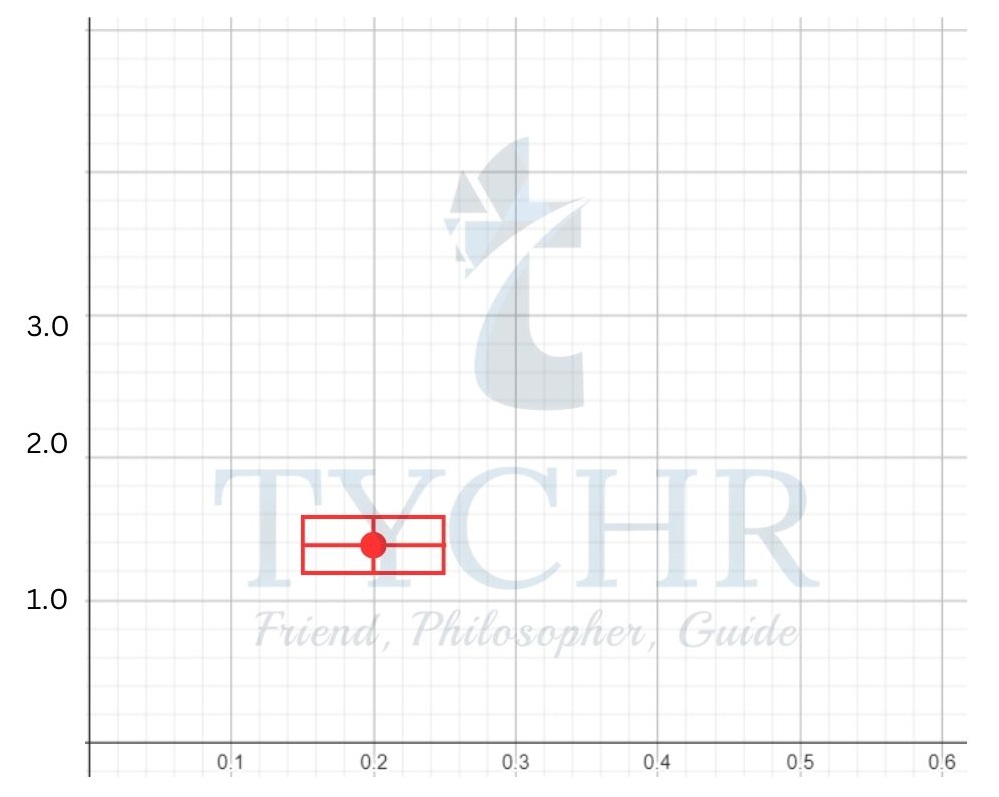
Suppose that the velocity of a body is being measured with respect to time. Suppose at a time of (0.2 土 0.05) s, the speed of object is (1.2 土 0.2) ms-1. This is represented in graph as
The rectangle is called zone of uncertainty.
Uncertainties in gradients:
To find the uncertainty in gradient, steepest and shallowest lines passing through all the error bars are drawn. Then, the uncertainty is half the range of gradients.
Linearizing relationships:
If the relationship between two quantities (A and B) is linear, they can be directly plotted and the relationship between the quantities can be understood.
If the relationship between them is known to be of the form B=KAn. Then the graph can be plotted between B and An. This gives a linear graph whose gradient is K.
Another method is to plot the graph between logB and logA. This gives a linear plot with gradient n and intercept logK.
If the quantities are related exponentially such as B=KemA, they are plotted between logarithms of B with base e and A. This then gives a linear plot with gradient m and intercept lnK.
If the relationship between quantities is unknown, we assume that the quantities are related as B=KAn and proceed with graphing.
Absolute and fractional uncertainties:
The uncertainty of the form ∆x is absolute uncertainty. Fractional uncertainty is ∆𝑥/𝑥.
If two quantities A and B with uncertainties ∆A and ∆B are to be added or subtracted, then the absolute uncertainty of the resulting quantity is ∆A+∆B.
If the quantities are to be multiplied or divided, then the fractional uncertainty of resulting quantity is .
If a quantity is to be raised to a power n, then the fractional uncertainty in resulting quantity is n times the fractional uncertainty of the quantity.
E.g.: If the length of a cube is 5.00 土 0.01 m, find the uncertainty in volume.
Ans. Fractional uncertainty in length is0.01/5 = 0.002.
Volume of cube is 53=125m3.
Fractional uncertainty in volume = fractional uncertainty in length = 3 x 0.002 = 0.006
Absolute uncertainty in volume = 0.006 x 125 = 0.75.
So, the volume is 125 土 0.75 m3.
E.g.: The distance covered in a running track is 400 土 1 m. If a person runs around the track 4 times, find the distance covered and uncertainty.
Ans. The distance covered is 400 x 4 = 1600 m.
It is equivalent to adding the distance 4 times. So, the absolute uncertainty gets added 4 times.
Uncertainty = 4 x 1=4m.
So, the distance covered is 400 x 4 = 1600 m.

Vectors and scalars
Scalars are quantities that have only magnitude. Distance and time fall in this category. The operations involving scalars are dealt using rules of algebra.
Vectors have magnitude and direction. Displacement is the vector equivalent of distance. Vectors are represented with a line and arrow. The arrow representing direction and the line representing the magnitude of the quantity to scale.
Addition of vectors:
Graphical approach:
The two vectors are drawn such that they form adjacent sides of a parallelogram. A parallelogram is completed by drawing identical vectors opposite to the original vectors. The diagonal originating from the origin is the resultant vector in both magnitude and direction.
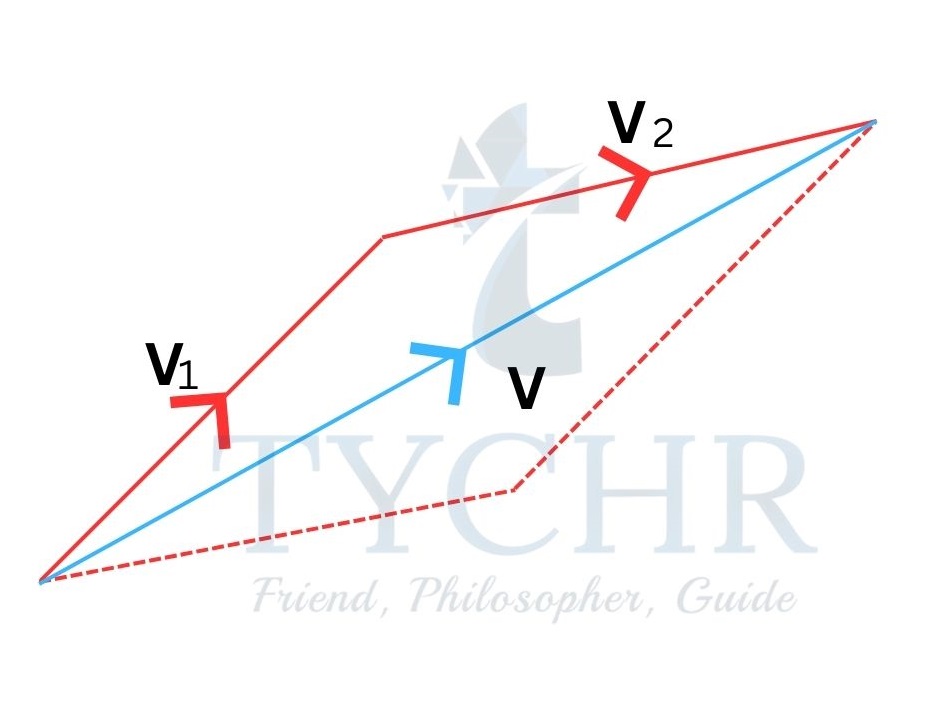
V=V1+V2
Analytical approach:
Adding vectors at right angles:
Two vectors at right angles can be added by using Pythagoras theorem.
The magnitude of resultant vector is √𝑉1 2 + 𝑉22.
The resultant vector makes an angle tan−1 (V1/V2 )with V1.
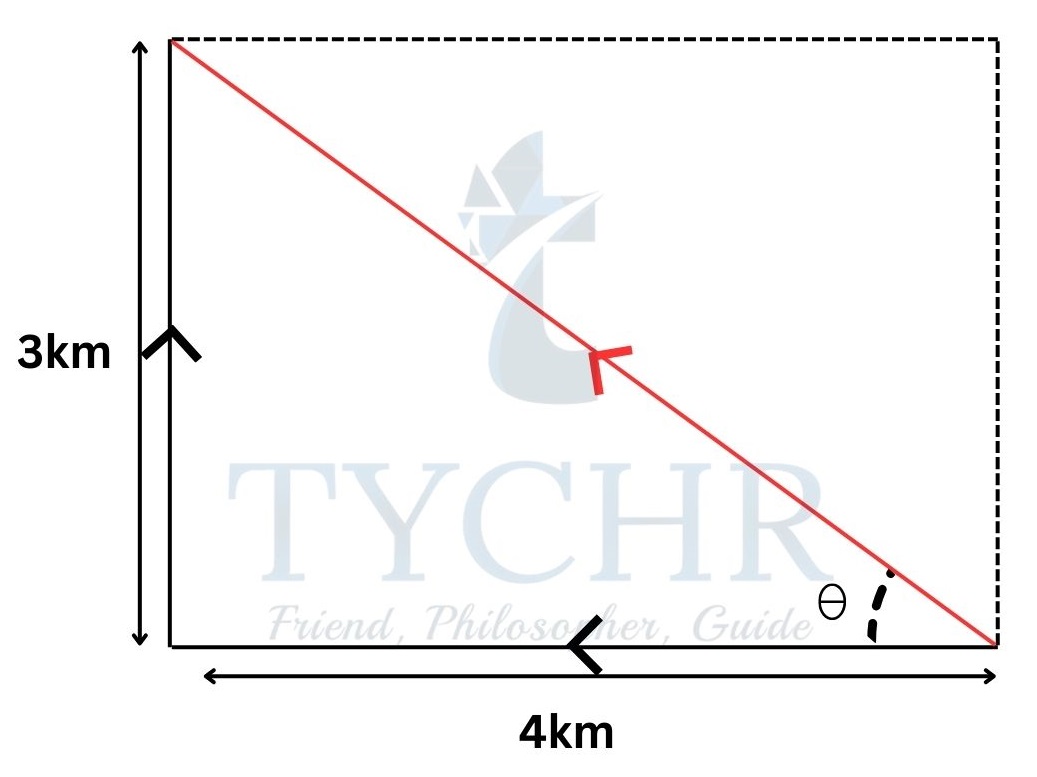
E.g.: A walker walks 4km due west and 3km due north. How far is the walker from his starting point?
Ans. Resultant = √42+32=5
Angle = tan−1(3/4)= 36.9˚
Resolving vectors:
Every vector can be resolved into a number of vectors such that when those vectors are added, the result in the original vector.
Generally, the vectors are resolved into perpendicular components.
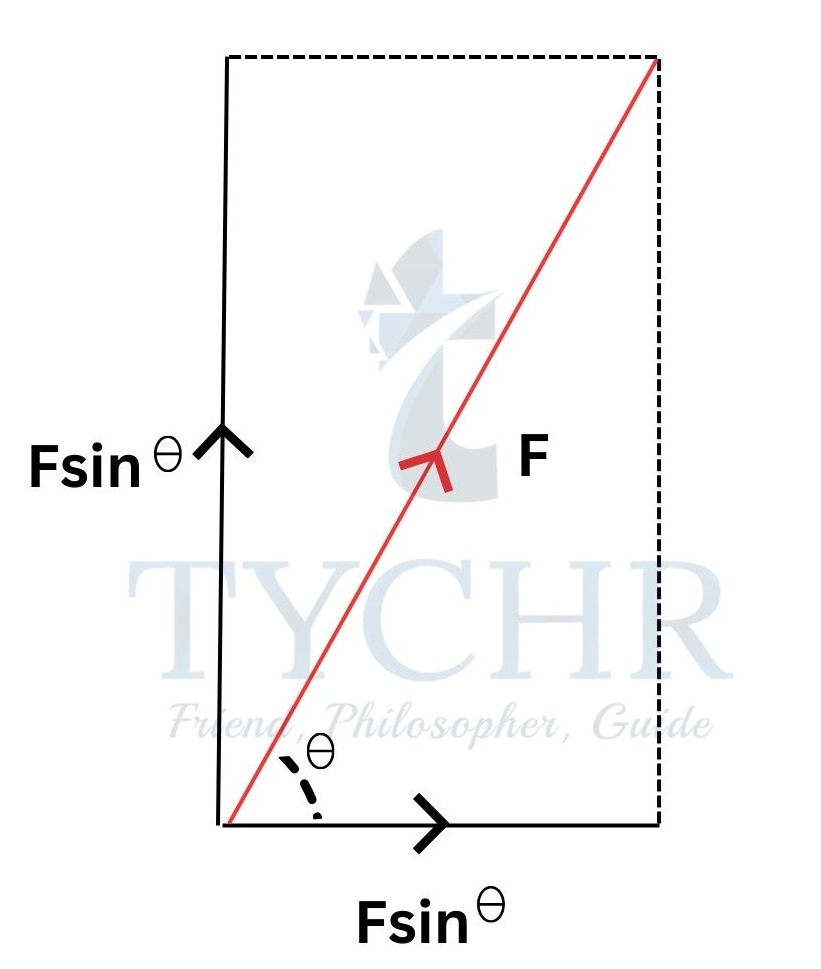
Here the force F is resolved into horizontal component Fcosθ and vertical component Fsinθ.
E.g.: An ice hockey puck is struck at angle of 60˚ to the longer side of rink. It then moves with a constant speed of 40ms-1. Find the distance travelled parallel and perpendicular to the longer side in the next 0.5s.
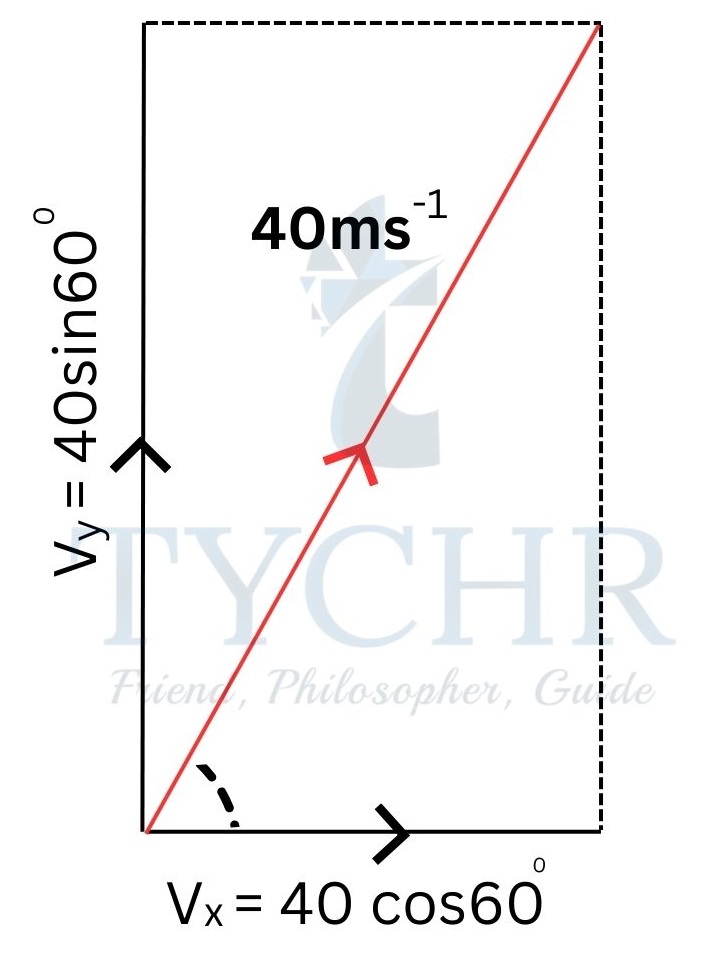
Horizontal component of velocity is 40cos60˚=20ms-1. So, the distance travelled in 0.5s is 20 x 0.5 = 10m.
Vertical component of velocity is 40sin60˚=34.6ms-1.
The distance travelled in vertical direction is 34.6 x 0.5 = 17.3m.
Adding vectors that are not at right angles:
The vectors are to be resolved into perpendicular components. Adding all the components in a direction gives the resultant component in that direction. The resultant components in two directions can be added using Pythagoras theorem.
Suppose vectors V1 and V2 making angles θ1 and θ2 are to be added.
Resultant horizontal component Vx = V1cosθ1 + V2cosθ2
Resultant vertical component Vx = V1sinθ1 + V2sinθ2
Magnitude of resultant vector =√𝑉𝑥2+𝑉𝑦2
And the angle made by resultant vector with horizontal is tan−1(𝑉𝑥/𝑉𝑦).
E.g.: Two magnetic fields have strengths 200mT and 150mT and act at 27˚ to one another. Find the resulting magnetic field.
Ans.
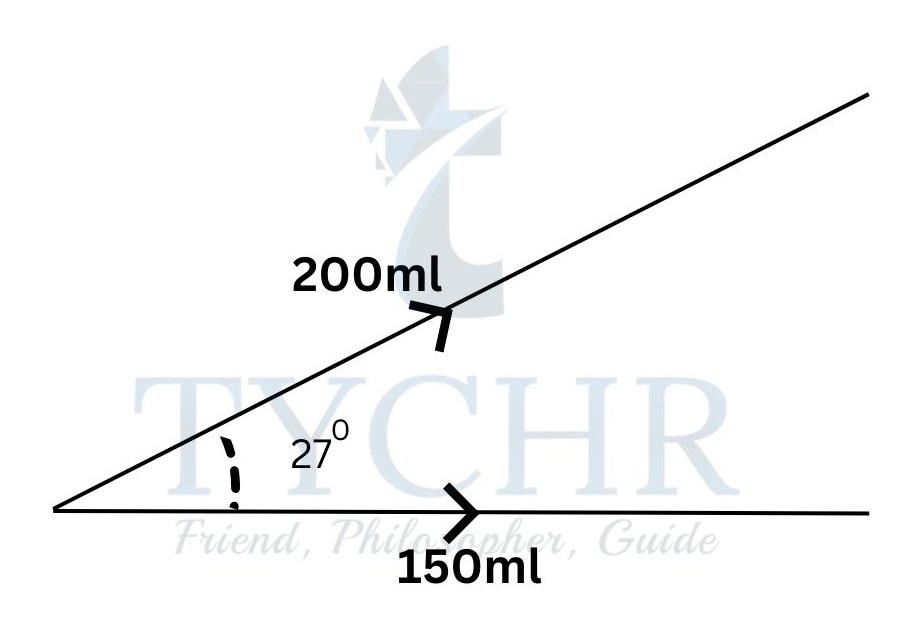
The total horizontal component is 150cos0 + 200cos27˚ = 328.2mT
Total vertical component is 150sin0 + 200sin27˚ = 90.8mT
Resultant field strength = √328.22 + 90.82 = 340mT
The resultant field makes an angle of tan−1(90.8/328.2)= 15˚ with the 150mT field.
Subtracting vectors:
The vector to be subtracted is written as a negative of the vector and added to the other vector. Making the vector negative is same as changing its direction by 180˚.
