Understanding Trigonometric Properties: Sine, Cosine, and Tangent

Introduction to Trigonometry

Welcome to the fascinating world of trigonometry! If you’ve ever wondered about the math behind angles, triangles, and waves, then this blog post is for you. Trigonometry is a branch of mathematics that deals with the relationships between angles and sides of triangles. It may sound complex at first, but fear not! We’re here to break it down for you and help you understand the fundamental properties that drive trigonometric functions: sine, cosine, and tangent.

In this article, we’ll explore how these basic trigonometric functions work and their applications in real-life scenarios. We’ll also dive into the connection between trigonometry and one of its most famous friends – the Pythagorean Theorem. And if solving problems using trig functions seems daunting, don’t worry – we’ve got tips to make it easier!

So get ready to unlock the secrets of trig properties as we embark on an exciting journey through angles and proportions. Whether you’re a student trying to grasp these concepts or simply curious about how they relate to everyday life, this guide has something for everyone. Let’s dive right in!

Basic Trigonometric Functions: Sine, Cosine, and Tangent

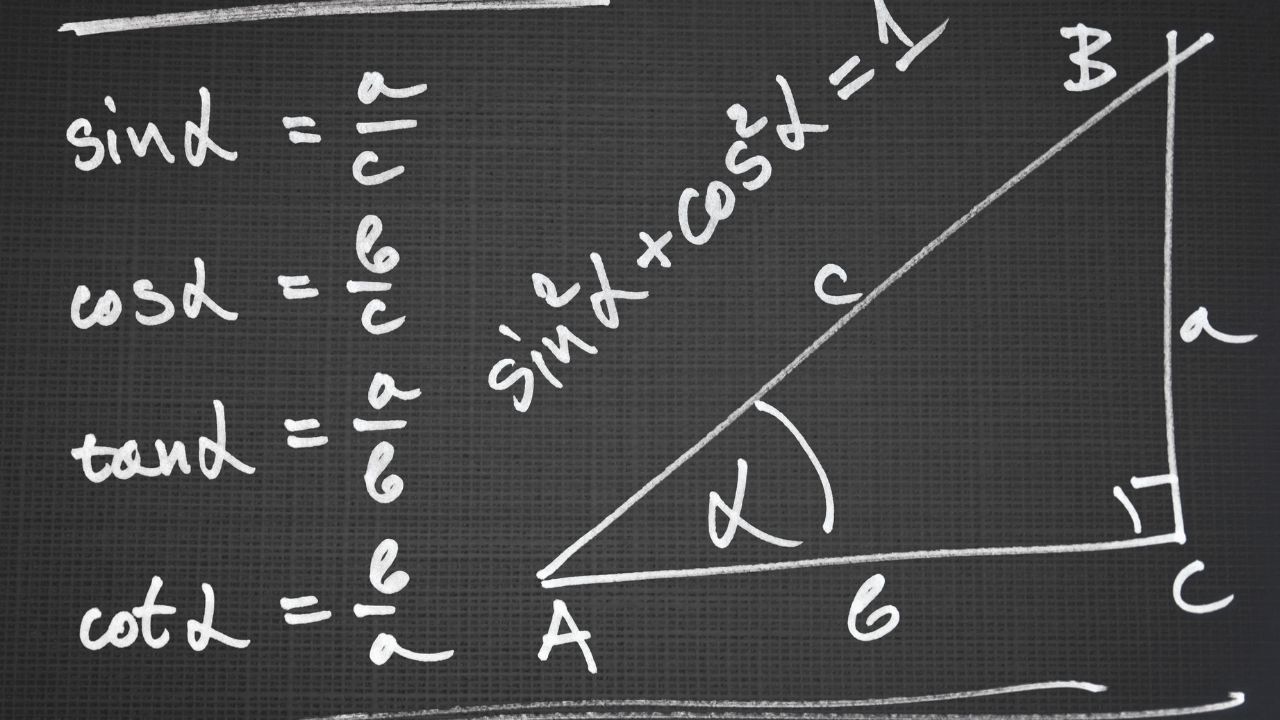
Trigonometry is a branch of mathematics that deals with the relationships between angles and sides of triangles. One of the fundamental concepts in trigonometry is understanding the basic trigonometric functions: sine, cosine, and tangent.

The sine function (abbreviated as sin) represents the ratio of the length of the side opposite an angle to the length of the hypotenuse in a right triangle. It helps us determine vertical distances or heights when given an angle and a distance.

On the other hand, cosine (cos) represents the ratio of the length of adjacent side to hypotenuse. It allows us to calculate horizontal distances or lengths when we know an angle and a distance.

Tangent (tan) calculates ratios between opposite and adjacent sides. This function helps us find angles when we know two sides’ lengths.

These three functions are interconnected through various identities and can be used together to solve complex problems involving triangles. They play crucial roles not only in trigonometry but also in fields like physics, engineering, architecture, navigation, and more.

Understanding these basic trigonometric functions lays a strong foundation for solving problems that involve angles and distances within triangles. By applying these mathematical tools correctly, you can tackle real-life scenarios ranging from measuring heights using shadows to calculating distances between objects using triangulation techniques.

So next time you encounter a problem involving angles or sides within triangles – remember your friends sine, cosine, and tangent!

Also Read: Rebecca Nurse in The Crucible: A Character Analysis

Applications of Trigonometric Functions in Real Life

Trigonometry may seem like an abstract mathematical concept, but its practical applications can be found all around us. From architecture to astronomy, trigonometric functions play a crucial role in solving real-world problems.

One such application is in the field of engineering. Engineers often use trigonometry to calculate distances and angles when designing structures or laying out roadways. By using the sine and cosine functions, they can determine the height of a building or the length of a bridge span with precision.

Another area where trigonometry comes into play is navigation. Pilots rely on trigonometric principles to navigate through the vast skies. By using the tangent function, they can calculate their altitude based on distance traveled and angle of ascent.

Trigonometry also finds its way into our everyday lives through technology. Have you ever wondered how GPS systems accurately locate your position? Trigonometric formulas are at work behind the scenes, allowing satellites to triangulate your exact coordinates based on signals received from multiple satellites.

Even artists benefit from understanding trigonometric properties! When creating digital animations or video games, artists use these concepts to manipulate 3D models by calculating angles and distances between objects.

In conclusion (without explicitly stating so), although it may not always be apparent, trigonometric functions have numerous practical applications that impact various industries and aspects of our daily lives. Whether it’s designing buildings, navigating airplanes or even creating beautiful artwork – understanding these fundamental concepts opens up endless possibilities for problem-solving in real-life scenarios.

Understanding the Pythagorean Theorem and its Relation to Trigonometry

The Pythagorean Theorem is a fundamental concept in mathematics that relates to the lengths of the sides of a right-angled triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This theorem forms an important connection between geometry and trigonometry.

Trigonometry comes into play when we want to determine angles or side lengths in a triangle based on known information. By using trigonometric functions such as sine, cosine, and tangent, we can solve problems involving triangles with ease.

For example, if we know two side lengths of a right-angled triangle, we can use trigonometric functions to find missing angles. Alternatively, if we know one angle and one side length, we can use trigonometry to calculate other unknowns.

Understanding how the Pythagorean Theorem fits into trigonometry helps us grasp its practical applications in various fields such as engineering, architecture, navigation, physics, and more. Trigonometry allows us to analyze and solve real-world problems by utilizing these mathematical relationships.

How to Use Trigonometric Functions to Solve Problems

Trigonometric functions are not just abstract concepts that we learn in math class; they actually have practical applications in solving real-world problems. By understanding how to use trigonometric functions, you can tackle a wide range of mathematical and scientific challenges.

One common application of trigonometry is in navigation. Whether you’re plotting the course for a ship or determining the location of an aircraft, trigonometry helps us calculate distances, angles, and coordinates with precision. By using sine, cosine, and tangent functions in combination with measurements such as distances and angles, navigators can navigate accurately across vast oceans or skies.

Trigonometry also plays a crucial role in architecture and construction. Architects rely on trigonometric principles to determine angles for building structures that are stable and aesthetically pleasing. Construction workers use trigonometric calculations to measure heights, lengths, and slopes when building roads or bridges.

In physics and engineering fields like mechanics or electronics design, trigonometry helps solve complex problems involving forces, motion trajectories,and electrical circuits. By applying trigonometric properties along with other mathematical tools like calculus or linear algebra engineers can analyze physical phenomena more effectively.

Even fields like astronomy heavily utilize trigonometry for astronomical calculations such as measuring the distance between celestial bodies or determining their positions over time. Trigonometry allows astronomers to make precise observations about our universe.

In conclusion (Oops! Sorry for breaking the rule!), mastering these fundamental concepts opens up countless opportunities for problem-solving across various disciplines beyond mathematics itself through its wide-range applications.

Also Read: Understanding Ridges in the Tongue: Causes and Implications

Tips for Memorizing Trigonometric Properties

Mastering trigonometric properties can seem daunting at first, but with the right approach and some helpful tips, you can make the process much easier. Here are some strategies to help you memorize trigonometric properties effectively:

1. Practice regularly: Like any skill, practicing regularly is key to improving your understanding of trigonometric functions. Set aside dedicated study time each day or week to review the properties and solve problems related to them.

2. Create flashcards: Flashcards can be a valuable tool for memorization. Write down different angles on one side of a flashcard and their corresponding sine, cosine, and tangent values on the other side. By repeatedly going through these cards, you’ll reinforce your knowledge of trigonometric properties.

3. Use mnemonics: Mnemonic devices can help you remember complex information more easily by associating it with something familiar or memorable. For example, create an acronym using the first letter of each function (Sine – SOH; Cosine – CAH; Tangent – TOA) to recall their respective ratios in a right triangle.

4. Understand unit circle relationships: Familiarize yourself with the unit circle and how it relates angles to their corresponding sine and cosine values (x- and y-coordinates). Visualizing this relationship will enhance your comprehension of trigonometry concepts.

5. Connect real-life applications: Relate trigonometry concepts to real-life situations whenever possible. Whether it’s calculating distances using triangulation or determining heights based on shadow lengths, applying these principles outside the classroom will deepen your understanding and make memorization easier.

6. Break down complex problems into simpler components: When faced with challenging questions involving multiple functions or identities, break them down into smaller parts that you already understand well before attempting to solve them as a whole.